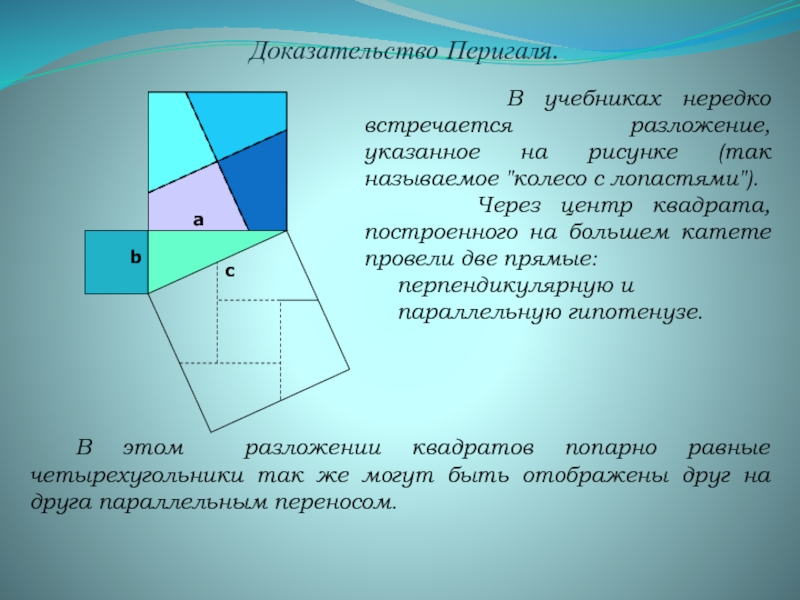
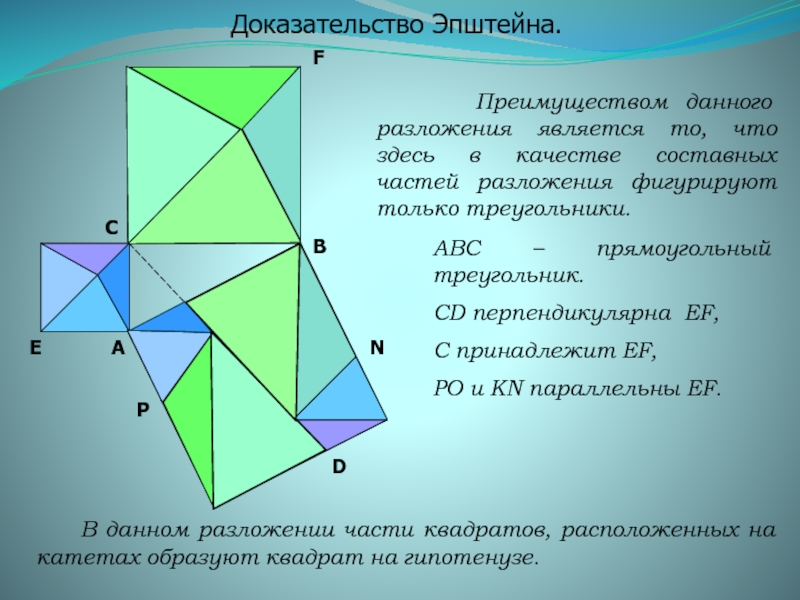
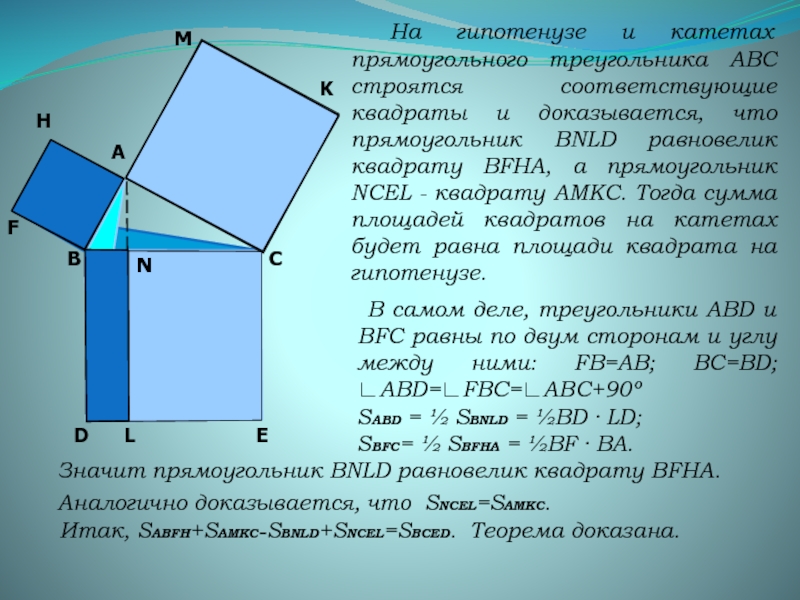
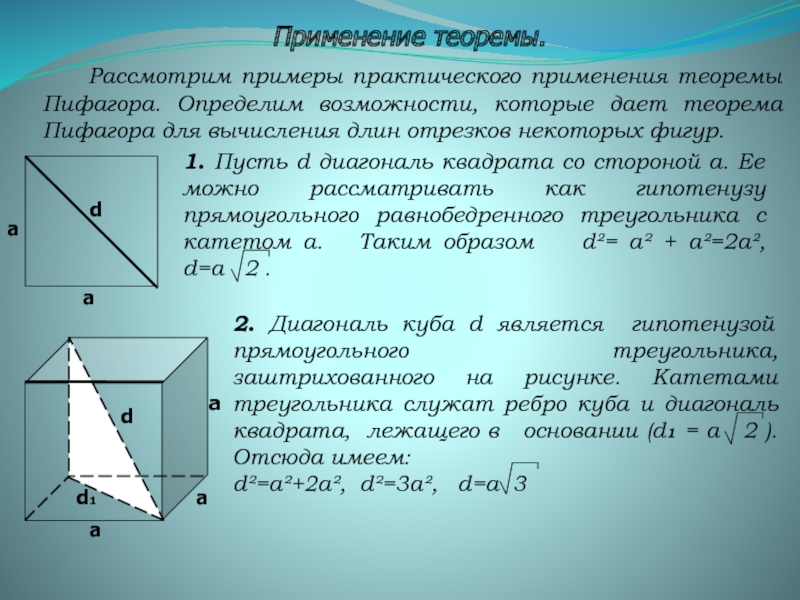
Теорема Пифагора, различные способы ее доказательства

теорема Пифагора... Иоганн Кеплер.
Трудно найти человека, у которого имя Пифагора не

ассоциировалось бы с теоремой Пифагора. Без преувеличения можно сказать, что это самая известная теорема геометрии, так как о ней знает подавляющее большинство населения планеты. Причин такой популярности три: простота, красота, широчайшая применимость.
В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу. Существует около 500 различных доказательств этой теоремы.

Пифагор Самосский.    

(Pythagoras of Samos)
570 – 475г до н.э.
Великий ученый Пифагор родился окол 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням.
Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам. У своего первого учителя Гермодамаса Пифагор получает знания основ музыки и живописи. По совету своего учителя Пифагор решает продолжить свое образование в Египте.
Учеба Пифагора в Египте способствует тому, что он сделался одним из самых образованных людей своего времени.

до Пифагора:
В настоящее время известно, что эта

теорема не была открыта Пифагором. Однако полагают, что Пифагор первым дал ее полноценное доказательство.

построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на

его катетах."
Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. Достаточно просто посмотреть на мозаику равнобедренных прямоугольных

треугольников, чтобы убедиться в справедливости теоремы. Например, для ∆ ABC: квадраты, построенные на катетах АВ и ВС, содержат по 2 исходных треугольника, а квадрат, построенный на гипотенузе АС — 4 таких же треугольника. Теорема доказана.

помещен чертеж с характерным

для индийских доказательств словом «смотри!»

Как мы видим, если в квадрате со стороной с два заштрихованных треугольника отрезать и приложить гипотенузами к двум другим гипотенузам, то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и b, т.е. с²= а² +b².

b²

a²

доказательств теоремы Пифагора, в которых квадраты, построенные на катетах и

на гипотенузе, разрезаются так, что каждой части квадрата, построенного на гипотенузе, соответствует часть одного из квадратов, построенных на катетах. Во всех этих случаях для понимания доказательства достаточно одного взгляда на чертеж; рассуждение здесь может быть ограничено единственным словом: "Смотри!", как это делалось в сочинениях древних индусских математиков.

помощью разбиения ан-Найризия – средневекового багдадского комментатора «Начал» Евклида.

Это разложение квадратов интересно тем, что его попарно равные части отображаются друг на друга параллельным переносом.

В этом разбиении квадрат, построенный на гипотенузе, разбит на 3 треугольника и 2 четырехугольника. Квадрат на большем катете разбит на 2 треугольника и 1 четырехугольник, а квадрат на меньшем – на 1 треугольник и 1 четырехугольник.

указанное на рисунке (так называемое "колесо с лопастями").

Через центр квадрата, построенного на большем катете провели две прямые:
перпендикулярную и
параллельную гипотенузе.

  В этом разложении квадратов попарно равные четырехугольники так же могут быть отображены друг на друга параллельным переносом.

b

а

с

здесь в качестве составных частей разложения фигурируют только треугольники.
АВС –

прямоугольный треугольник.
СD перпендикулярна EF,
C принадлежит EF,
PО и KN параллельны EF.

В данном разложении части квадратов, расположенных на катетах образуют квадрат на гипотенузе.

три прямоугольных треугольника составляют трапецию. Поэтому площадь этой фигуры можно

находить по формуле площади прямоугольной трапеции, либо

как сумму площадей трех треугольников. В первом случае S=½ (a + b)(a + b), во втором S=½ab + ½ab + ½c² приравнивая эти выражения получим:
½ (a² + 2ab + b²)= ab + ½ c²;
½ a² + ab + ½ b² = ab + ½ c²;
½ a² + ½ b² = ½ c²;
a² + b² = c².
Теорема доказана.

= 90, ВС = b,
АС

= а, АВ = с
Доказать: с² = а² + b²

Доказательство:
Достроим АВС до квадрата СМРК со стороной (а + b), тогда SСМРК =(а+b)²
С другой стороны площадь квадрата равна сумме площадей 4 равных

М

К

Р

Т

Н

прямоугольных , площадь каждого из которых равна ½аb, и площади квадрата со стороной равной с, поэтому
SСМРК = 4· ½аb + с². Таким образом (а + b)² =4· ½аb + с²,
а² + 2аb + b² = 2аb + c²,
а² + 2аb + b² – 2аb = c²,
а² + b² = c². Теорема доказана.

Евклидом в его "Началах". По свидетельству Прокла (Византия), оно придумано

самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал".

квадраты и доказывается, что прямоугольник BNLD равновелик квадрату BFHА, а

прямоугольник NCEL - квадрату АMКС. Тогда сумма площадей квадратов на катетах будет равна площади квадрата на гипотенузе.

SABD = ½ SBNLD = ½BD · LD;
SBFC= ½ SBFHA = ½BF · BA.
Значит прямоугольник BNLD равновелик квадрату BFHА.

В самом деле, треугольники ABD и BFC равны по двум сторонам и углу между ними: FB=AB; BC=BD; ∟АВD=∟FBC=∟ABC+90º

Аналогично доказывается, что SNCEL=SAMКС.
Итак, SABFH+SAMКС=SBNLD+SNCEL=SBCED. Теорема доказана.

можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а.

Таким образом d²= a² + a²=2a², d=a 2 .

Рассмотрим примеры практического применения теоремы Пифагора. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур.

2. Диагональ куба d является гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (d1 = a 2 ). Отсюда имеем:
d²=a²+2a², d²=3a², d=a 3

о важности теоремы. Значение ее состоит прежде всего в том,

что из нее или с ее помощью можно вывести большинство теорем геометрии.
Теорема и уравнение Пифагора на протяжении тысячелетий привлекают внимание математиков, являясь источником плодотворных идей и открытий.