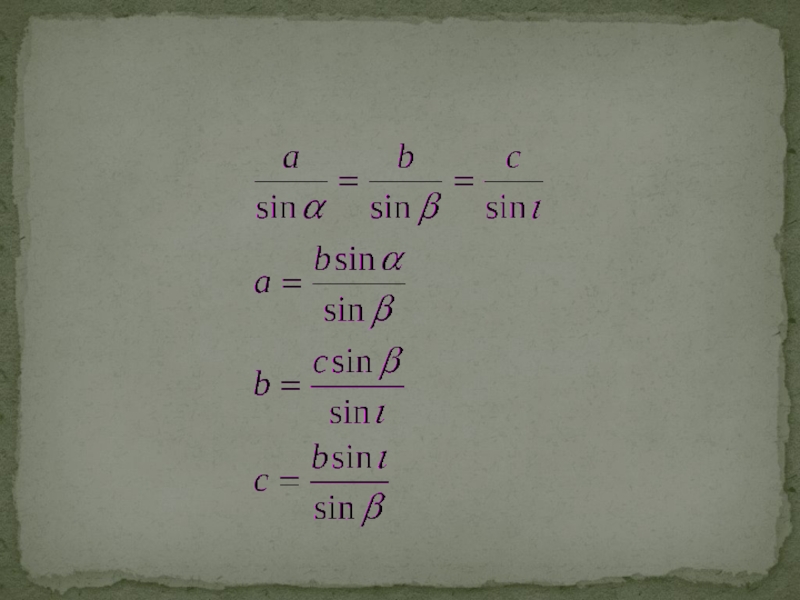Теорема синусов

Содержание

1. Теорема синусов
2. Теоре́ма си́нусов — теорема, устанавливающая зависимость между
3. Слайд 3
4. Для произвольного треугольника\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma}
5. Слайд 5
6. В n-мерном симплексе имеется соотношениеR_n=\frac{R_{n-1}^i}{\sin (2{\cdot} {A_{n-1}^i})},где
7. Слайд 7
8. Самое древнее доказательство для теоремы синусов на
9. Конец!
10. Скачать презентанцию

Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и противолежащими им углами. Существуют два варианта теоремы; обычная теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов

Слайды и текст этой презентации

Слайд 1Теорема Синусов

Слайд 2Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и

противолежащими им углами. Существуют два варианта теоремы; обычная теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов

Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и противолежащими им углами. Существуют два варианта теоремы;

Слайд 3

Слайд 4Для произвольного треугольника
\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2{\cdot}R,
где a,

b, c — стороны треугольника, \alpha, \beta, \gamma — соответственно

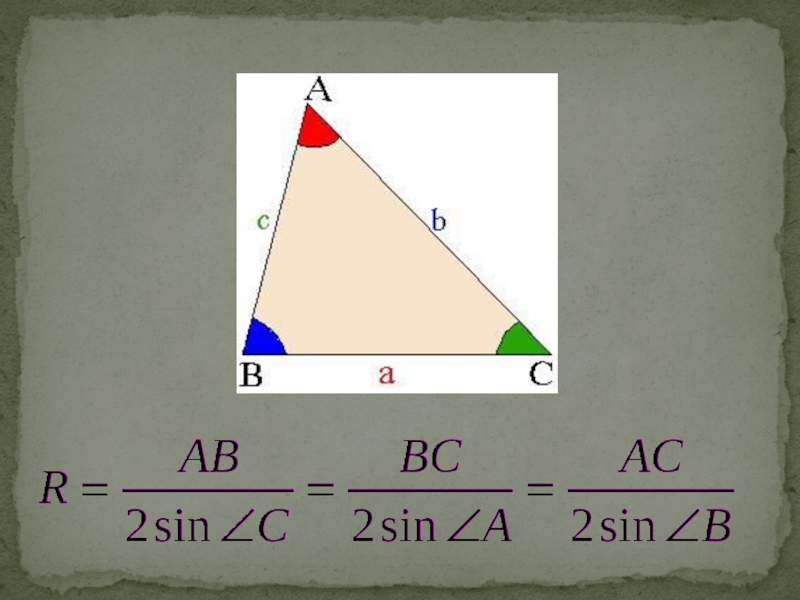
противолежащие им углы, а R — радиус окружности, описанной вокруг треугольника.

$Для произвольного треугольника\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2{\cdot}R,где a, b, c — стороны треугольника, \alpha, \beta,$

Слайд 5

Слайд 6В n-мерном симплексе имеется соотношение
R_n=\frac{R_{n-1}^i}{\sin (2{\cdot} {A_{n-1}^i})},
где R_n — радиус

описанной сферы; R_{n-1}^i — радиус описанной (n-1)-мерной сферы i-грани; A_{n-1}^i

— угловой радиус описанного конуса вокруг i-ой вершины.

Обобщение

$В n-мерном симплексе имеется соотношениеR_n=\frac{R_{n-1}^i}{\sin (2{\cdot} {A_{n-1}^i})},где R_n — радиус описанной сферы; R_{n-1}^i — радиус описанной (n-1)-мерной$

Слайд 7

Слайд 8Самое древнее доказательство для теоремы синусов на плоскости описано в

книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике» написанной в

XIII веке. Теорема синусов для сферического треугольника была доказана математиками средневекового Востока ещё в X векеВ труде Ал-Джайяни XI века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере.

История

Самое древнее доказательство для теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном

Слайд 9Конец!

Скачать презентацию

Разделы презентаций

Теорема синусов

Содержание

Слайды и текст этой презентации

Слайд 1Теорема Синусов

Слайд 2Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и

противолежащими им углами. Существуют два варианта теоремы; обычная теорема синусов.

Слайд 3

Слайд 4Для произвольного треугольника
\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2{\cdot}R,
где a,

b, c — стороны треугольника, \alpha, \beta, \gamma — соответственно

Слайд 5

Слайд 6В n-мерном симплексе имеется соотношение
R_n=\frac{R_{n-1}^i}{\sin (2{\cdot} {A_{n-1}^i})},
где R_n — радиус

описанной сферы; R_{n-1}^i — радиус описанной (n-1)-мерной сферы i-грани; A_{n-1}^i

Слайд 7

Слайд 8Самое древнее доказательство для теоремы синусов на плоскости описано в

книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике» написанной в

Слайд 9Конец!

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Теорема синусов

Содержание

Слайды и текст этой презентации

Слайд 1Теорема Синусов

Слайд 2Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и

противолежащими им углами. Существуют два варианта теоремы; обычная теорема синусов.

Слайд 3

Слайд 4Для произвольного треугольника\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2{\cdot}R,где a,

b, c — стороны треугольника, \alpha, \beta, \gamma — соответственно

Слайд 5

Слайд 6В n-мерном симплексе имеется соотношениеR_n=\frac{R_{n-1}^i}{\sin (2{\cdot} {A_{n-1}^i})},где R_n — радиус

описанной сферы; R_{n-1}^i — радиус описанной (n-1)-мерной сферы i-грани; A_{n-1}^i

Слайд 7

Слайд 8Самое древнее доказательство для теоремы синусов на плоскости описано в

книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике» написанной в

Слайд 9Конец!

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 4Для произвольного треугольника
\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2{\cdot}R,
где a,

Слайд 6В n-мерном симплексе имеется соотношение
R_n=\frac{R_{n-1}^i}{\sin (2{\cdot} {A_{n-1}^i})},
где R_n — радиус