Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрические уравнения (10 класс)
Содержание
- 1. Тригонометрические уравнения (10 класс)
- 2. КРОССВОРД
- 3. КРОССВОРД
- 4. КРОССВОРД
- 5. КРОССВОРД
- 6. КРОССВОРД
- 7. КРОССВОРД
- 8. ЧТОБЫ ПРАВИЛЬНО РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ НАДО:1) уметь
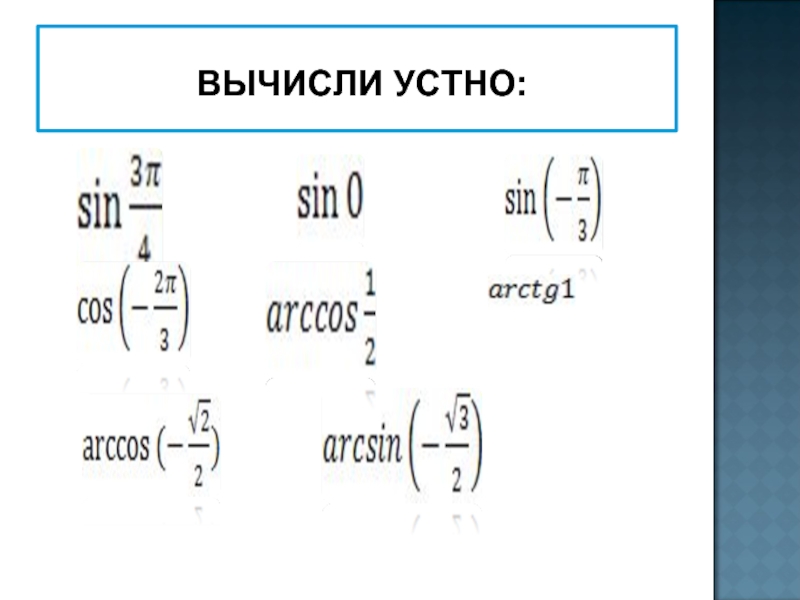
- 9. ВЫЧИСЛИ УСТНО:
- 10. ОТВЕТЫ:
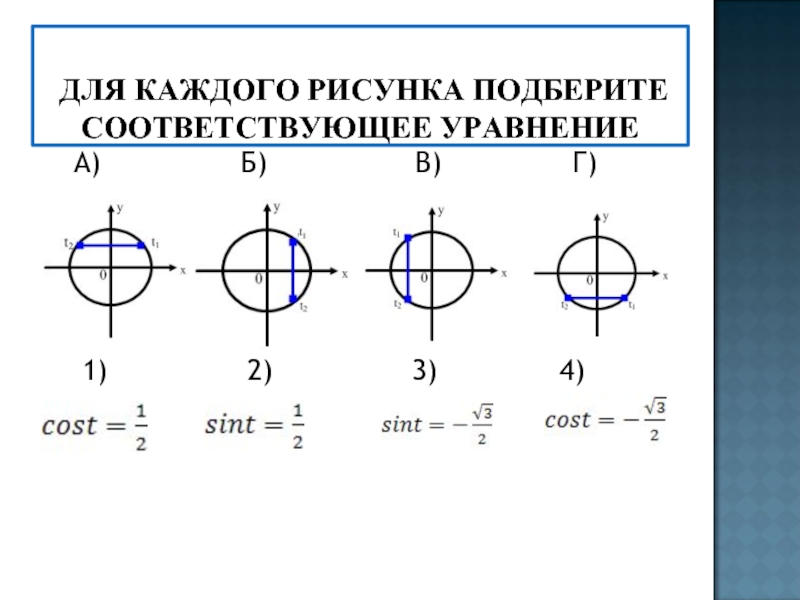
- 11. ДЛЯ КАЖДОГО РИСУНКА ПОДБЕРИТЕ СООТВЕТСТВУЮЩЕЕ УРАВНЕНИЕ
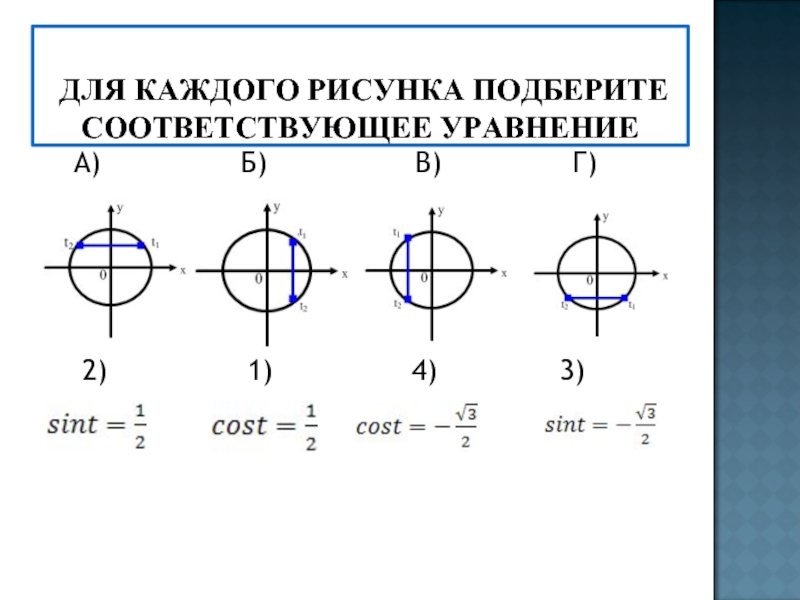
- 12. ДЛЯ КАЖДОГО РИСУНКА ПОДБЕРИТЕ СООТВЕТСТВУЮЩЕЕ УРАВНЕНИЕ
- 13. УСТАНОВИТЕ СООТВЕТСТВИЕ:1) sin x = 0
- 14. УСТАНОВИТЕ СООТВЕТСТВИЕ:1) sin x = 0
- 15. УСТАНОВИТЕ СООТВЕТСТВИЕ:1) sin x = 0
- 16. УСТАНОВИТЕ СООТВЕТСТВИЕ:1) sin x = 0
- 17. УСТАНОВИТЕ СООТВЕТСТВИЕ:1) sin x = 0
- 18. УСТАНОВИТЕ СООТВЕТСТВИЕ:1) sin x = 0
- 19. Решим при помощичисловой окружности уравнение sin t=a, IаI
- 20. sin t = а ,|a|< 1
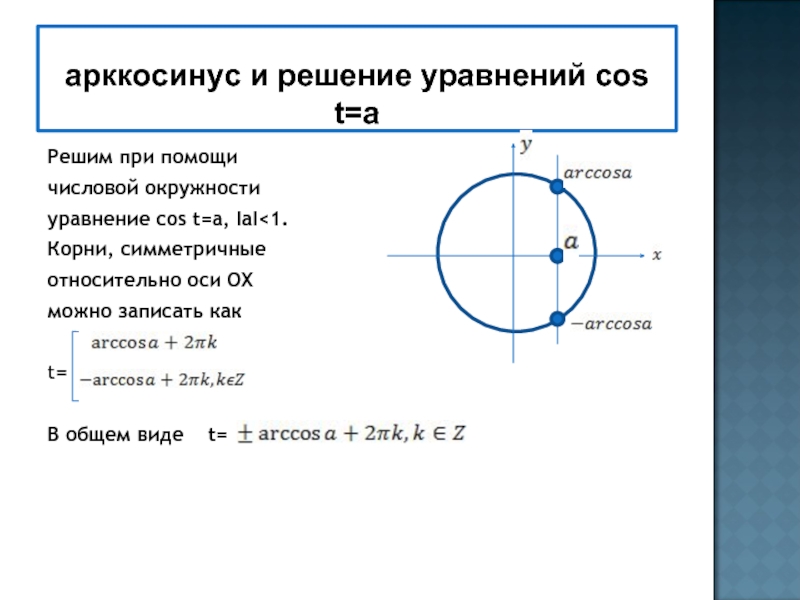
- 21. арккосинус и решение уравнений соs t=aРешим при
- 22. соs t =а , |a|< 1
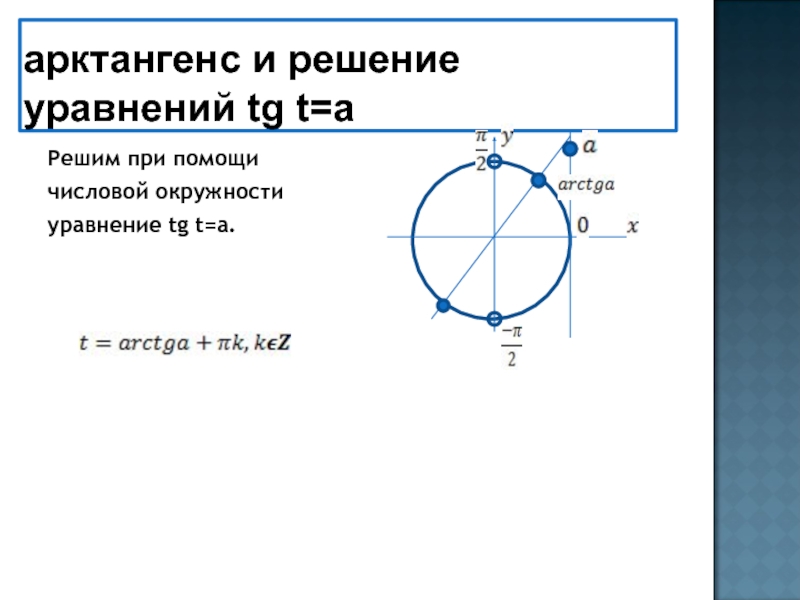
- 23. арктангенс и решение уравнений tg t=aРешим при помощичисловой окружностиуравнение tg t=a.
- 24. tg t = а Частные
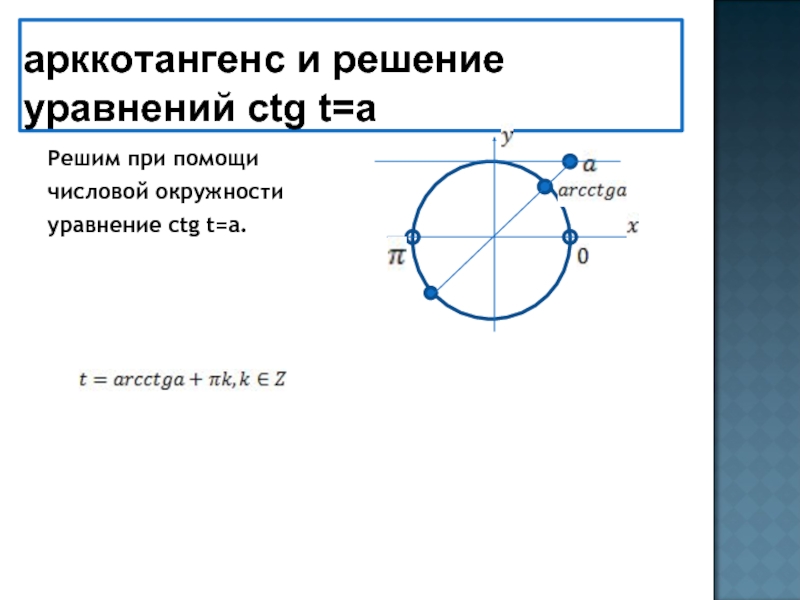
- 25. арккотангенс и решение уравнений ctg t=aРешим при помощичисловой окружностиуравнение ctg t=a.
- 26. сtg t = а,
- 27. Слайд 27
- 28. МЕТОДЫ РЕШЕНИЯ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ
- 29. НАША ЗАДАЧА: СВЕСТИ ЛЮБОЕ ТРИГОНОМЕТРИЧЕСКОЕ УРАВНЕНИЕ К ПРОСТЕЙШЕМУ ВИДУ.
- 30. ПРИМЕРЫ УРАВНЕНИЙх= ±arccos а + 2 k, k є Z
- 31. ПРИМЕРЫ УРАВНЕНИЙ х = (-1)n arcsin a+πn,n
- 32. ПРИМЕРЫ УРАВНЕНИЙЭто частный вид уравнения cos t=0, t=
- 33. ПРИМЕРЫ УРАВНЕНИЙx = arctg a + πk,k є z
- 34. РЕШИ САМ Уровень А Уровень БРешите
- 35. РЕШИ САМ Уровень А
- 36. ЗАДАЧА ПРАКТИЧЕСКОГО СОДЕРЖАНИЯИмеется функция
- 37. Скачать презентанцию
КРОССВОРД
Слайды и текст этой презентации
Слайд 1ПРОСТЕЙШИЕ ТРИГОНОМЕТРИ ЧЕСКИЕ УРАВНЕНИЯ
Учитель 1 квалификационной категории Алейникова Л.В.
МБОУ
«Гатчинская средняя общеобразовательная школа №1»
Слайд 8ЧТОБЫ ПРАВИЛЬНО РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ НАДО:
1) уметь отмечать точки на
числовой окружности;
2) уметь определять значения синуса, косинуса, тангенса и котангенса
для координат точек числовой окружности;3) знать свойства основных тригонометрических функций;
4) знать понятие арксинуса, арккосинуса, арктангенса, арккотангенса и уметь отмечать их на числовой окружности.
Слайд 13УСТАНОВИТЕ СООТВЕТСТВИЕ:
1) sin x = 0
а)
2) cos x = -1
б) 3) sin x = 1 в)
4) tg x = 1 г)
5) ctgx = 0 д)
Слайд 14УСТАНОВИТЕ СООТВЕТСТВИЕ:
1) sin x = 0
а)
2) cos x = -1
б) 3) sin x = 1 в)
4) tg x = 1 г)
5) ctgx = 0 д)
Слайд 15УСТАНОВИТЕ СООТВЕТСТВИЕ:
1) sin x = 0
а)
2) cos x = -1
б) 3) sin x = 1 в)
4) tg x = 1 г)
5) ctgx = 0 д)
Слайд 16УСТАНОВИТЕ СООТВЕТСТВИЕ:
1) sin x = 0
а)
2) cos x = -1
б) 3) sin x = 1 в)
4) tg x = 1 г)
5) ctgx = 0 д)
Слайд 17УСТАНОВИТЕ СООТВЕТСТВИЕ:
1) sin x = 0
а)
2) cos x = -1
б) 3) sin x = 1 в)
4) tg x = 1 г)
5) ctgx = 0 д)
Слайд 18УСТАНОВИТЕ СООТВЕТСТВИЕ:
1) sin x = 0
а)
2) cos x = -1
б) 3) sin x = 1 в)
4) tg x = 1 г)
5) ctgx = 0 д)
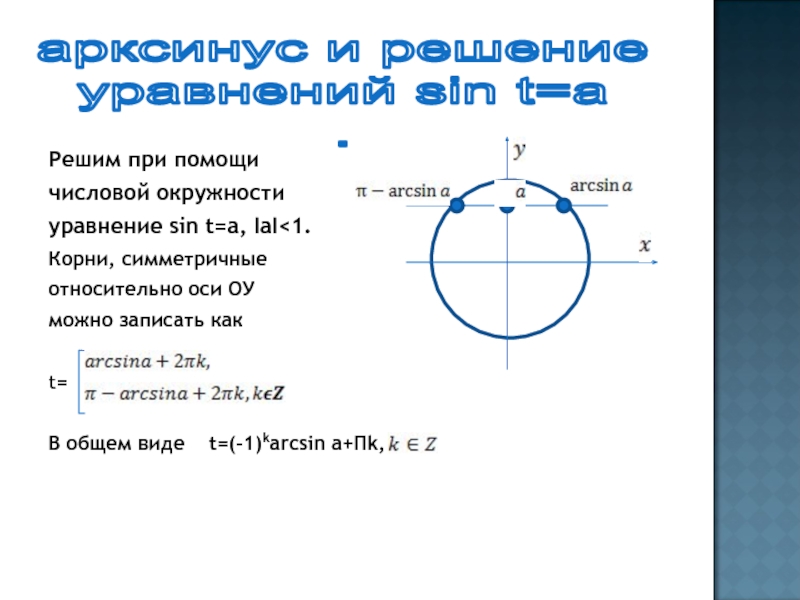
Слайд 19Решим при помощи
числовой окружности
уравнение
sin t=a, IаI
общем виде t=(-1)karcsin a+Пk,арксинус и решение
уравнений sin t=a
.
Слайд 20sin t = а ,|a|< 1
Частные случаи:
а
= 0
а = -1 а = 1t = π k, t = π/2+ 2 π k, t = π/2 + 2πk, kєZ k є Z kє Z
аrcsin (-а) = - аrcsin а
t π /6 π /4 π /3
sint 1/2 √2 / 2 √3 / 2
Слайд 21арккосинус и решение уравнений соs t=a
Решим при помощи
числовой окружности
уравнение cos t=a, IаI
оси ОXможно записать как
t=
В общем виде t=
Слайд 22соs t =а , |a|< 1
Частные случаи:
а =
0
а = -1 а = 1t= π/2 + π k, t= π + 2 π k, t= 2 π k,
k є Z k є Z k є Z
аrcсos (-а) = π - аrcсos а
t π /6 π /4 π /3
cost √3 / 2 √2 /2 1/2
Слайд 24tg t = а
Частные случаи:
а = 0
а
= -1 а = 1t = πk, k є Z t = -π/4 + π k t = π/4 + π k
аrctg (-а) = - аrctg а
t π /6 π /4 π /3
tg t √3 / 3 1 √3
Слайд 25арккотангенс и решение уравнений ctg t=a
Решим при помощи
числовой окружности
уравнение ctg
t=a.
Слайд 26сtg t = а,
Частные случаи:
а = 0
а = -1 а = 1
t = π/2 + π k, t = 3π/4+ πk, t= π/4+ πk ,
k є Z k є Z k є Z
аrcсtg (-а) = π - аrcсtg а
t π /6 π /4 π /3
ctgt √3 1 √3 / 3
Слайд 28
МЕТОДЫ РЕШЕНИЯ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ
УРАВНЕНИЙ
ghb
Применение
формул корней
Метод введения новой переменной
V
Метод
разложения
на множители
Слайд 36ЗАДАЧА ПРАКТИЧЕСКОГО СОДЕРЖАНИЯ
Имеется функция
,
где I – сила переменного тока . Определить такие моменты времени t, когда сила тока I равна 2 амперам.
Теги