Тригонометрия в жизни

математические понятия, связанные с ней
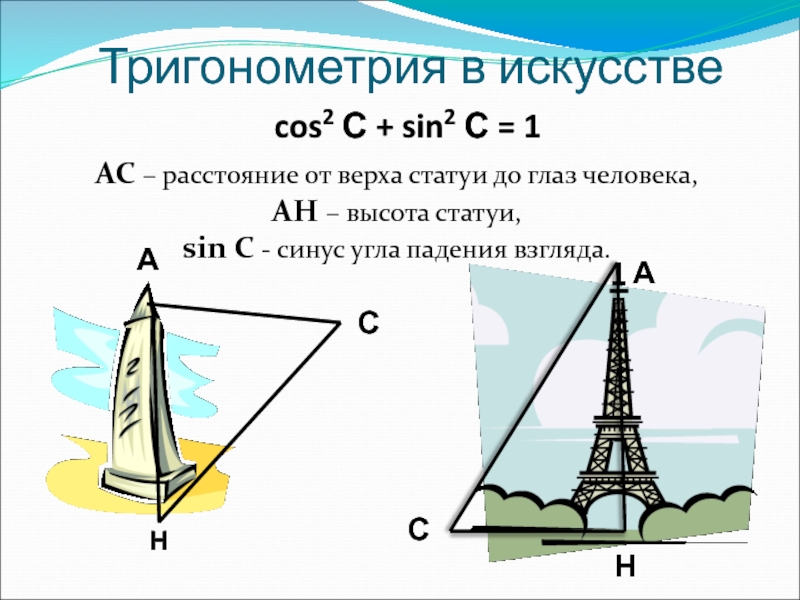
Узнать, в каких сферах науки и

искусства применяется тригонометрия
научиться использовать знания, полученные на уроках алгебры, в задачах с практическим содержанием
создать условия для поддержания интереса к математике через использование обобщающих приёмов умственной деятельности;
способствовать самостоятельной деятельности учащихся;
развивать логическое мышление.
 научиться решать тригонометрические задачи с целью лучшей подготовки к ЕГЭ

в
море.

Древние люди вычисляли
высоту дерева,
сравнивая длину его тени

с
длиной тени от шеста,
высота которого была известна.

до н.э.)
Таблица числовых значений хорд
Таблица для определения соотношений

между элементами треугольников

Первая таблица синусов, высчитанная по хордам в окружности
«Альмагест – самая значимая тригонометрическая работа всей античности

Клавдий Птолемей (90 – 168 г н.э)

синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов
Установил

основные соотношения между этими линиями
Дал определения функциям
Установил формулу двойного угла

Ал-Батани
( ок. 900 г. н.э)

Абу-ль-Вефа
( 940 – 997 г. н.э)

Дополнил и систематизировал различные случаи решения плоских и сферических треугольников

Открыл «плоскую» теорему косинусов и формулы тригонометрических функций от кратных углов

Разложил функции в ряды и открыл путь для их использования в математическом анализе

и принятую в наши дни символику
Разъяснил вопрос о знаках

всех тригонометрических функций любого аргумента

Ричард Саусвелл (1888-1970)

Разработал метод проектирования сложных форм в 1920 году;

Выразил тригонометрические функции как отношение координат x, y, z к длине элемента.

– расстояние от верха статуи до глаз человека,
АН – высота

статуи,
sin С - синус угла падения взгляда.

А

С

Н

А

С

Н

закону косинуса или синуса (гармоническому закону), называются гармоническими колебаниями.

Выражение, стоящее

под знаком косинуса или синуса, называется фазой колебания:

косинусом.

или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть

траекторию движения.

При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.

свет испытывает преломление в капельках воды, взвешенных в воздухе по

закону преломления:


n1 - показатель преломления первой среды  n2 - показатель преломления второй среды
α-угол падения, β-угол преломления света

sin α / sin β = n1 / n2

Най­ди­те