Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол между прямой и плоскостью (10 класс)
Содержание
- 1. Угол между прямой и плоскостью (10 класс)
- 2. Перпендикулярны ли прямые а и в? Ответ обоснуйте.АВСDFbaABCD- прямоугольник, FB┴(ABC)ABCD- параллелограмм, FB┴(ABC)
- 3. Перпендикулярны ли прямые а и в? Ответ обоснуйте.АDCBOFbaABCD- прямоугольник, FB┴(ABC)ABCD- ромб, FB┴(ABC)a
- 4. Перпендикулярны ли прямые а и в? Ответ обоснуйте.BACDabBD┴ (ABC),∟ABC=40˚,∟BAC=50˚ACBDbaBD┴ (ABC),∟ABC=10˚,∟BAC=70˚
- 5. Угол между прямой и плоскостьюГеометрия полна приключений,
- 6. Должны узнать- Что называется углом между прямой
- 7. Дороги не те знания, которые отлагаются в
- 8. АА1Как называется основание перпендикуляра, опущенного из т.А
- 9. aaЧто является проекцией прямой а на плоскость α? αα
- 10. Докажем, что проекцией прямой а на плоскостьα,
- 11. Изображения плоских фигур на стереометрических чертежах.Прямоугольник Прямоугольный треугольникРавносторонний треугольник
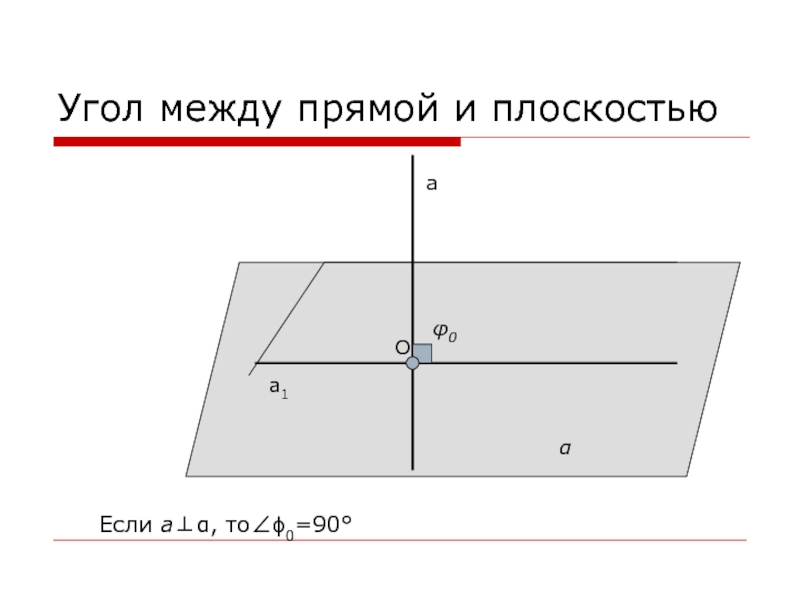
- 12. Угол между прямой и плоскостьюаа1αφ0сφHMOОпределение. Угол между
- 13. Угол между прямой и плоскостьюаа1αφ0OЕсли а⊥α, то∠ϕ0=90°
- 14. Угол между прямой и плоскостьюаαЕсли а⎪⎪α, то ∠ϕ0=0°
- 15. Рано или поздно всякая правильная математическая идея
- 16. Помните!Недостаточно лишь понять задачу, необходимо желание решить
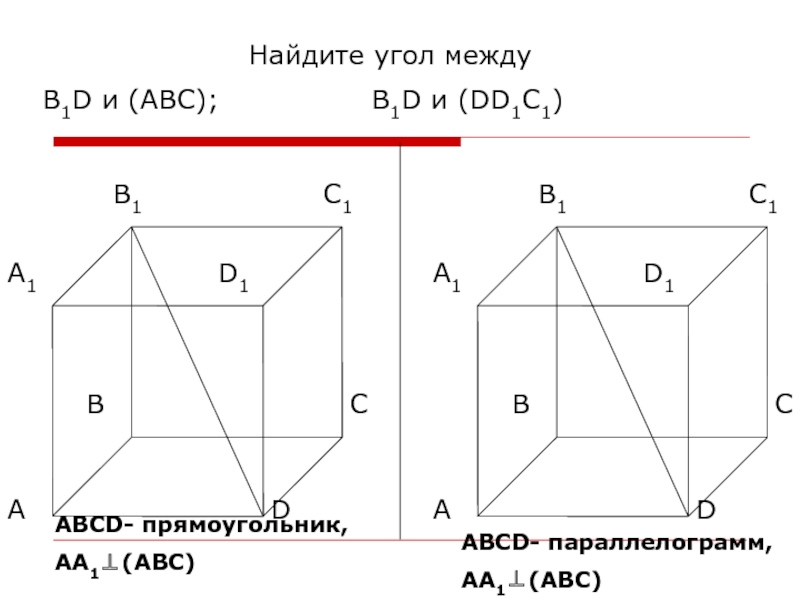
- 17. Найдите угол между В1D и (ABC); В1D и (DD1C1)АВСD- прямоугольник, АА1⊥(АВС) АВСD- параллелограмм, АА1⊥(АВС)
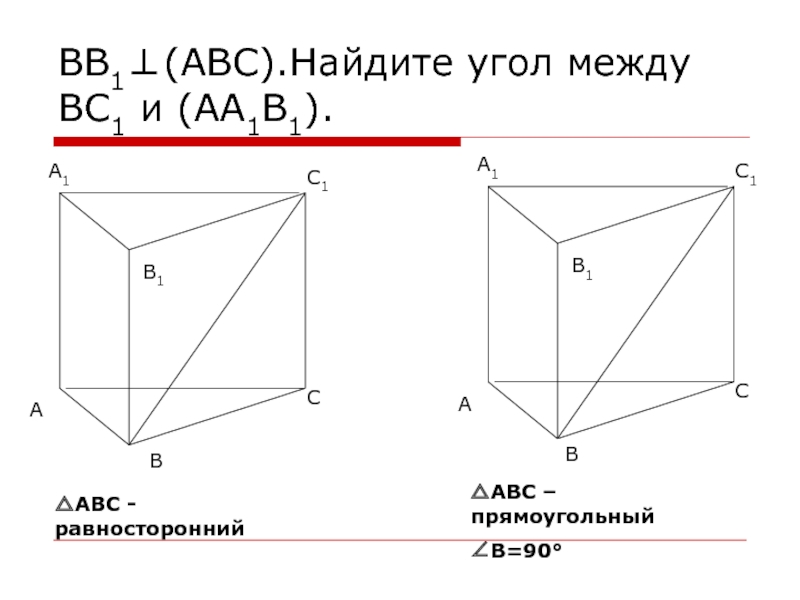
- 18. ВВ1⊥(АВС).Найдите угол между ВС1 и (АА1В1). △АВС - равносторонний△АВС – прямоугольный∠В=90°
- 19. ВВ1⊥(АВС).Найдите угол между ВС1 и (АА1В1). △АВС – тупоугольный, ∠В>90°
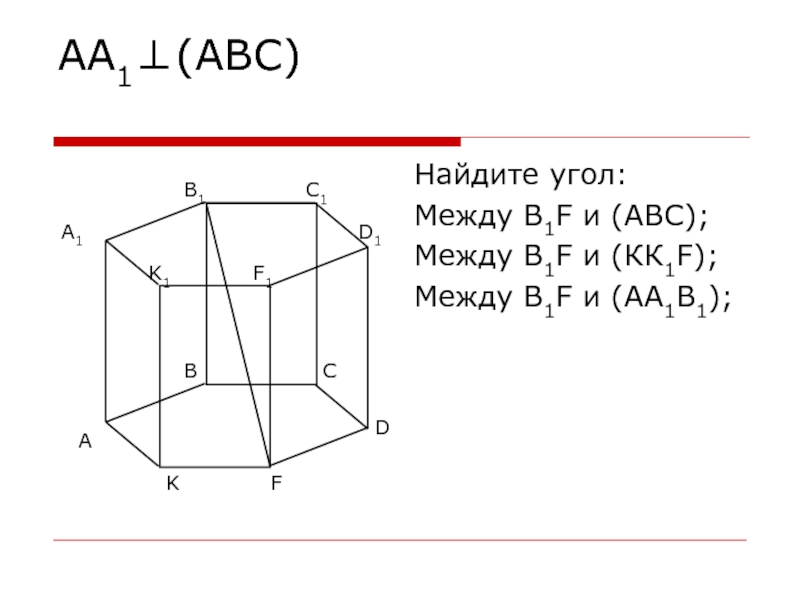
- 20. АА1⊥(АВС) Найдите угол:Между В1F и (АВС);Между В1F и (КК1F);Между В1F и (АА1В1);
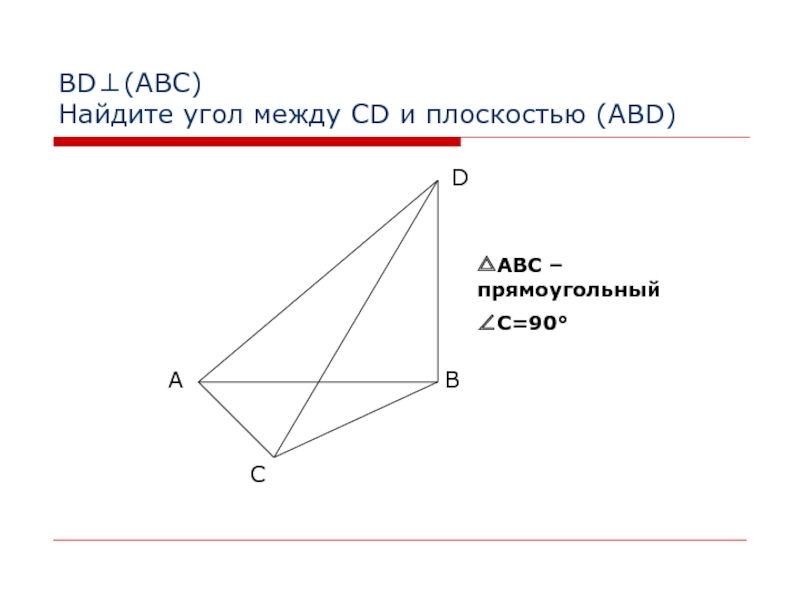
- 21. BD⊥(АВС) Найдите угол между CD и плоскостью (ABD)△АВС – прямоугольный∠C=90°
- 22. BD⊥(АВС) Найдите угол между CD и плоскостью (ABD)△АВС – равносторонний
- 23. BD⊥(АВС) Найдите угол между CD и плоскостью (ABD)△АВС – прямоугольный∠А=90°
- 24. Д/З № 164№149№158*Конспект.
- 25. Скачать презентанцию
Перпендикулярны ли прямые а и в? Ответ обоснуйте.АВСDFbaABCD- прямоугольник, FB┴(ABC)ABCD- параллелограмм, FB┴(ABC)
Слайды и текст этой презентации
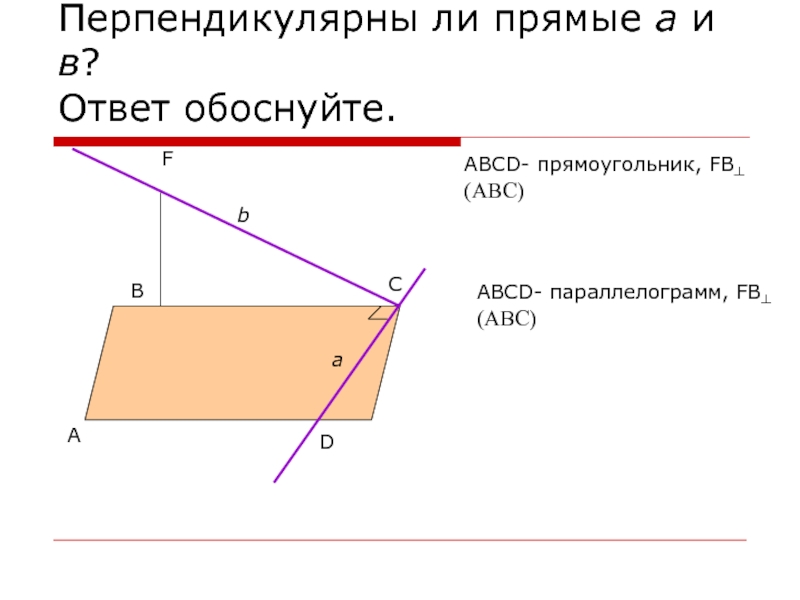
Слайд 2Перпендикулярны ли прямые а и в?
Ответ обоснуйте.
А
В
С
D
F
b
a
ABCD- прямоугольник, FB┴(ABC)
ABCD- параллелограмм,
FB┴(ABC)
Слайд 3Перпендикулярны ли прямые а и в?
Ответ обоснуйте.
А
D
C
B
O
F
b
a
ABCD- прямоугольник, FB┴(ABC)
ABCD- ромб,
FB┴(ABC)
a
Слайд 4Перпендикулярны ли прямые а и в?
Ответ обоснуйте.
B
A
C
D
a
b
BD┴ (ABC),
∟ABC=40˚,
∟BAC=50˚
A
C
B
D
b
a
BD┴ (ABC),
∟ABC=10˚,
∟BAC=70˚
Слайд 5Угол между прямой и плоскостью
Геометрия полна приключений, потому, что за
каждой задачей скрывается приключение мысли. Решить задачу – это значит
пережить приключение.В. Произволов.
Слайд 6Должны узнать
- Что называется углом между прямой и плоскостью?
- Как
построить угол между прямой и плоскостью?
- В каких задачах может
потребоваться угол между прямой и плоскостью?- Как обозначить этот угол ?
Слайд 7Дороги не те знания, которые отлагаются в мозгу, как жир,
дороги те, которые превращаются в умственные мышцы.
Герберт Спенсер (1820-1903) английский
философ и социолог
Слайд 8
А
А1
Как называется основание перпендикуляра, опущенного из т.А на плоскость α?
Ортогональная проекция
При изучении стереометрии важное значение
имеет изображение пространственных
фигур на чертеже. Фигура F1 –проекция фигуры F ,если она состоит из всех проекций точек фигуры F.
F
F1
Слайд 10Докажем, что проекцией прямой а на плоскостьα, не перпендикулярную этой
прямой, является прямая.
а
α
О
М
Н
β
а1
М1
Н1
МН⎪⎪М1Н1
МН⊥α
⇒
⇒
М1Н1⊥α ( по свойству параллельных прямых)
тН –
проекция т МтН1-проекция т М1
а1- проекция а
■
⇒
Слайд 11Изображения плоских фигур на стереометрических чертежах.
Прямоугольник
Прямоугольный треугольник
Равносторонний треугольник
Слайд 12
Угол между прямой и плоскостью
а
а1
α
φ0
с
φ
H
M
O
Определение. Угол между прямой и плоскостью,
пересекающей эту прямую и не перпендикулярно к ней, называется угол
между прямой и её проекцией на эту плоскость.∠ϕ0<∠ϕ
Слайд 15Рано или поздно всякая правильная математическая идея находит применение в
том или ином деле. Алексей Николаевич Крылов (1863-1945) Советский кораблестроитель, механик
и математик, академикС каким новым понятием познакомились?
Угол между прямой и плоскостью
Что называется углом между прямой и плоскостью?
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярно к ней, называется угол между прямой и её проекцией на эту плоскость.
Как построить угол между прямой а и плоскостью α?
а
α
О
М
Н
а1
План
Выбрать т. М на прямой а
Опустить МН⊥α
Построить ОН=а1- проекция прямой а
∠ϕ=∠(а, α)- искомый.
ϕ
Слайд 16Помните!
Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного
желания решить трудную задачу невозможно, но при наличии такового –
возможно. Где есть желание, найдется путь!Пойя. Д.
Слайд 17Найдите угол между
В1D и (ABC); В1D и (DD1C1)
АВСD-
прямоугольник,
АА1⊥(АВС)
АВСD- параллелограмм,
АА1⊥(АВС)
Теги
