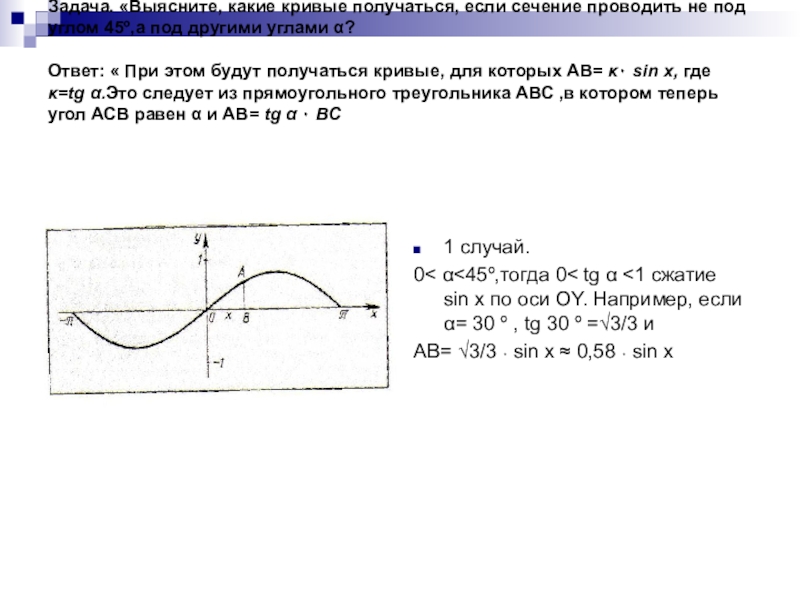
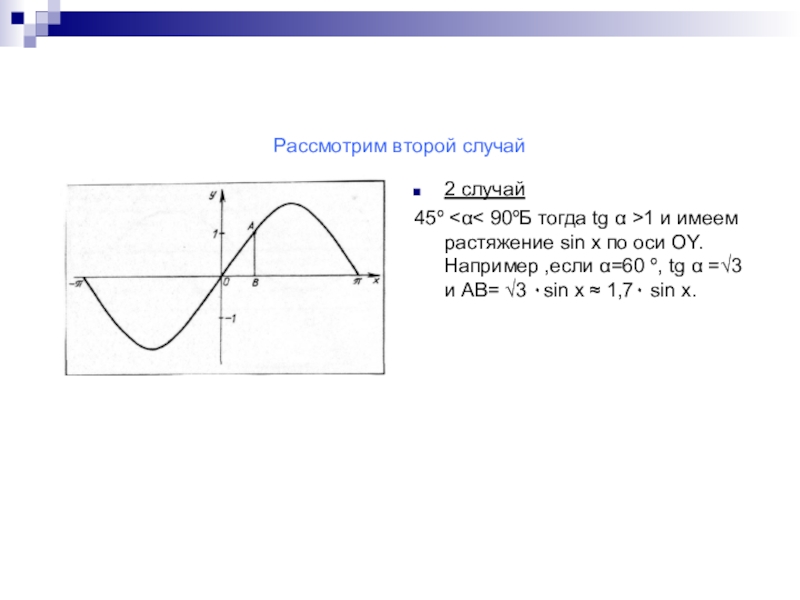
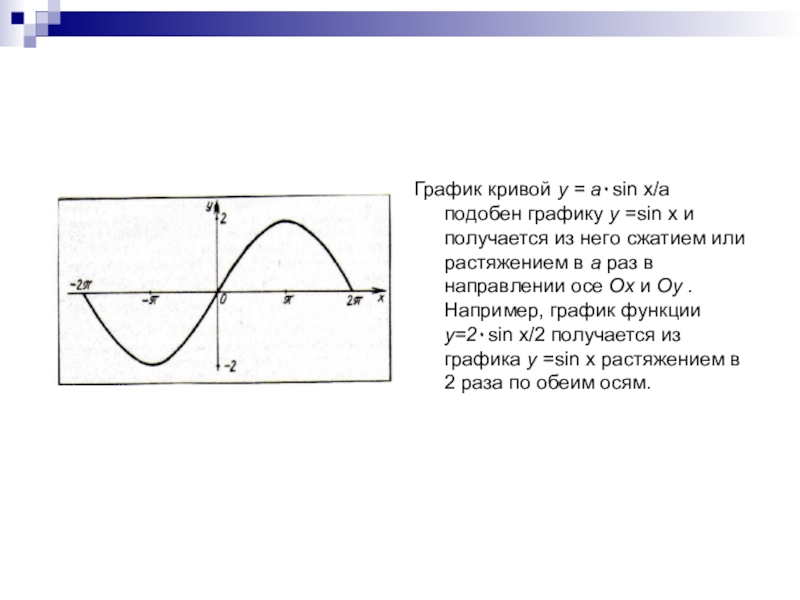
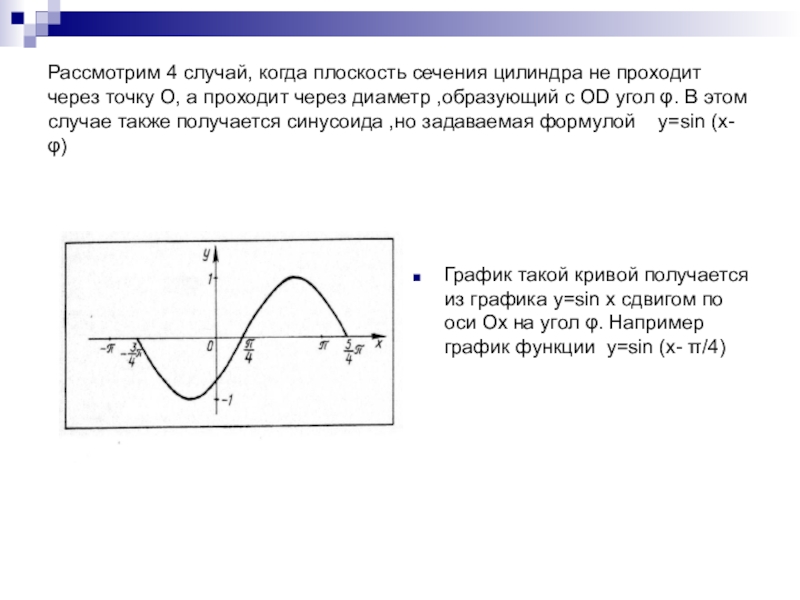
в построении графика функции у=sinx.
Рассмотреть вопрос о преобразовании графиков(
сжатие и растяжение вдоль осей Ох и Оу)Через решение практической задачи показать связь между математикой и физикой.