Слайд 1Использование элементов технологии самосовершенствования личности на уроках математики
в классах
коррекционно – компенсирующего обучения
Работа
учителя математики
МОУ специальной (коррекционной)
школы-интерната №9
для детей-сирот и детей,
оставшихся без попечения родителей
Новиковой Екатерины Николаевны
Слайд 2
По данным НИИ детства, ежегодно рождается 5 - 8℅
детей с наследственной патологией,
8 – 10 % имеют выраженную
врождённую или приобретенную патологию,
4 – 5% составляют дети – инвалиды, значительное число
детей имеют стертые
нарушения развития.
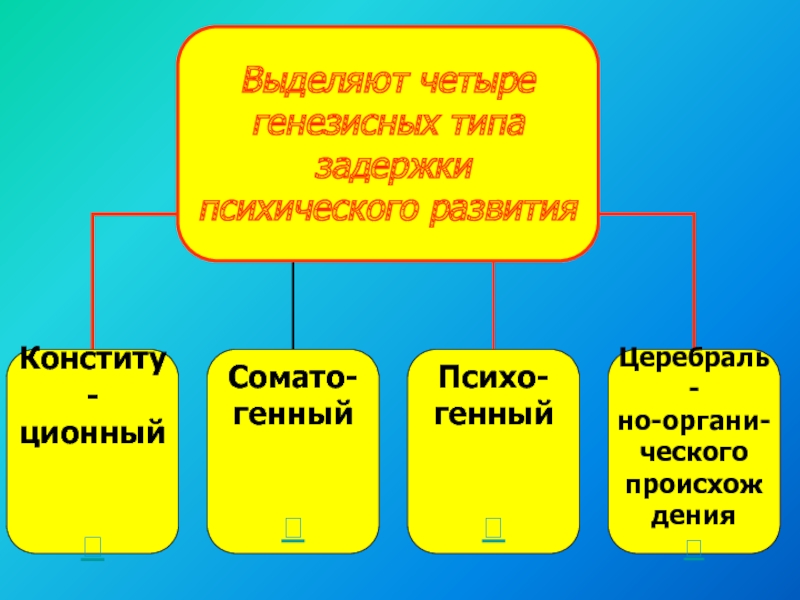
Слайд 4 ЗПР
конституционального происхождения
Состояние ЗПР определяется наследственностью.
Дети отличаются гармоничной
незрелостью одновременно телосложения и психики, поэтому такую форму задержки
обозначают, как гармонический психофизический инфантилизм.
Слайд 5 ЗПР
соматогенного происхождения
Дети рождаются
у здоровых родителей.
ЗПР- следствие перенесенных в раннем детстве заболеваний,
влияющих на развитие мозговых функций:
✶ хронических инфекций,
✶ аллергии,
✶ дистрофии,
✶ дизентерии.
Длительные, тяжело протекающие, часто хронические заболевания резко снижают психический тонус детей.
Слайд 6ЗПР
психогенного происхождения
Дети имеют нормальное физическое развитие, соматически здоровы.
По данным исследований,
у большинства имеется
мозговая дисфункция.
Очаг формирования
данной детской аномалии - неблагополучные семьи.
Слайд 7 ЗПР
церебрально-органического происхождения
ЗПР обусловлено более стойким локальным нарушением
созревания мозговых структур.
Причины отклонений в развитии мозга:
патология беременности;
алкоголизм, наркомания матери или отца;
родовые патологии:
✓недоношенность;
✓родовая травма;
✓асфиксия (удушье плода);
тяжелые заболевания на первом году жизни;
тяжелые инфекционные заболевания.
Слайд 8 • На уроках математики, как и на других уроках,
необходимо создавать оптимальные условия для усвоения программного материала.
• Важное
внимание должно быть уделено отбору базового материала, который осуществляется в соответствии с принципом доступности.
Слайд 9 • Учебный материал по содержанию и объему должен быть
посильным для учащихся.
• Процесс обучения необходимо сделать проще и
легче путем детального объяснения и с систематическим повтором, многократной тренировкой в применении знаний.
Слайд 10 обеспечивать возможность ученику работать в свойственном ему темпе деятельности
контролировать
усвоение каждой части
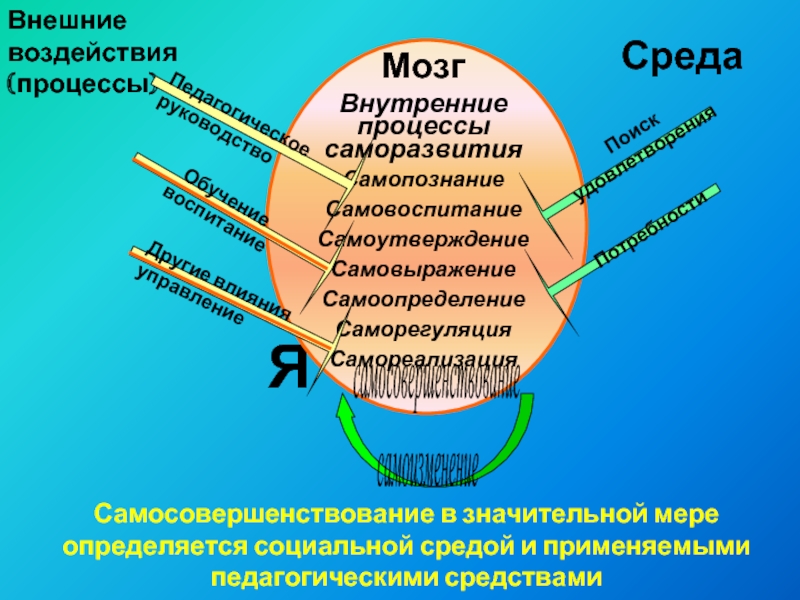
Слайд 11Я
Внешние воздействия (процессы)
самосовершенствование
самоизменение
Среда
Самосовершенствование в значительной
мере определяется социальной средой и применяемыми педагогическими средствами
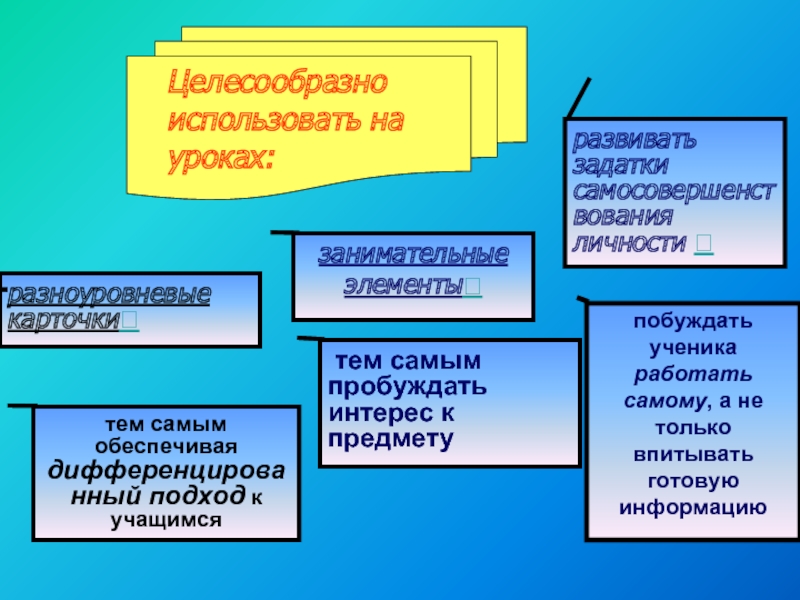
Слайд 12занимательные элементы
разноуровневые карточки
развивать задатки самосовершенствования личности
тем самым обеспечивая
дифференцированный подход к учащимся
тем самым пробуждать интерес к
предмету
побуждать ученика работать самому, а не только впитывать готовую информацию
Слайд 13 Тема: «Координатная плоскость»
Карточка №2
«Отметьте на координатной плоскости точки,
заданные координатами, соедините их отрезками в порядке следования.
Изображение какого
животного получилось?»
A (-4; 4); В (-3; 4); С (-3; 3); D (-1; 2); E (4; 1); G (7; 0); L (4; 0); К (4; -4); M (3; -4); N (3; -2); P (-1; -1); S (-1;-1); T (-1; -4);
R (-2; -4); H (-2; -1); Q (-4; 1); U (-6; 1); X (-6; 2); Y (-5; 2); 7 (-4; 3)
Слайд 14 Дети любят самостоятельные и исследовательские работы в форме игры
«Дешифровщик» -
выполнив математическое задание, дети составляют название,
например, какого-то исторического факта, о котором рассказал учитель.
Задания такого типа позволяют реализовывать межпредметные связи и развивают общую эрудицию учащихся.
Слайд 15Тема: «Сложение и вычитание десятичных дробей»
Как называется одно из государств
полуострова Индокитай? ( Лаос)
1) 27,5+х=41,83
К –69,33
Л –14,33 Р –14,78 С –13,78
2) Х-0,07=1,5
А –1,57 И –1,12 О –1,43 У –2,2
3) Х+17,51=21,12
М – 38,63 П – 2,61 Т – 4,39 О – 3,61
4) 8,127-х=5,548
Н – 13,675 С – 2,579 Р – 3,421 В – 3,579
Слайд 16 Задание на корректировку восприятия
Найти и исправить ошибки, если они
есть в следующих действиях:
а)3,2 4 + 8 = 4,0;
б) 29
+ 7,1 = 100;
в)16,6 - 5 = 16,1;
г) 25,16 + 0,4 =25,56.
Слайд 17Можно использовать задания ,решение которых будет соответствовать определенному цвету картинки
Слайд 18 Задание на анализ отношений
Слова из данного ниже списка расставьте в
окошки схемы на
Треугольник, четырехугольник, пятиугольник, шестиугольник,
прямоугольник, квадрат, многоугольник.
Слайд 19 Задание на классификацию
Даны три ряда чисел. Укажите, по
какому правилу составлен каждый ряд чисел, и продолжите его еще
на три числа в соответствии с этим правилом.
а)1, 3, 5, 7, 9, 11,....
б)2, 4, 6, 8, 10…
в) 1, 2, 4, 5, 7, 8, 10, 11, 13….
Слайд 20Упражнения для усвоения учащимися 5-6 классов приемов составления задач
1. Составьте
задачу, обратную следующей:
«На одной ферме 847 коров, а на другой—на
309 коров больше. Сколько коров на двух фермах?»
2. Составьте задачу по краткой записи:
— Зт
— на 1 т больше, чем
— в 2 раза меньше, чем —
3. Составьте задачи по выражениям:
a) 12∙64
b) 18∙79-12∙64
c)(18 ∙79 – 12∙64): 3
Слайд 214. «Купили 3 кг картофеля, 3 кг свеклы, 4 кг моркови,
5 кг яблок, 6 кг капусты,2 кг груш и 4
кг слив. Сколько было куплено килограммов овощей и сколько килограммов фруктов?» Составьте задачу, решаемую тем же способом, но с другим сюжетом.
5. Составьте задачи, при решении которых:
a). по известным частям находят целое;
b). по целому и его частям находят другую часть.
6. Составьте задачи, используя слова:
a) «ехали, проехали, осталось»;
b) «было, изменили, стало»;
c) «дороже» — «дешевле»;
d) «легче» — «тяжелее».
Слайд 22При изучении отдельных тем возможно применение эвристического метода обучения.
Учащимся
не сообщают готовых, подлежащих самостоятельному «открытию» правил - сохраняется видимость
игры, что позволяет поддерживать у ребенка иллюзию собственного открытия истины.
Слайд 23 Любое открытие, пусть самое маленькое, сделанное при решении
даже самой простой задачи, сродни большому открытию ученого.
Тем самым у ребенка пробуждается желание совершать новые открытия, самостоятельно добиваться каких–то успехов.
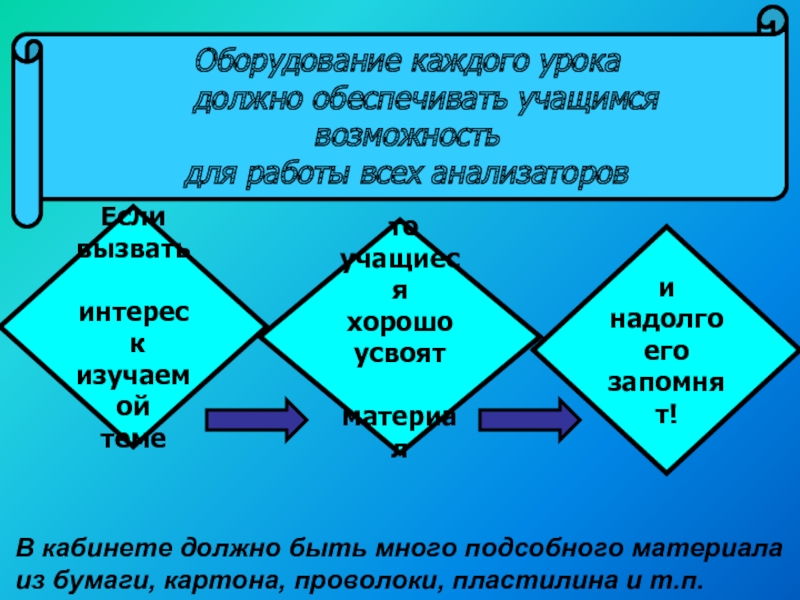
Слайд 24Оборудование каждого урока
должно обеспечивать учащимся
возможность
для работы всех
анализаторов
Если
вызвать
интерес
к изучаемой
теме
то учащиеся
хорошо
усвоят
материал
и надолго
его запомнят!
В кабинете должно быть много подсобного материала
из бумаги, картона, проволоки, пластилина и т.п.
Слайд 25Учащиеся охотно выполняют задания на компьютере
Например:
Отметить числа на координатной прямой
•
Отметить точки по заданным координатам
Определить координаты точек, задающих рисунок
Сравнить числа
Выполнить действия
Найти числа, противоположные данным
Слайд 26Блицопрос
Фронтальный опрос
Опрос-«вертушку» с консультантами
Работу парами или
в группе
Самостоятельную работу
Тестирование
Контроль и оценка
знаний —
важнейший
момент в организации
учебного процесса
Слайд 27Чтобы удержать внимание учащихся в течение всего урока, общую оценку
целесообразно выставлять в конце урока.
В течение урока каждый ученик
получает три-четыре отметки,
оценку «2» практически не получает никто из учащихся.
Оценивая ученика важно помнить, что отметка используется правильно лишь в том случае, когда она способствует достижению успеха и в целом развитию учащихся.
Слайд 28 Способы облегчения
трудных заданий:
дополнительные наводящие вопросы;
опорные, обобщающие схемы,
«программированные карточки»,
графические модели,
карточки-помощницы
приемы-предписания с указанием последовательности операций,
;
помощь в выполнении определенных операций;
образцы решения задач;
поэтапная проверка задач, упражнений.
Слайд 29Необходимо требовать от учащихся самостоятельное почтение и осмысление задания к
упражнению (не только при решении задач, но и при выполнении
различных видов примеров).
Ребенок дожжен стараться сам разобраться и понять задание, и обращаться к учителю лишь за помощью, а не за конкретным ответом на вопрос «Что надо делать?».
Слайд 30 Учить проверять
качество своей работы
(как по ходу ее выполнения так
и по конечному результату)
Развивать потребность детей в самоконтроле
(формировать осознанное отношение
к выполняемой работе)
Работая с детьми с ЗПР
учителю нужно
Для этого
на уроках
следует отводить
специальное время
на самопроверку
и взаимопроверку
выполненного
задания
Слайд 32Микроалгоритмическая
организация деятельности
учащихся на уроке
(выслушать устное задание
еще
раз)
Дополнительный
контроль за занятостью
ребенка ( при признаках
усталости смена
деятельности
на другую, более легкую)
Использование
разнообразных видов
занятий,
игровых моментов
Применение красочного
наглядного
дидактического материала
Организация
самопланирования и
самопроверки,
оречевление учеником
своей деятельности
Слайд 33Заботиться
о создании
общей
положительной
атмосферы
на уроке
Шире
опираться на
игру
как ведущую
деятельность
ребенка с ЗПР
Избегать
ощущения скуки
монотонности
посредством
включения
разных видов
деятельности
Снижать
тревожность детей,
исключая упреки,
выговор,
насмешку,
угрозы и т. д
Слайд 34.Нестандартные виды домашних заданий, как элемент технологии саморазвития личности
.
Определяющие требования к домашним заданиям:
- аккуратность,
-самостоятельность их выполнения.
. Знания могут быть глубокими, полными и прочными только в том случае, если они самостоятельно продуманы, усвоены путем преодоления некоторых трудностей.
Самостоятельный поиск решения воспитывает у учащихся
- убежденность в знаниях, уверенность в своих силах,
- формирует потребность самостоятельно заниматься учебной
деятельностью,
- воспитывает навыки самообразования.
В процессе самостоятельной домашней работы каждый школьник осуществляет самоконтроль, что предполагает развитие умений анализировать свои знания, находить недочеты и ошибки и затем исправлять их.
Слайд 35Индивидуальное домашнее задание
(карточка)