Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы (8 класс)
Содержание
- 1. Векторы (8 класс)
- 2. Историческая справкаТермин вектор (от лат. Vector –
- 3. Что такое вектор?
- 4. Геометрическое понятие вектораНаиболее наглядно величину и направление
- 5. Нулевой векторЛюбую точку плоскости можно считать вектором.
- 6. Длина вектораРасстояние между началом и концом вектора
- 7. Коллинеарные векторыНенулевые векторы называются коллинеарными, если они
- 8. Направление векторовЕсли два ненулевых вектора коллинеарны и
- 9. Направление векторовЕсли два ненулевых вектора коллинеарны и
- 10. Направление векторовЕсли два ненулевых вектора коллинеарны и
- 11. Равенство векторовВекторы называются равными, если они сонаправлены
- 12. Откладывание вектора от данной точкиОт любой точки
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Что такое вектор?
Понятие вектора возникает
там, где приходится иметь дело с объектами, которые характеризуются величиной
и направлением: например, скорость, сила, давление. Такие величины называются векторными величинами или векторами.Слайд 4Геометрическое понятие вектора
Наиболее наглядно величину и направление одновременно можно задать
с помощью направленного отрезка – вектора. Направление вектора указывается стрелкой.
Точка A называется началом вектора, а точка B – концом.Векторы обозначаются латинскими буквами a, b, c, …, а также AB, CD, … (на первом месте ставится начало вектора).
В
А
Начало вектора
Конец вектора
C
D
a
b
c
Слайд 5Нулевой вектор
Любую точку плоскости можно считать вектором. Такой вектор называется
нулевым.
Начало нулевого вектора совпадает с его концом.
Нулевой вектор обозначается 0
или СС.М
С
Слайд 6Длина вектора
Расстояние между началом и концом вектора называется длиной или
модулем вектора. Длина вектора обозначается |а| или |АВ|.
Длина нулевого вектора
считается равной нулю.a
C
D
N
|AB| = 6 |CD| = 5
|a| = 5 |NN| = 0
(каждая клетка на рисунке имеет сторону, равную единице измерения отрезков)
Слайд 7Коллинеарные векторы
Ненулевые векторы называются коллинеарными, если они лежат либо на
одной прямой, либо на параллельных прямых.
Нулевой вектор считается коллинеарным любому
вектору.CD, KF, O, a, b – коллинеарные
O, a – коллинеарные
O, NP – коллинеарные
NP, m – не коллинеарные
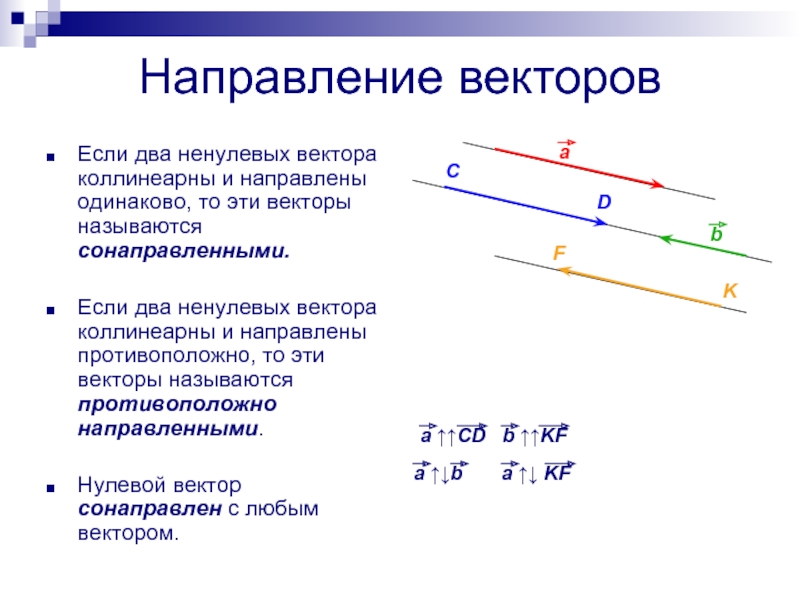
Слайд 8Направление векторов
Если два ненулевых вектора коллинеарны и направлены одинаково, то
эти векторы называются сонаправленными.
Если два ненулевых вектора коллинеарны и направлены
противоположно, то эти векторы называются противоположно направленными.Нулевой вектор сонаправлен с любым вектором.
a ↑↑CD b ↑↑KF
Слайд 9Направление векторов
Если два ненулевых вектора коллинеарны и направлены одинаково, то
эти векторы называются сонаправленными.
Если два ненулевых вектора коллинеарны и направлены
противоположно, то эти векторы называются противоположно направленными.Нулевой вектор сонаправлен с любым вектором.
a ↑↑CD b ↑↑KF
C
D
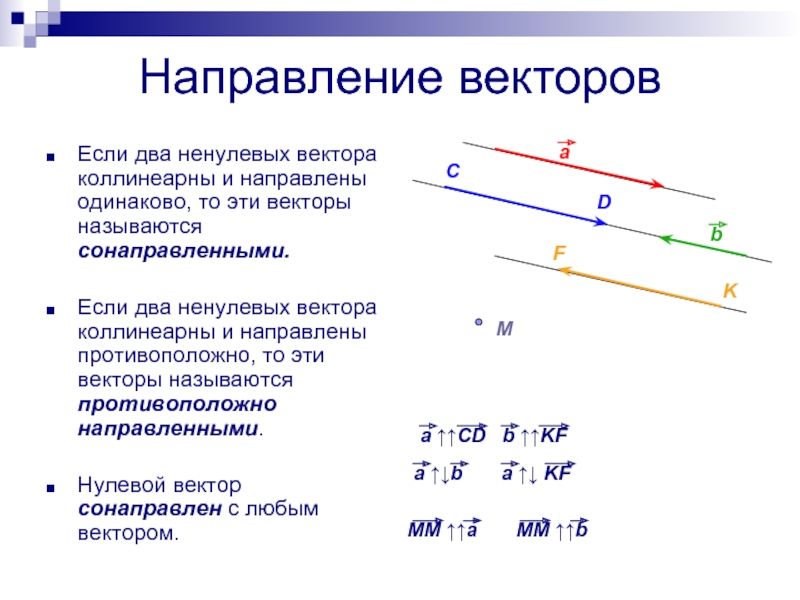
Слайд 10Направление векторов
Если два ненулевых вектора коллинеарны и направлены одинаково, то
эти векторы называются сонаправленными.
Если два ненулевых вектора коллинеарны и направлены
противоположно, то эти векторы называются противоположно направленными.Нулевой вектор сонаправлен с любым вектором.
a ↑↑CD b ↑↑KF
a ↑↓b a ↑↓ KF
a
C
D
Слайд 11Равенство векторов
Векторы называются равными, если они сонаправлены и их длины
равны.
Равенство векторов обозначается: a = b
Все нулевые векторы равны друг
другу.Слайд 12Откладывание вектора от данной точки
От любой точки можно отложить вектор,
равный данному вектору, и притом только один.
а
А
В
М
N'
N
p
M ∈ p
p II
ABMN = AB
MN' = AB
MN = a
Слайд 13
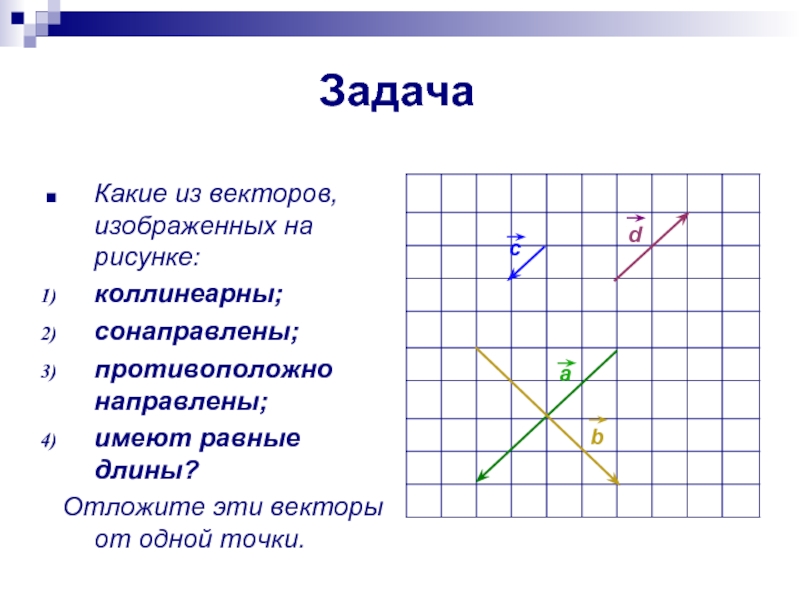
Задача
Какие из векторов, изображенных на рисунке:
коллинеарны;
сонаправлены;
противоположно направлены;
имеют равные длины?
Отложите эти векторы от одной точки.a
b
d
c
Слайд 14
Задача
На рисунке изображена равнобедренная трапеция KLMN.
а) Укажите сонаправленные, противоположно
направленные, равные вектора.б) Укажите векторы, длины которых равны. Равны ли при этом сами векторы?
K
L
M
N
Слайд 15 Задачи
Даны
вектор BC и точка D(1;-2). Отложите от точки D вектор,
равный вектору BC.Как должен быть расположен ненулевой вектор a относительно прямой k, чтобы нашлись лежащие на этой прямой векторы, равные a? Сколько таких векторов найдется? Отметьте на чертеже три из них.
Векторы AB и DC равны. Докажите, что если точки A, B, C и D не лежат на одной прямой, то четырехугольник ABCD ― параллелограмм.
Слайд 16
Задачи
На рисунке изображен параллелограмм ABCD.Укажите векторы, длины которых равны.
Равны ли при этом сами векторы? В ромбе ABCD lACl = 12см, lBDl = 16см. От вершины A отложен вектор AE, равный вектору BD. Найдите длину вектора EC.
Отметьте две точки A и B. Найдите такую точку X, что: а) AX = XB; б) AX = BX; в) XA = XB.