Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вертикальные и смежные углы
Содержание
- 1. Вертикальные и смежные углы
- 2. Теоретический материал Определение . Два угла
- 3. Смежные углыТеорема. Сумма смежных углов равна 180
- 4. Вертикальные углыОпределение. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. АОСВД
- 5. Теорема. Вертикальные углы равны.Доказательство. Пусть углы АОВ
- 6. Решение задач. Задача №1 Определите по рисунку
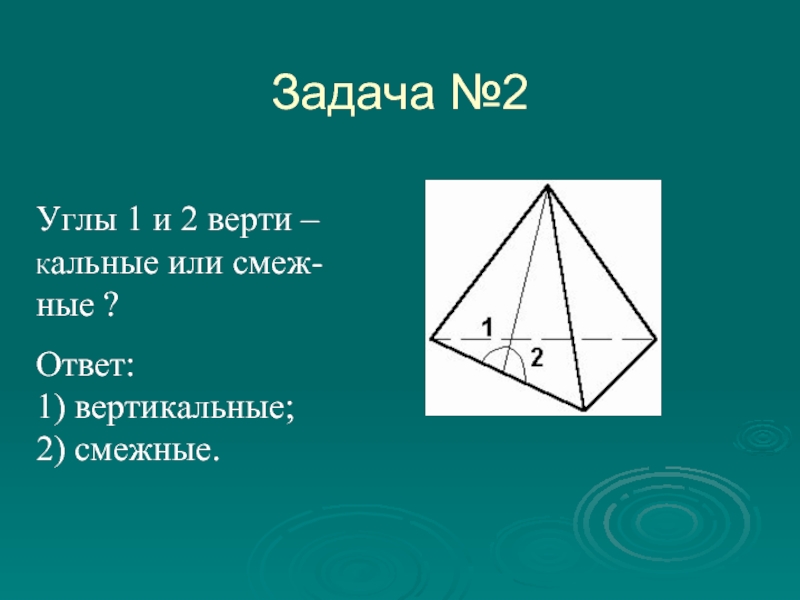
- 7. Задача №2Углы 1 и 2 верти –Кальные
- 8. Решить устно . Задача №1 Угол 2
- 9. Задача №2Угол 2 на 400 меньше угла
- 10. Найти углы 2, 3, 4.Ответ: 1)2
- 11. Углы 1 и 2 – смежные. Угол
- 12. МОЛОДЕЦ !!!
- 13. Правильный ответ : 2) 700 и 1100 Неверно!
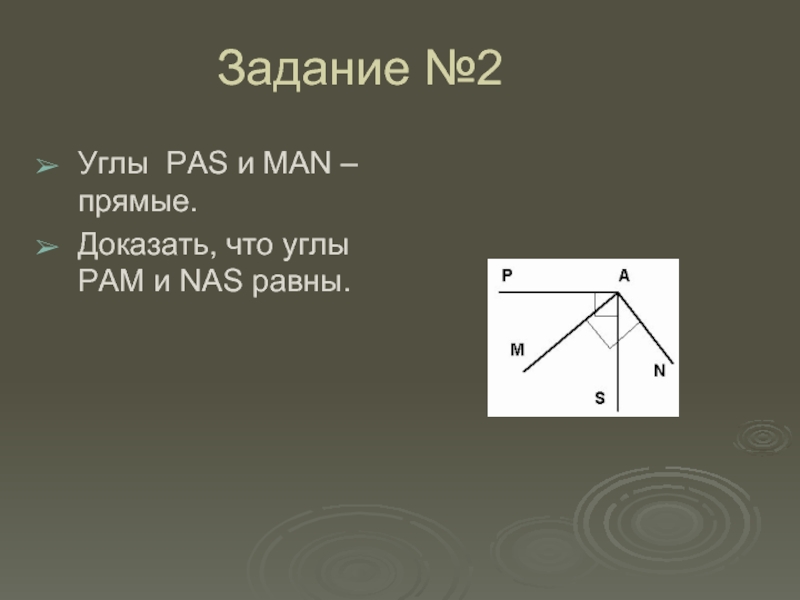
- 14. Задание №2Углы PAS и MAN –прямые.Доказать, что углы PAM и NAS равны.
- 15. Знание данной темы необходимо для дальнейшего изучения геометрии.
- 16. Литература :Варданян С. С.Задачи по
- 17. Скачать презентанцию
Теоретический материал Определение . Два угла называются смежными , если у них одна сторона общая , а другие стороны этих углов являются дополнительными полупрямымиАСВО
Слайды и текст этой презентации
Слайд 2 Теоретический материал
Определение . Два угла называются смежными ,
если у них одна сторона общая , а другие стороны
этих углов являются дополнительными полупрямымиА
С
В
О
Слайд 3Смежные углы
Теорема. Сумма смежных углов равна 180 градусам .
Доказательство .
Пусть АОВ и СОВ – смежные углы . Луч ОВ
проходит между сторонами АО и ОС развернутого угла . Поэтому сумма углов АОВ и СОВ равна развернутому углу , т . е . 180 градусам.Теорема доказана .
Следствие 1. Если два угла равны , то смежные с ними углы равны. .
Следствие 2. Если угол не развернутый , то его градусная мера меньше 180 градусов .
Следствие 3. Угол , смежный с прямым углом , есть прямой угол.
Слайд 4Вертикальные углы
Определение. Два угла называются вертикальными, если стороны одного угла
являются дополнительными полупрямыми сторон другого.
А
О
С
В
Д
Слайд 5Теорема. Вертикальные углы равны.
Доказательство. Пусть углы АОВ и СОД –
вертикальные углы. Угол ДОВ является смежным с углом ДОС и
с углом АОВ. Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов АОВ и СОД дополняет угол ДОВ до 180 градусов, т. е. углы АОВ и СОД равны. Теорема доказана.А
О
С
В
Д
Слайд 6Решение задач. Задача №1
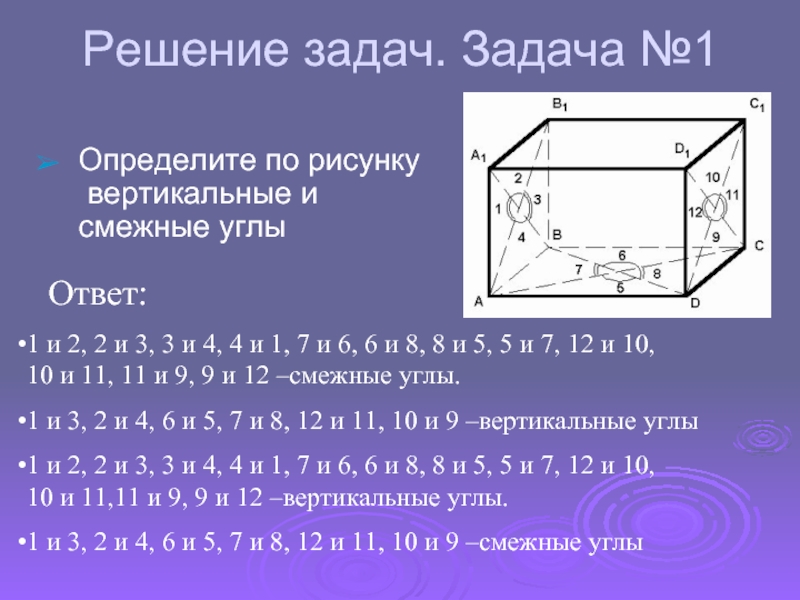
Определите по рисунку
вертикальные и смежные
углы
1 и 2, 2 и 3, 3 и 4, 4
и 1, 7 и 6, 6 и 8, 8 и 5, 5 и 7, 12 и 10,
10 и 11, 11 и 9, 9 и 12 –смежные углы.1 и 3, 2 и 4, 6 и 5, 7 и 8, 12 и 11, 10 и 9 –вертикальные углы
1 и 2, 2 и 3, 3 и 4, 4 и 1, 7 и 6, 6 и 8, 8 и 5, 5 и 7, 12 и 10, 10 и 11,11 и 9, 9 и 12 –вертикальные углы.
1 и 3, 2 и 4, 6 и 5, 7 и 8, 12 и 11, 10 и 9 –смежные углы
Ответ:
Слайд 8Решить устно . Задача №1
Угол 2 на 300 больше
угла 1.
Найдите эти углы.
Ответ :
1)600 и 1200 2) 7500 и 1050 3) 1000 и 800
2
1
Слайд 9Задача №2
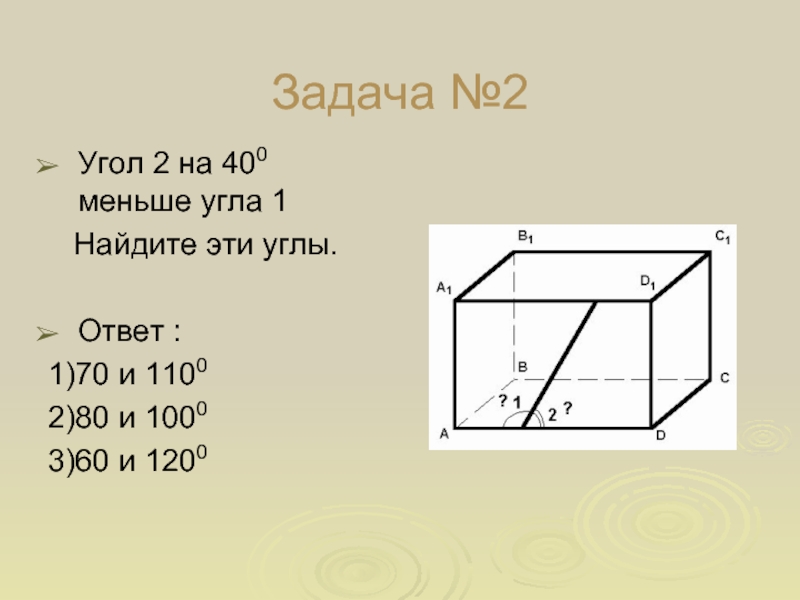
Угол 2 на 400 меньше угла 1
Найдите
эти углы.
Ответ :
1)70 и 1100
2)80 и 1000
3)60 и 1200
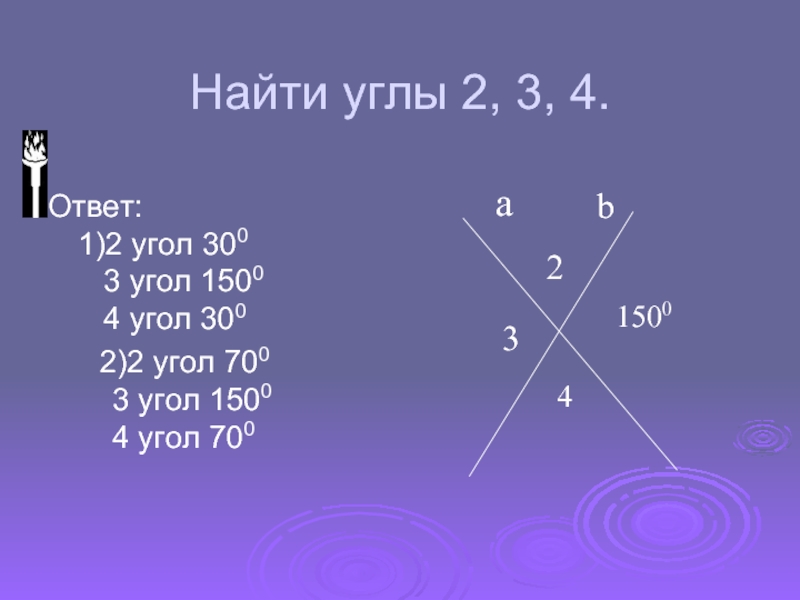
Слайд 10Найти углы 2, 3, 4.
Ответ:
1)2 угол 300
3
угол 1500
4 угол 300
2)2 угол
700
3 угол 1500
4 угол 700а
b
1500
2
4
3
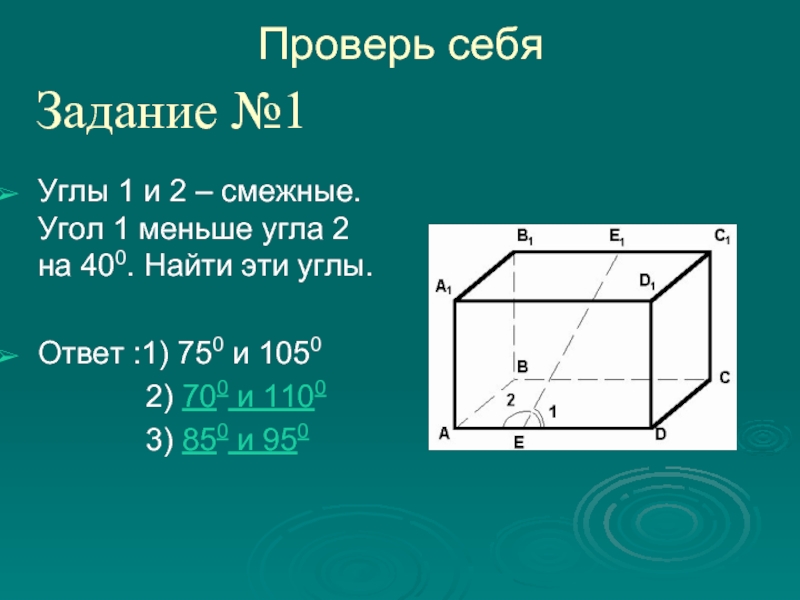
Слайд 11Углы 1 и 2 – смежные. Угол 1 меньше угла
2
на 400. Найти эти углы.
Ответ :1) 750 и 1050
2) 700 и 1100 3) 850 и 950
Задание №1
Проверь себя
Слайд 16Литература :
Варданян С. С.Задачи по
планиметрии с практическим содержанием
Погорелов А. В.
Геометрия ,7 – 11.Болтянский В. Д. , Глейзер Г. Геометрия 7 -8.
Теги