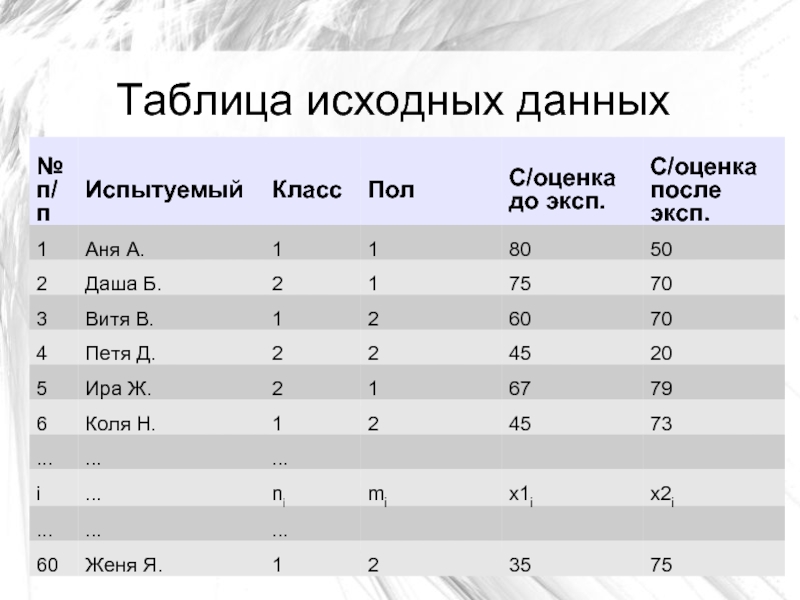
Слайд 1Математические основы описания результатов исследования
Слайд 3Группировка данных
Группировка — процесс систематизации и упорядочивания данных с целью
извлечения содержащейся в них информации
Способы группировки:
А) безинтервальный вариационный ряд;
Б)
интервальный вариационный ряд.
Данные могут быть представлены в аналитической и графической форме
Слайд 4Вариационный ряд: термины
Вариационный ряд — ранжированный в порядке возрастания/убывания ряд
значений признака с соответствующими им весами (количествами людей, обладающих этим
уровнем признака).
1) Дискретный вариационный ряд — частоты привязаны к конкретным значениям признака.
Пример: у 5 детей по тесту школьной готовности 10 баллов; 3 ребенка получили 7 баллов; 4 ребенка — 8 баллов; и один ребенок — 5 баллов.
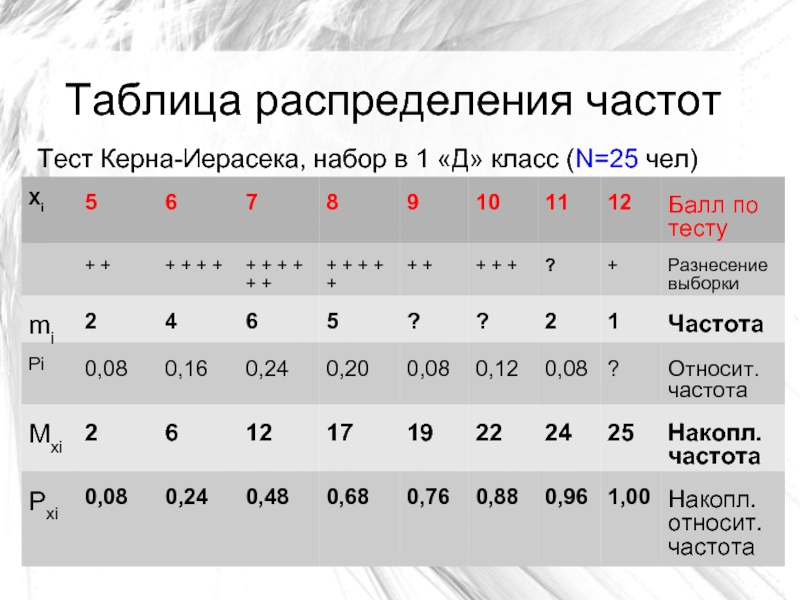
Слайд 5Таблица распределения частот
Тест Керна-Иерасека, набор в 1 «Д» класс (N=25
чел)
Слайд 6Определения
Частота - число, показывающее, сколько раз данное значение признака встречается
в данной выборке.
Относительная частота — отношение частоты к объему выборки
Накопленная частота — сумма частот от первого имеющегося значения до текущего
Накопленная относительная частота — аналогично см. выше
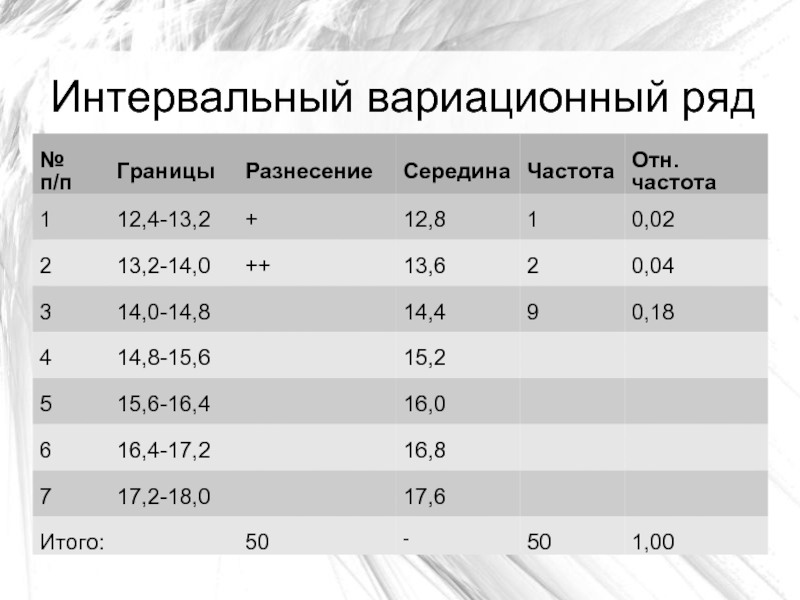
Слайд 8Интервальный вариационный ряд
В интервальном вариационном ряду частоты, характеризующие повторяемость вариантов
в выборке, распределяются по интервалам группировки;
Применяется, если:
а) есть большой размах
вариации;
б) объем выборки большой;
в) измеряли непрерывную величину (время, скорость и т.п.)
Слайд 9Интервальный вариационный ряд
Количество интервалов - по формуле Стерджеса, в которой
k - число интервалов, N-объем выборки
k=1+3,32*lgN
Количество интервалов - по таблице:
Слайд 10Интервальный вариационный ряд
Ширина интервала определяется по формуле:
h=(Хмах- Хmin)/k
Есть два правила:
Правило
1. Точность границ интервала должна быть равна точности данных (число
знаков после запятой одинаково)
Правило 2. Минимальное значение должно попадать в середину 1-го интервала
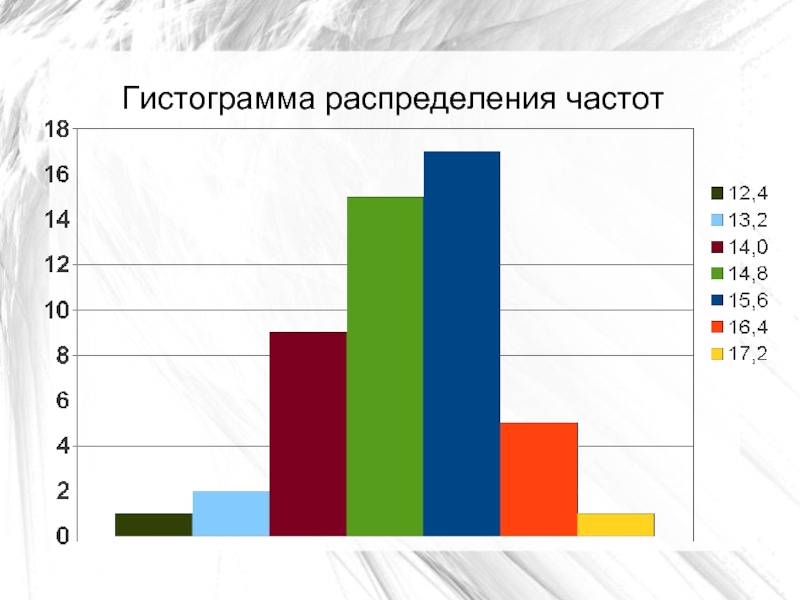
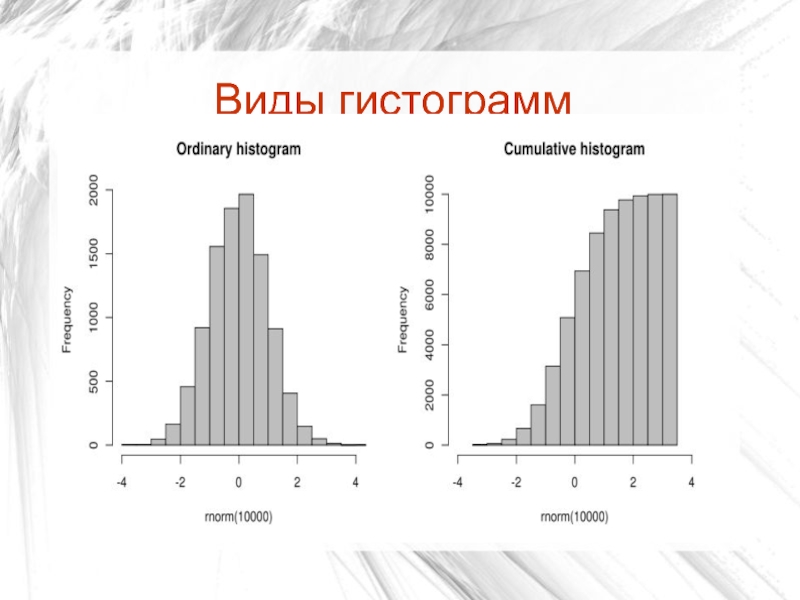
Слайд 12Гистограмма распределения частот
Слайд 13Гистограмма
Гистограмма — график, отображающий особенности интервального ряда распределения (термин ввел
К.Пирсон в 1895г.)
Основанием столбика диаграммы является интервал группировки
При построении гистограммы,
описывающей плотность распределения, высота i-го столбика (L) зависит от частоты (m) данного интервала:
Li = mi / (h*N)
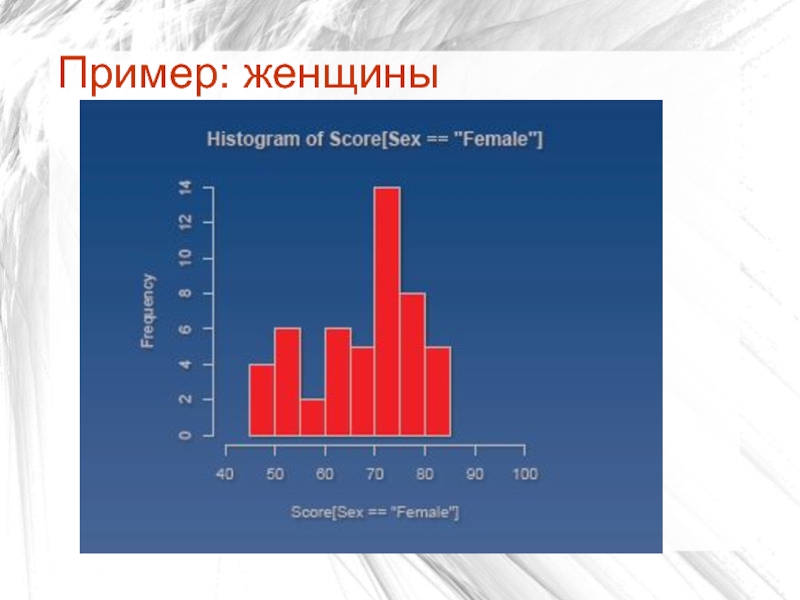
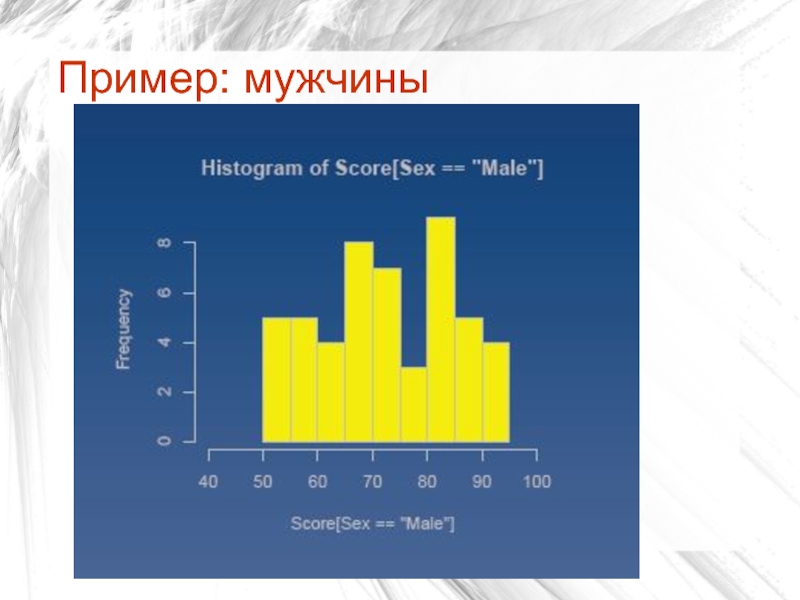
Слайд 15Для чего нужны гистограммы?
Понять истинную природу различий двух выборок
Пример:
50 мужчин
и 50 женщин;
1 тест пространственного мышления (0-100);
Мужчины: ср.арифм=72,62
Женщины: ср.арифм=67,92
Слайд 19Для чего нужны гистограммы?
Понять, есть ли скрытые переменные
Пример:
Влияет ли оральная
контрацепция на уровень Артериального Давления (АД)?
100 женщин, использующих “The Pill”
100
женин, использующих другие виды контрацепции
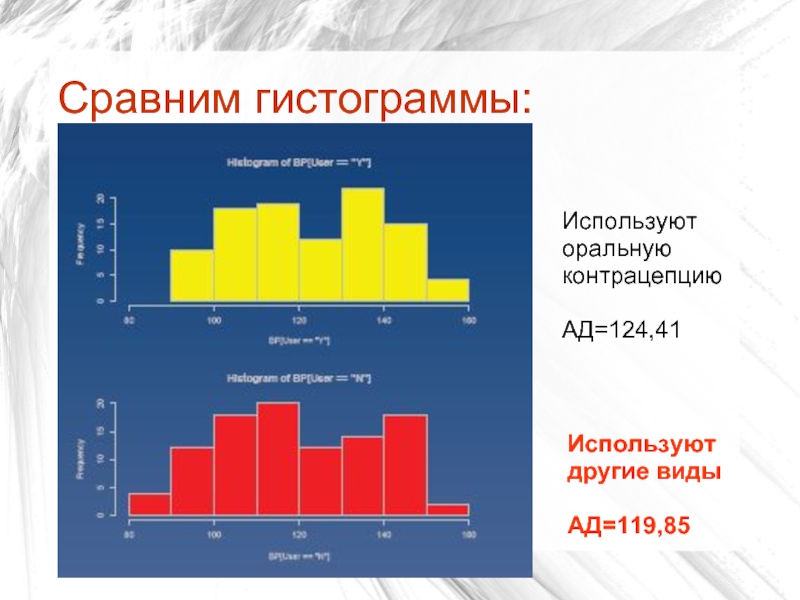
Слайд 20Сравним гистограммы:
Используют оральную контрацепцию
АД=124,41
Используют другие виды
АД=119,85
Слайд 21Задание
Возраст рабочих цеха (в годах):
18; 38; 40; 28; 29;
26; 38; 34; 22; 28; 30; 22; 23; 35; 33;
27; 24; 30; 32; 49; 37; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29; 52; 58; 44; 39; 57; 19; 25.
Для анализа распределения рабочих цеха по возрасту требуется:
1. Построить интервальный ряд распределения;
2. Дать графическое изображение ряда. Сформулировать вывод.