Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Внеклассное мероприятие "Хочу все знать!" 8 класс
Содержание
- 1. Внеклассное мероприятие "Хочу все знать!" 8 класс
- 2. Умницы 8 класса Умницы 8 Г класса
- 3. Цели мероприятия1. Развитие познавательной
- 4. На доскеПродолжается
- 5. Ход мероприятия1. Выбирается жюри,
- 6. Вопросы1. Некоторые
- 7. Вопросы3. Немецкого
- 8. Вопросы7.
- 9. Вопросы11.
- 10. Вопросы15. У
- 11. Супер – игра.
- 12. Рекламная пауза Показать,
- 13. Зеленая дорожка1. Куб,
- 14. Желтая дорожка1. Куб,
- 15. Красная дорожка1. Куб,
- 16. РезультативностьВ ходе мероприятия развиваются познавательная активность, творческие способности, самостоятельность, логическое мышление, Упорство, трудолюбие, толерантность.
- 17. Проведено в 8 классе учителем Скурлатовой О.
- 18. Скачать презентанцию
Умницы 8 класса Умницы 8 Г класса
Слайды и текст этой презентации
Слайд 3 Цели мероприятия
1. Развитие познавательной активности и творческих
способностей;
2. Развитие самостоятельности, логического мышления;
3. Развитие упорства, трудолюбия, толерантности.
Слайд 4 На доске
Продолжается век.
И другой приближается
век.
По кремнистым ступеням
взбираясь к опасным вершинам,
никогда, никогда, никогда
не отдаст человек
своего
превосходстваумнейшим на свете машинам.
(П. Антокольский)
Слайд 5 Ход мероприятия
1. Выбирается жюри, состоящее из двух
человек, которые следят за тем, кто первым готов дать ответ,
раздают ордена умникам за правильный ответ и следят за временем (т. к. некоторые вопросы даются на время, например в супер – игре).2. Ведущий (учитель) работает со всем классом, задает вопросы. Правильно ответивший, получает орден. В супер – игру выходят 3 ученика, набравшие наибольшее количество орденов.
Слайд 6 Вопросы
1. Некоторые жители африканских джунглей
любят соревноваться в прыжках в высоту, по типу батута. Находят
лесную поляну, застилают ветками и листьями толщиной до 1,5 м. С верхушек окружающих поляну деревьев участники прыгают на пружинящий растительный ковер и подскакивают, как на батуте. Кто считается победителем? (Кто сумеет не только высоко подпрыгнуть, но и ухватиться за ветку дерева)2. Я железнодорожная кассирша, продаю билеты. Многим это кажется очень простым делом. Необходимо, чтобы пассажиры могли получить билеты от данной станции до любой другой на этой же дороге, иногда и туда и обратно. Я служу на дороге с 25 станциями. Сколько же, по-вашему, различных образцов билетов заготовлено железной дорогой для всех ее касс? (2∙25∙24=1200)
Слайд 7 Вопросы
3. Немецкого математика называли королем
математиков. В 3-х летнем возрасте он делал поправки при расчетах.
Кто он? (К. Гаусс)4. Найти наименьшее число, которое при делении на 2 дает в остатке 1, при делении на 3 – 2, на 4 – 3. (11)
5. Сколько существует целых положительных двузначных чисел? (90)
6. Позавчера мне было 10 лет, а в будущем году исполнится 13 лет. Когда же день моего рождения и день разговора? (День рождения – 31 декабря, день разговора – 1 января)
Слайд 8 Вопросы
7. В одном ящике
лежат 10 пар коричневых, 10 пар черных носков, в другом
– 10 пар черных перчаток, 10 пар коричневых. По сколько носков и перчаток достаточно извлечь из каждого ящика, чтобы из них можно было выбрать одну (какую-либо) пару носков и одну пару перчаток? (3 носков и 21 перчатку)8. Один отец дал своему сыну 150 рублей, а другой своему – 100 рублей. Оказалось, что оба сына вместе увеличили свои капиталы на 150 рублей. Чем это объяснить? (Дед→отец→сын
9. Выразить 1, употребив все 10 цифр. (123456789⁰, )
10. Сообразите в уме: на сколько км возвышался бы столб, составленный из всех миллиметровых кубиков одного м³, положенных один на другой (1000км)
Слайд 9 Вопросы
11. Изделие весит 89,4г.
Сообразите в уме, сколько тонн весит миллион таких изделий? (89,4т)
12.
Продолжи ряд: О; Д; Т; Ч; П; Ш; … (С; В; Д.) (один, два,…)13. Каким должно быть число, чтобы 1/10 процента от него =1/10? (100)
14. Где ошибка? 1=2?
1-3=4-6;
1-3+9/4=4-6+9/4;
(1-3/2) ² =(2-3/2)²;
(1-3/2)² = ( 2-3/2)²;
1-3/2=2-3/2;
1=2. ( (1-3/2)² =׀1-3/2׀, ( 2-3/2)² =׀ (2-3/2)׀)
Слайд 10 Вопросы
15. У мальчика столько сестер,
сколько братьев, а у его сестры вдвое меньше сестер, чем
братьев. Сколько братьев и сестер в этой семье? (4 брата, 3 сестры)16. Найдите число, если полтрети его – число 100. (600)
33 44
17. Записать наибольшее число при помощи 3-х троек, 3-х четверок. (3 ;4 )
18. Четыре яблока, не разрезая их, нужно разделить между тремя приятелями так, чтобы никто из них не получил больше, чем остальные. Как это сделать?
(2; 1; 1)
19. На какое число нужно разделить 2, чтобы получить 4? (1/2)
5 5-5
20. Записать, пользуясь тремя пятерками и знаками действий «1». ((5׃5); 5 )
21. Когда делимое и частное равны между собой? (Делитель равен 1)
Слайд 11 Супер – игра.
3 дорожки:
Зеленая – допускается 2 ошибки.
Желтая – допускается 1 ошибка.
Красная – ни одной ошибки.
В супер – игре участвуют трое детей, набравших наибольшее количество орденов. Первым выбирает дорожку тот, кто за 1 минуту напишет большее количество математических терминов, начинающихся на букву «п».
Слайд 12 Рекламная пауза
Показать, как можно графически изображать
пословицы и поговорки:
1. «Как аукнется, так и откликнется».
отклик = ауканью
(биссектриса 1-ого и 3-огокоординатных углов)
2. «Светит да не греет». (одна из полуосей)
3. «Ни кола, ни двора» (точка пересечения координатных осей)
Слайд 13 Зеленая дорожка
1. Куб, длина ребра которого
3см, покрашен краской. Его разрезали на кубики по 1см³. Сколько
кубиков имеют 3 красные грани? (8)2. Стороны прямоугольника выражаются натуральными числами. Какой
длины должны они быть, чтобы значение периметра равнялось значению
его площади? (3 и 6)
3. 4 человека обменялись фотографиями. Сколько было рукопожатий? (6)
4. С помощью четырех «9» и знаков действий записать 100.(99+9/9)
Слайд 14 Желтая дорожка
1. Куб, длина ребра которого
3см, покрашен краской. Его разрезали на кубики по 1см³. Сколько
кубиков имеют 2 красные грани? (12)2. 4 единицами записать самое большее
11
число. (11 )
3. Двумя цифрами и знаками действий записать наименьшее целое положительное число.
0
(1-0; 2-1; 2 ; 3/3; 2/2)
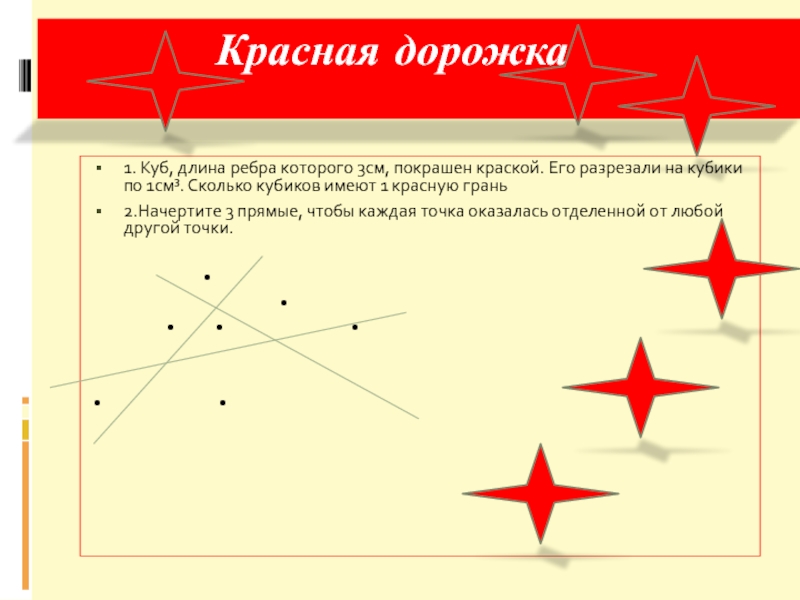
Слайд 15 Красная дорожка
1. Куб, длина ребра которого
3см, покрашен краской. Его разрезали на кубики по 1см³. Сколько
кубиков имеют 1 красную грань2.Начертите 3 прямые, чтобы каждая точка оказалась отделенной от любой другой точки.
•
•
• • •
• •