Слайд 1
Творческая работа по математике
Решение старинных задач различными способами
Слайд 2Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся
задачей. Она может встретиться и на школьном уроке, и на
занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений.
Введение
Слайд 3Старинные задачи позволяют не только развить смекалку и сообразительность, но
и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так
же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.
Слайд 4Еще в древние века математика занимала основное место в умах
ученых и благодаря сохранившимся рукописям у нас есть возможность проследить
за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением.
Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач.
Задачи исследования:
исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом
исследовать старинный способ решения задач на сплавы и смеси.
Слайд 5Диофант
Его называют
отцом алгебры
Диофант умел решать
очень сложные уравнения,
он применял для
этого
буквенные обозначения
и другие приемы.
Биографические данные
зашифрованы в виде
математической задачи,
начертанной
на его гробнице.
Слайд 6Задача № 1
Жизнь Диофанта. По преданию, на могильном камне имелась
такая надпись:
«Путник! Под этим камнем покоится прах Диофанта, умершего в
глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?»
Слайд 12Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой
или наблюдать испарение воды. В задачах такого типа эти операции
приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого.
Слайд 13 Лео́нтий Фили́ппович Магни́цкий
(9(19)июня
1669- 19(30)октября 1739)
Магницкий Л.Ф. (при рождении Телятин)-
русский математик, педагог;
преподаватель математики в Школе
математических и навигацких наук
в Москве (с 1701 по 1739),
автор первой в России учебной
энциклопедии по математике
(в 1703г. «Арифметика»), которая
более ста лет являлась основным
учебным пособием по математике
в России.
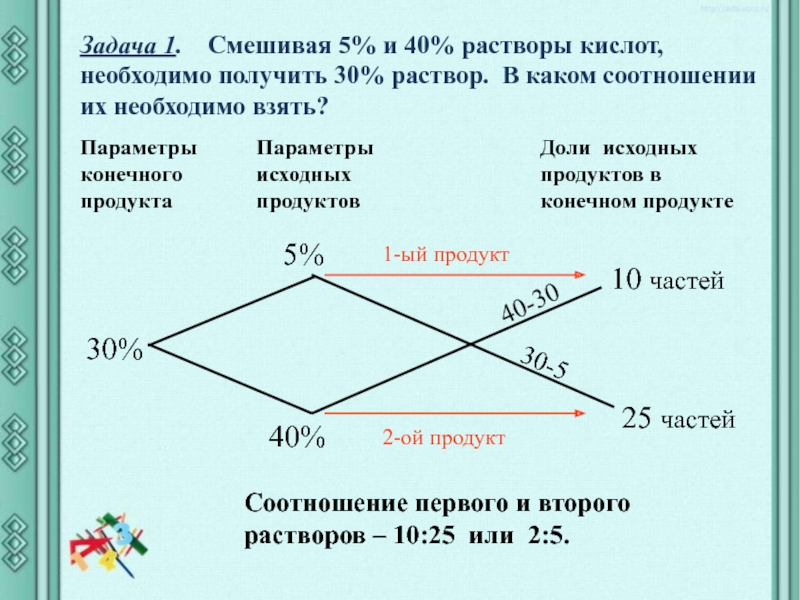
Слайд 14Задача 1. Смешивая 5% и 40% растворы кислот, необходимо
получить 30% раствор. В каком соотношении их необходимо взять?
Параметры
конечного продукта
Параметры исходных продуктов
Доли исходных продуктов в конечном продукте
30%
5%
40%
40-30
30-5
1-ый продукт
2-ой продукт
10 частей
25 частей
Соотношение первого и второго растворов – 10:25 или 2:5.
Слайд 15Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить
30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить
140 г
30%- ого раствора?
Решение:
Сколько всего частей?
2 + 5 = 7(ч)
Сколько грамм приходится на одну часть?
140 : 7 = 20(г)
Сколько грамм 5%-го раствора взять?
2 · 20 = 40(г)
Сколько грамм 40%-го раствора взять?
5 · 20 = 100(г)
Ответ: для получения 140г 30%-ного раствора нужно
взять 5%-ного раствора 40г, а 40%-ного - 100 г.
Слайд 16
Заключение
Математика в настоящее время все шире проникает в повседневную
жизнь, все более внедряется в традиционно далекие от нее области.
Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.
Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор.
«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич)
.
Слайд 17
Ознакомление с историческими фактами
позволяет лучше понять роль математики в современном обществе, углубляют понимание
изучаемого раздела программы.
В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу.