Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на производную
Содержание
- 1. Задачи на производную
- 2. Задача №1 На рисунке изображен график функции y=f(x), определенной
- 3. Решение:первое, на что мы обращаем внимание -
- 4. На рисунке изображен график y=f(x)
- 5. Решение:Значение производной функции f(x) в точке касания
- 6. Задача №3 На рисунке изображен график y
- 7. Решение:Если график y = f'(x) производной функции
- 8. Задача №4На рисунке изображен график функции y=f'(x)
- 9. На отрезке [-5;-1] производная f'(x) принимает отрицательные
- 10. Задача №5 На рисунке изображен график функции
- 11. График производной пересекает ось Ox в точке
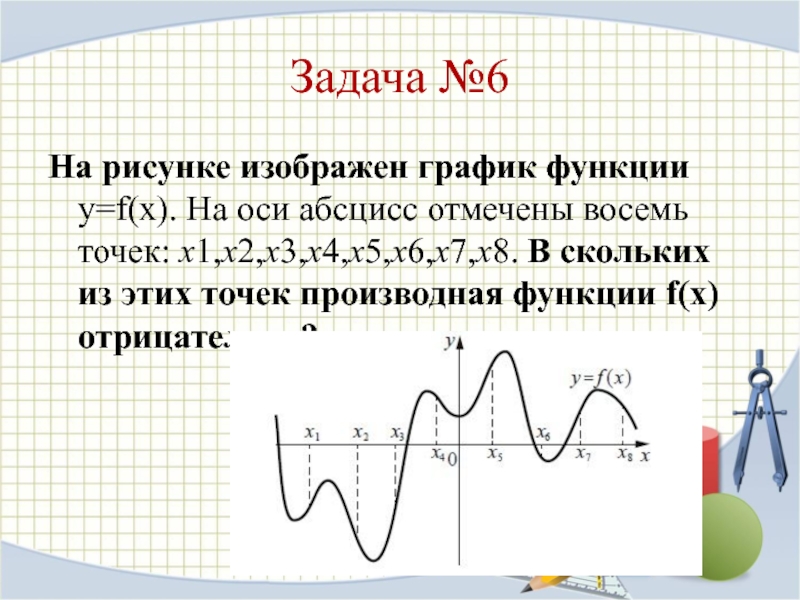
- 12. Задача №6На рисунке изображен график функции y=f(x).
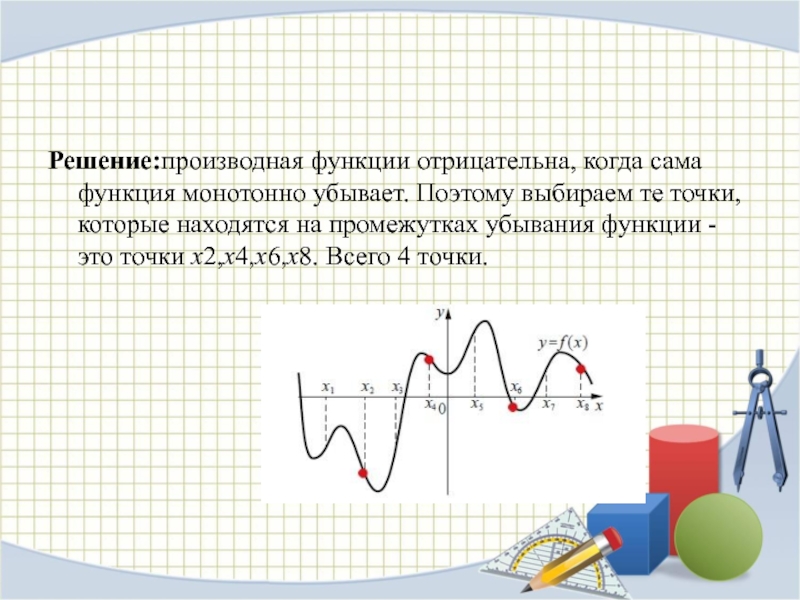
- 13. Решение:производная функции отрицательна, когда сама функция монотонно
- 14. Задача №7 На рисунке изображен график функции
- 15. Решение:точками экстремума функции являются точки пересечения графика
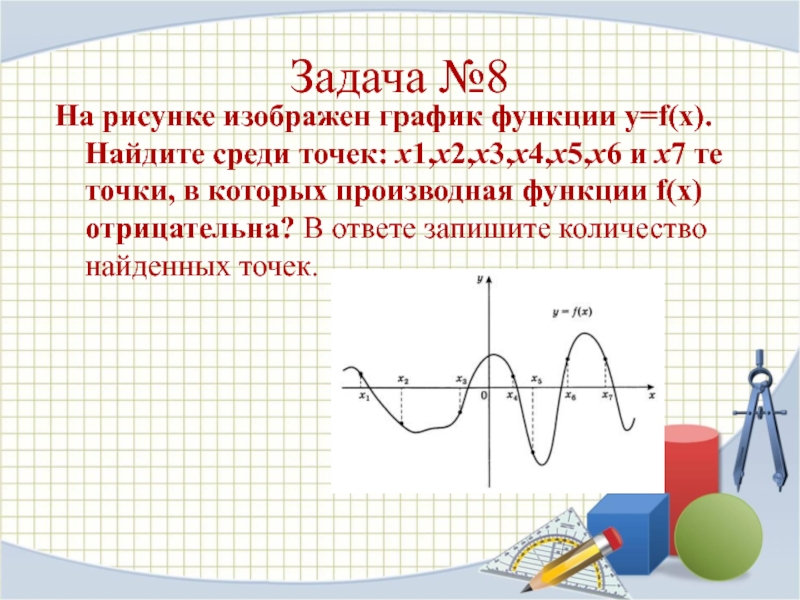
- 16. Задача №8На рисунке изображен график функции y=f(x).
- 17. Решение: производная функции отрицательна, когда сама функция
- 18. Задача №9На рисунке изображены график функции y=f(x)
- 19. Найдем производную функции y=−1/4f(x)+5в точке x0:y′=−1/4f′(x0)Так как
- 20. Задача №10 На рисунке изображен график функции
- 21. Решение:Пусть уравнение касательной к графику функции
- 22. Сайт: http://pedsovet.su/ http://mathexam.ru/b8/b8_5.html
- 23. Скачать презентанцию
Слайды и текст этой презентации
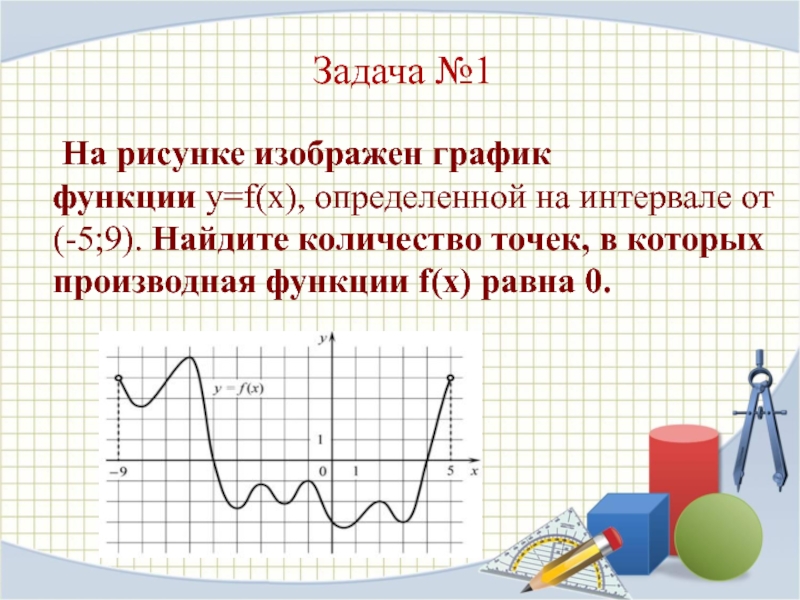
Слайд 2Задача №1
На рисунке изображен график функции y=f(x), определенной на интервале от
(-5;9). Найдите количество точек, в которых производная функции f(x) равна 0.
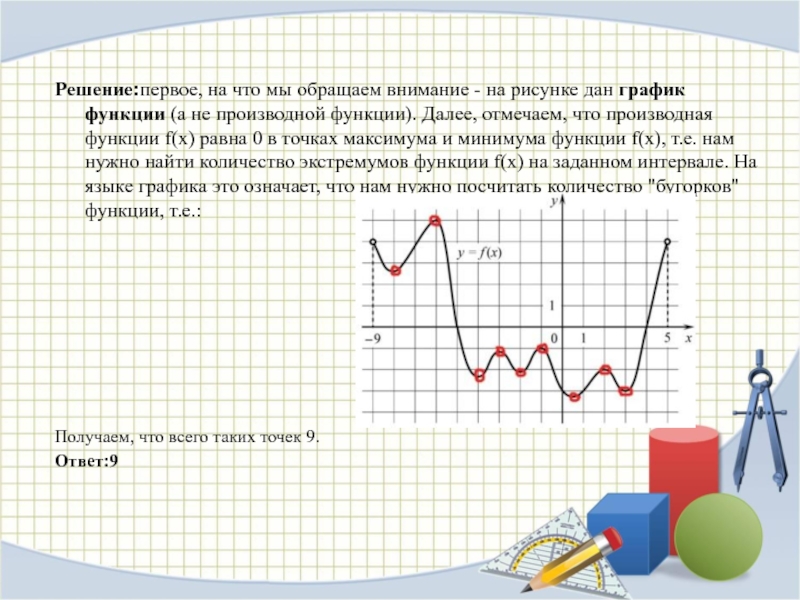
Слайд 3Решение:первое, на что мы обращаем внимание - на рисунке дан график
функции (а не производной функции). Далее, отмечаем, что производная функции f(x)
равна 0 в точках максимума и минимума функции f(x), т.е. нам нужно найти количество экстремумов функции f(x) на заданном интервале. На языке графика это означает, что нам нужно посчитать количество "бугорков" функции, т.е.:Получаем, что всего таких точек 9.
Ответ:9
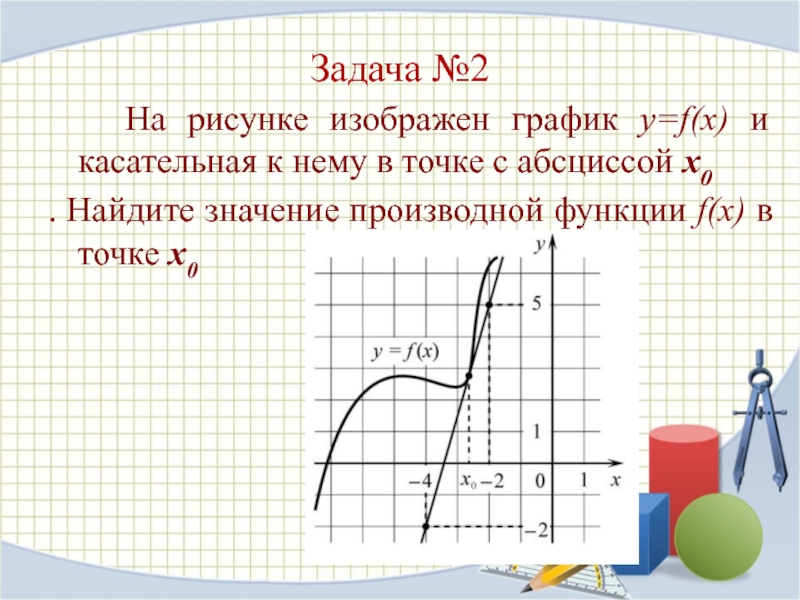
Слайд 4 На рисунке изображен график y=f(x) и касательная к
нему в точке с абсциссой х0
. Найдите значение производной функции
f(x) в точке х0Задача №2
Слайд 5
Решение:Значение производной функции f(x) в точке касания равно угловому коэффициенту
касательной. Поэтому нам надо составить уравнение данной касательной и графику
и найти угловой коэффициент. В общем случае, уравнение касательной имеет вид: y = kx+b. В этом уравнении k и есть тот самый угловой коэффициент, который мы будет искать.На рисунке жирными точками отмечены точки, через которые проходит наша касательная. Координаты этих точек: (-4; -2) и (-2; 5). Так как данная прямая проходит через эти точки, то подставим их координаты в уравнение касательной и найдем значение коэффициента k. y = kx+b
-2 = -4k+b (подставили точку с координатами (-4;-2));
5 = -2k+b (подставили точку с координатами (-2;5)).
Теперь вычитаем из первого уравнения второе:
-2 - 5 = -4k-(-2k);
-7 = -2k;
k = 7/2 = 3,5.
Получаем искомое значение k=3,5, что то же самое, что значение производной функции f(x) в точке x_0.
Ответ: 3,5.
.
y = kx+b
-2 = -4k+b (подставили точку с координатами (-4;-2));
5 = -2k+b (подставили точку с координатами (-2;5)).
Теперь вычитаем из первого уравнения второе:
-2 - 5 = -4k-(-2k);
-7 = -2k;
k = 7/2 = 3,5.
Получаем искомое значение k=3,5, что то же самое, что значение производной функции f(x) в точке .
Ответ: 3,5.
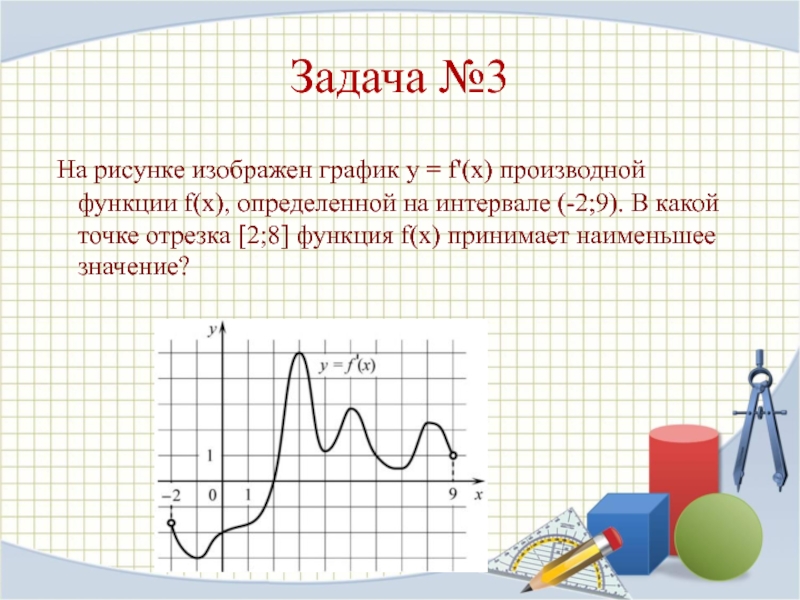
Слайд 6Задача №3
На рисунке изображен график y = f'(x) производной
функции f(x), определенной на интервале (-2;9). В какой точке отрезка
[2;8] функция f(x) принимает наименьшее значение?Слайд 7
Решение:Если график y = f'(x) производной функции f(x) пересекает ось
Ox в некоторой точке, то функция f(x) в этой точке
имеет максимум или минимум. В данном случае график y = f'(x) перескает ось Ox в точке x=2. Так как при x<2 функция y = f'(x) <0 (это видно из графика), а при x>2 y = f'(x)>0 на рассматриваемом графике, то знак производной переходит с "-" на "+". А это означает, что x=2 - точка минимума. И т.к. x=2 принадлежит отрезку [2;8], то x=2 - искомая точка, в которой функция принимает наименьшее значение.Ответ: 2.
Ответ
Слайд 8Задача №4
На рисунке изображен график функции y=f'(x) - производной функции
f(x), определенной на интервале от (-6;5). В какой точке отрезка
[-5;-1] функция f(x) принимает наибольшее значение?Слайд 9
На отрезке [-5;-1] производная f'(x) принимает отрицательные значения, а значит
на этом отрезке функция f(x) убывает. Если функция убывает на
заданном отрезке, то наибольшее значение она принимает в наименьшей точке отрезка, т.е. в точке -5.Ответ: -5.
Слайд 10Задача №5
На рисунке изображен график функции y=f'(x) - производной
функции f(x), определенной на интервале от (-6;5). В какой точке
отрезка [-3;4] функция f(x) принимает наибольшее значение?.Слайд 11
График производной пересекает ось Ox в точке -1. Эта точка
принадлежит отрезку [-3;4] и является точкой экстремума функции f(x).
Ответ: -1.
Так
как график производной переходит в этой точке с "+" на "-", то это точка максимума, а значит наибольшее значение на отрезке [-3;4] функция f(x) принимает именно в этой точке.Слайд 12Задача №6
На рисунке изображен график функции y=f(x). На оси абсцисс
отмечены восемь точек: x1,x2,x3,x4,x5,x6,x7,x8. В скольких из этих точек производная
функции f(x) отрицательна?Слайд 13
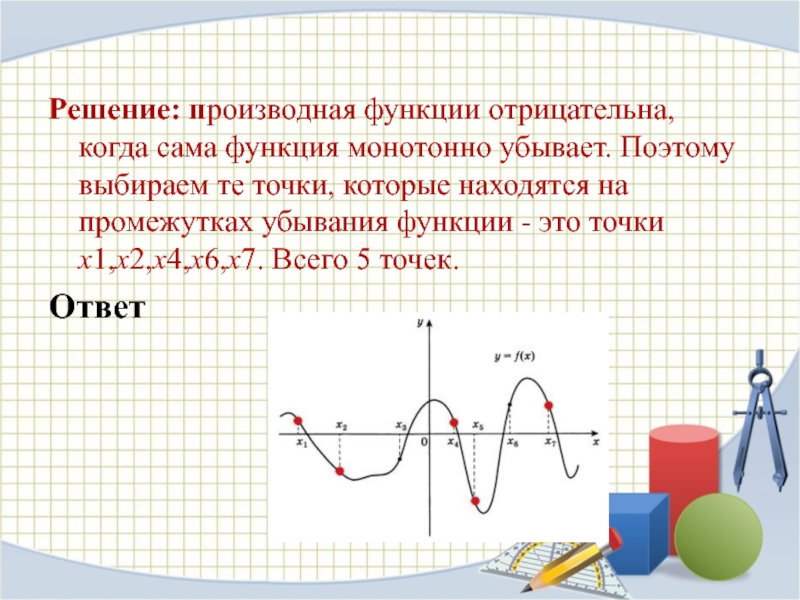
Решение:производная функции отрицательна, когда сама функция монотонно убывает. Поэтому выбираем
те точки, которые находятся на промежутках убывания функции - это
точки x2,x4,x6,x8. Всего 4 точки.Слайд 14Задача №7
На рисунке изображен график функции y=f'(x) - производной
функции f(x), определенной на интервале от (-7;5). Найдите точку экстремума
функции f(x), принадлежащую отрезку [-6;4].Слайд 15
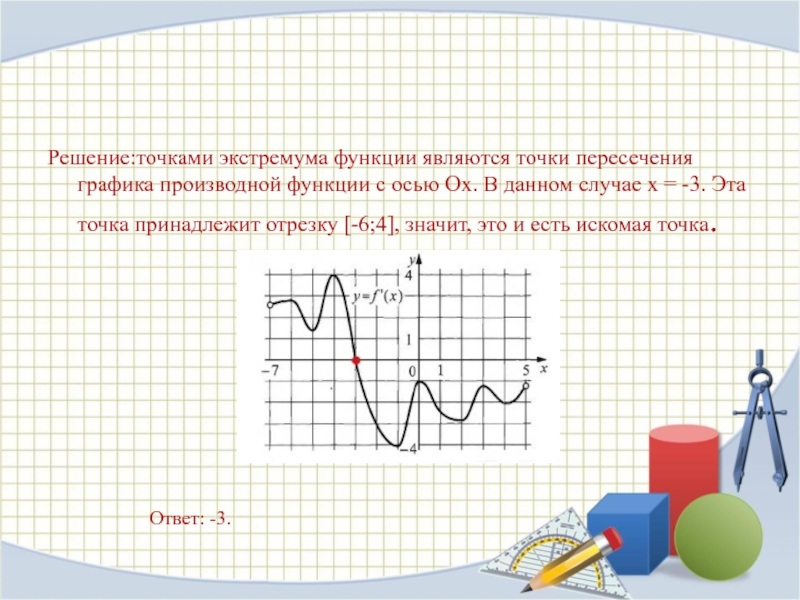
Решение:точками экстремума функции являются точки пересечения графика производной функции с
осью Ox. В данном случае x = -3. Эта точка
принадлежит отрезку [-6;4], значит, это и есть искомая точка.Ответ: -3.
Слайд 16Задача №8
На рисунке изображен график функции y=f(x). Найдите среди точек:
x1,x2,x3,x4,x5,x6 и x7 те точки, в которых производная функции f(x)
отрицательна? В ответе запишите количество найденных точек.Слайд 17
Решение: производная функции отрицательна, когда сама функция монотонно убывает. Поэтому
выбираем те точки, которые находятся на промежутках убывания функции -
это точки x1,x2,x4,x6,x7. Всего 5 точек.Ответ
Слайд 18Задача №9
На рисунке изображены график функции y=f(x) и касательная к
этому графику, проведенная в точке x0. Уравнение касательной показано на
рисунке. Найдите значение производной функции y=−1/4f(x)+5 в точке x0.Слайд 19
Найдем производную функции y=−1/4f(x)+5в точке x0:
y′=−1/4f′(x0)
Так как уравнение касательной к
функции f(x) в точке x0
имеет вид: y = -2x+5, то
f′(x0)=−2.Тогда искомая производная равна:
y' = −1/4⋅(−2)=0,5.
Ответ: 0,5.
Слайд 20Задача №10
На рисунке изображен график функции y=f'(x) - производной
функции f(x), определенной на интервале (-10; 2). Найдите количество точек,
в которых касательная к графику функции f(x) перпендикулярна прямой y = -2x-11.Слайд 21
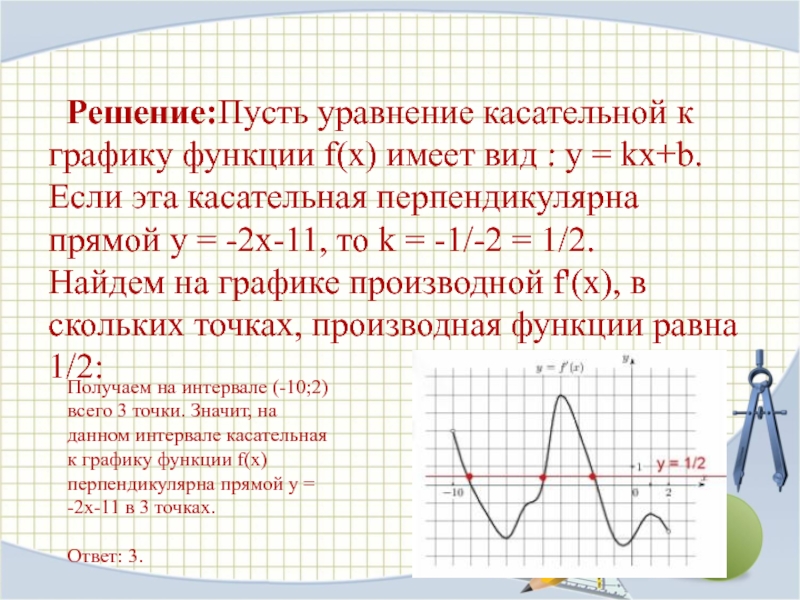
Решение:Пусть уравнение касательной к графику функции f(x) имеет вид
: y = kx+b.
Если эта касательная перпендикулярна прямой y =
-2x-11, то k = -1/-2 = 1/2.Найдем на графике производной f'(x), в скольких точках, производная функции равна 1/2:
Получаем на интервале (-10;2) всего 3 точки. Значит, на данном интервале касательная к графику функции f(x) перпендикулярна прямой y = -2x-11 в 3 точках.
Ответ: 3.




![Задачи на производную На отрезке [-5;-1] производная f'(x) принимает отрицательные значения, а значит на На отрезке [-5;-1] производная f'(x) принимает отрицательные значения, а значит на этом отрезке функция f(x) убывает. Если](/img/thumbs/e603697de3f84dee6b24860230ee0819-800x.jpg)

![Задачи на производную График производной пересекает ось Ox в точке -1. Эта точка принадлежит График производной пересекает ось Ox в точке -1. Эта точка принадлежит отрезку [-3;4] и является точкой экстремума](/img/thumbs/85ead416ef00ec3370d8706ab3f069d0-800x.jpg)