Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на смекалку для 5-6 классов
Содержание
- 1. Задачи на смекалку для 5-6 классов
- 2. На дворе бегают куры и поросята. У
- 3. Решение№1:52-20*2=12 (ног) –поросят12:2=6 – поросят20-6=14- кур
- 4. В клетке находтся фазаны и кролики. у
- 5. И у фазанов и у кроликов по
- 6. Беседуют трое: Белокуров, Чернов и Рыжов. Брюнет
- 7. Решение№3:Беседуют трое: Белокуров, Чернов и Рыжов. Брюнет
- 8. Имеется три коробочки: синяя, желтая и белая.
- 9. Шоколадка лежит в белой коробочке.Ответ№4:
- 10. Алеша, Боря и Витя учатся в одном
- 11. Алёша – на трамвае, Боря – на автобусе, Витя – на троллейбусеответ№5:
- 12. Из 9 монет одна – фальшивая, она тяжелее настояших. Найти ее за два взвешивания. Задача №6:
- 13. Одним взвешиванием можно уменьшить количество «подозрительных монет
- 14. Прямоугольник содержит 12 клеток. Найди пять
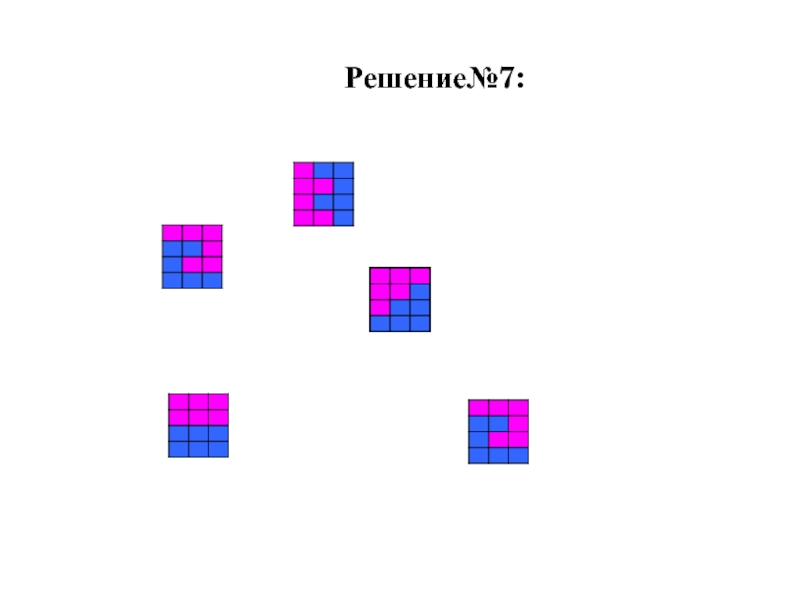
- 15. Решение№7:
- 16. На острове Контрастов живут и рыцари, и
- 17. Ясно, что если два человека сделали одно
- 18. 5 рыбаков съели 5 карпов за 5
- 19. 15 рыбаков съедят 15 карпов тоже за
- 20. Трое мальчиков имеют по некоторому количеству яблок.
- 21. Решение№10:
- 22. Над озерами летели гуси. На каждом озере
- 23. Посмотрим, сколько гусей село на последнем озере.
- 24. Летела стая гусей. На первое озеро села
- 25. х — всего гусей. На первое озеро
- 26. Скачать презентанцию
На дворе бегают куры и поросята. У всех вместе 20 голов и 52 ноги. Сколько всего кур и сколько поросят?Задача №1:
Слайды и текст этой презентации
Слайд 1Задачи на смекалку для 5-6 классов
Коньшина Елена Викторовна
Учитель математики
МАОУ
«Гимназия 8» г. Пермь
Слайд 2На дворе бегают куры и поросята. У всех вместе 20
голов и 52 ноги. Сколько всего кур и сколько поросят?
Задача
№1:
Слайд 4В клетке находтся фазаны и кролики. у всех животных 35
голов и 94 ноги. Сколько в клетке кроликов и фазанов?
Задача
№2:
Слайд 5И у фазанов и у кроликов по 1 голове, значит,
в клетке 35 животных.
х - фазанов
35-х - кроликов
у фазана 2
ноги, значит, 2х - всего ног у фазанову кролика 4 ноги, значит, 4(35-х) - всего ног у кроликов
т.к. всего 94 ноги, составляем уравнение
2х+4(35-х)=94
2х+140-4х=94
2х=46
х=23 - фазана
35-23=12 - кроликов
ответ: 23 фазана, 12 кроликов
Решение№2:
Слайд 6Беседуют трое: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: «Любопытно,
что один из нас русый, другой – брюнет, а третий
– рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос имеет каждый из беседующих?Задача №3:
Слайд 7Решение№3:
Беседуют трое: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: «Любопытно,
что один из нас русый, другой – брюнет, а третий
– рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос имеет каждый из беседующих?Решение:
Составим таблицу : отметим в ней каждое утверждение знаком «-»
Белокуров
Чернов
Рыжов
белокурый
брюнет
рыжий
-
-
-
-
+
-
+
-
+
Ответ: Белокуров - рыжий, Чернов - белокурый, Рыжов - брюнет
Слайд 8Имеется три коробочки: синяя, желтая и белая. В одной из
них лежит шоколадка, в другой – яблоко, а в третьей
ничего нет. Определите, в какой коробочке лежит шоколадка, если она лежит в одной этих двух коробочек желтой или белой. А ни в одной из белой синей коробочке нет яблока.Задача №4:
Слайд 10Алеша, Боря и Витя учатся в одном классе. Один ездит
домой из школы на автобусе, другой - на трамвае, третий
- на троллейбусе. Алеша однажды после уроков пошёл проводить друга до автобусной остановки. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «боря, ты дневник в школе оставил!» Кто на чем ездит домой?Задача №5:
Слайд 13Одним взвешиванием можно уменьшить количество «подозрительных монет втрое: нужно разделить
монеты на три одинаковые группы и сравнить две из них.
Если одна из групп легче, то фальшивая монета находится в ней, а если группы равны по весу, то фальшивая монета – в третьей группе.Решение№6:
Слайд 14 Прямоугольник содержит 12 клеток.
Найди пять способов разрезания прямоугольника
на две равные части так, чтобы линия разреза шла по
сторонам клеток.Задача №7:
Слайд 16На острове Контрастов живут и рыцари, и лжецы. Рыцари всегда
говорят правду, лжецы всегда лгут. Некоторые жители заявили, что на
острове чётное число рыцарей, а остальные заявили, что на острове нечётное число лжецов. Может ли число жителей острова быть нечётным?Задача №8:
Слайд 17Ясно, что если два человека сделали одно и то же
утверждение, то они либо оба лжецы, либо оба рыцари. Поскольку
на острове есть хотя бы один лжец и хотя бы один рыцарь, то либо все рыцари сделали первое утверждение, а все лжецы второе, либо наоборот. В первом случае и рыцарей, и лжецов чётное число, а во втором и тех, и других — нечётное число. Значит, число людей на острове обязательно чётно. Ответ: Нет, не может.Решение№8:
Слайд 185 рыбаков съели 5 карпов за 5 дней. Как вы
думаете, а за сколько дней 15 рыбаков съедят 15 карпов?
Задача 9:
Слайд 1915 рыбаков съедят 15 карпов тоже за 5 дней. Если
5 рыбаков съедают 5 карпов за определенный промежуток времени, то
у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов.Решение№9:
Слайд 20Трое мальчиков имеют по некоторому количеству яблок. Первый мальчик дает
другим столько яблок, сколько каждый из них имеет. Затем второй
мальчик дает двум другим столько яблок, сколько каждый из них теперь имеет; в свою очередь и третий дает каждому из двух других столько, сколько есть у каждого в этот момент. После этого у каждого из мальчиков оказывается по 8 яблок.Сколько яблок было у каждого мальчика в начале?
Задача №10:
Слайд 22Над озерами летели гуси. На каждом озере садилась половина гусей
и еще полгуся, остальные летели дальше. Все сели на семи
озерах.Задача №11:
Слайд 23Посмотрим, сколько гусей село на последнем озере. Так как дальше
никто не полетел, то все гуси, пролетающие над седьмым озером,
сели на нём. А это означает, что половина всех этих гусей, да ещё полгуся - это и есть все эти гуси. То есть половина этих гусей - это ровно полгуся. То есть на последнем озере сел ровно 1 гусь. Далее, на шестом озере село 2 гуся - если дальше полетел 1 гусь, а села половина гусей и еще полгуся, то всего летело 3 гуся. Несложно убедиться, что на пятом озере село 4 гуся, на четвёртом - 8, на третьем - 16, на втором - 32, а на первом - 64. Таким образом всего на озёра село 1+2+4+8+16+32+64=127 гусей. А так как все гуси сели на семи озёрах, то и изначально летело 127 гусей.Решение№11:
Слайд 24Летела стая гусей. На первое озеро села половина всех гусей
и ещё пол гуся, на второе - половина всех остальных
гусей и ещё пол гуся, на третье — половина оставшихся гусей и ещё полгуся, на четвёртое — половина оставшихся и ещё полгуся, и наконец на пятое — половина остальных и полгуся. После этого все гуси оказались на 5 озёрах. Сколько было гусей в стае?Задача №12:
Слайд 25
х — всего гусей.
На первое озеро село 1/2х+1/2.
На второе: 1/2(х-(1/2х+1/2))+1/2=1/4х+1/4.
На третье:
...=1/8х+1/8.
На четвёртое: ...=1/16х+1/16.
На пятое: ...=1/32х+1/32.
1/2х+1/2+1/4х+1/4+1/8х+1/8+1/16х+1/16+1/32х+1/32=х
31x+31=32x
х=31
Решение№11:
