Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
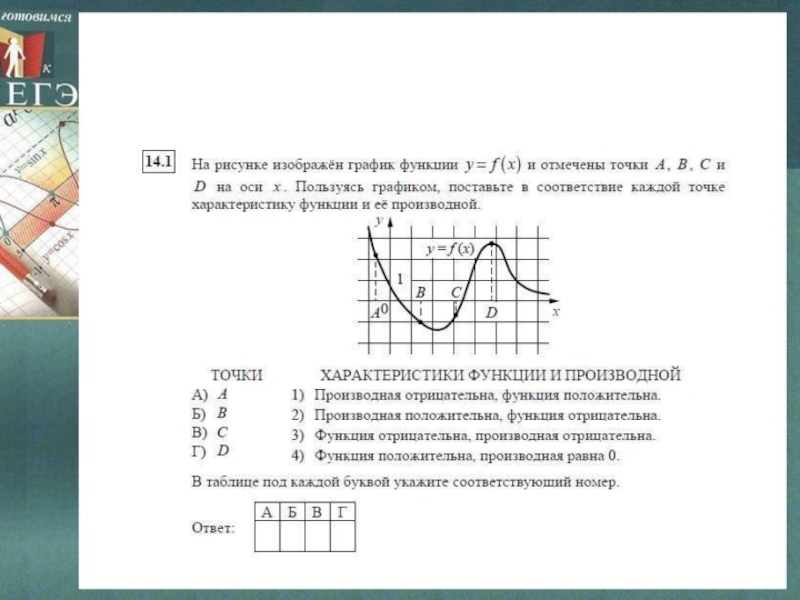
Задание 7 ЕГЭ по математике
Содержание
- 1. Задание 7 ЕГЭ по математике
- 2. Слайд 2
- 3. Слайд 3
- 4. В данной подборке заданий рассматриваются типы
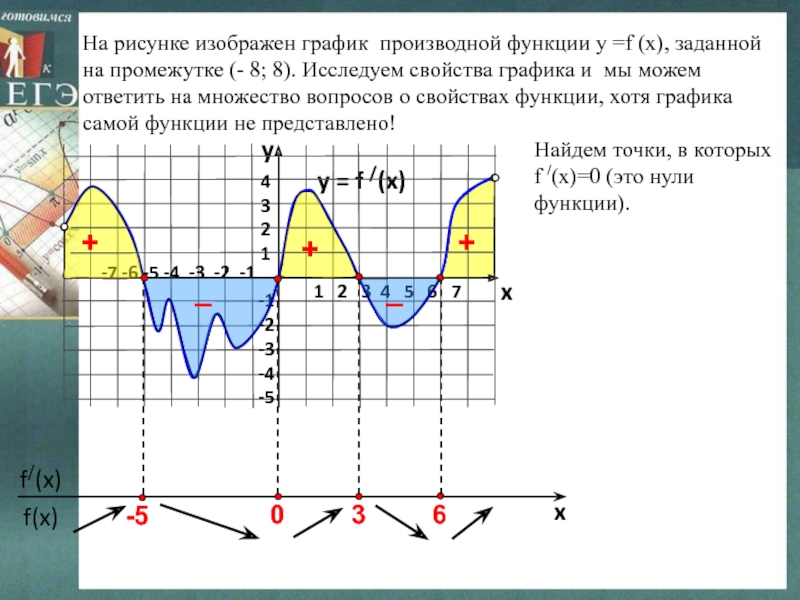
- 5. На рисунке изображен график производной функции у
- 6. По этой схеме мы можем дать ответы
- 7. Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите точку экстремума функции
- 8. Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите промежутки возрастания функции
- 9. Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите промежутки возрастания функции
- 10. Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите промежутки убывания функции
- 11. Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка
- 12. Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка
- 13. На рисунке изображен график функции y =
- 14. На рисунке изображен график функции y =
- 15. На рисунке изображен график функции y =
- 16. На рисунке изображен график функции y =
- 17. На рисунке изображен график функции y =
- 18. Слайд 18
- 19. На рисунке изображен график функции y =
- 20. На рисунке изображен график функции y =
- 21. На рисунке изображен график функции y =
- 22. Производная функции в точке х0 равна 0
- 23. На рисунке изображен график функции y =
- 24. На рисунке изображен график производной функции f(x),
- 25. Адреса сайтов в сети Интернетwww.fipi.ru –
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 17
Математика
Вабищевич Светлана Николаевна
Преподаватель ФГКОУ НСВУ МВД России
г.Новочеркасск Ростовской обл.
Задание
Мастер
– класс
Слайд 4В данной подборке заданий рассматриваются
типы задач:
Нахождение точек максимума и
минимума по графику производной функции.
Нахождение длины промежутков возрастания или убывания
функции, точек максимума и минимума по графику функции.Нахождение значения производной в заданной точке, если задан график функции и касательная к нему.
Определение количества целых точек, в которых производная функции отрицательна, положительна.
Нахождение количества точек, в которых производная функции у = f (x) равна 0.
Слайд 5На рисунке изображен график производной функции у =f (x), заданной
на промежутке (- 8; 8). Исследуем свойства графика и мы
можем ответить на множество вопросов о свойствах функции, хотя графика самой функции не представлено!y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
Найдем точки, в которых f /(x)=0 (это нули функции).
+
–
–
+
+
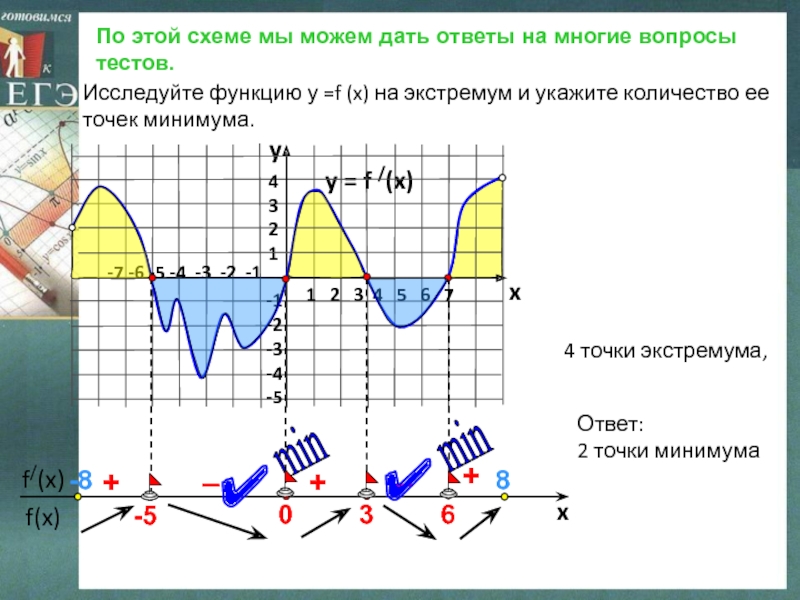
Слайд 6По этой схеме мы можем дать ответы на многие вопросы
тестов.
y = f /(x)
1 2 3 4
5 6 7-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
4 точки экстремума,
Ответ:
2 точки минимума
-8
8
Слайд 7Пример
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
Найдите точку экстремума функции у =f (x)
на отрезке [– 6; –1]
Ответ: xmax = – 5
1
2 3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
-8
8
Слайд 8Пример
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
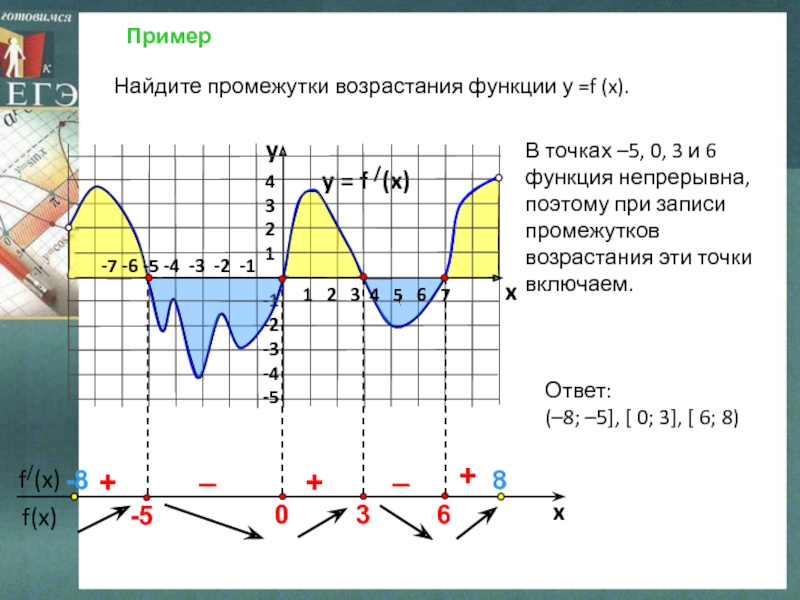
Найдите промежутки возрастания функции у =f (x).
В
точках –5, 0, 3 и 6
функция непрерывна, поэтому при
записи промежутков возрастания эти точки включаем.1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
Ответ:
(–8; –5], [ 0; 3], [ 6; 8)
-8
8
Слайд 9Пример
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
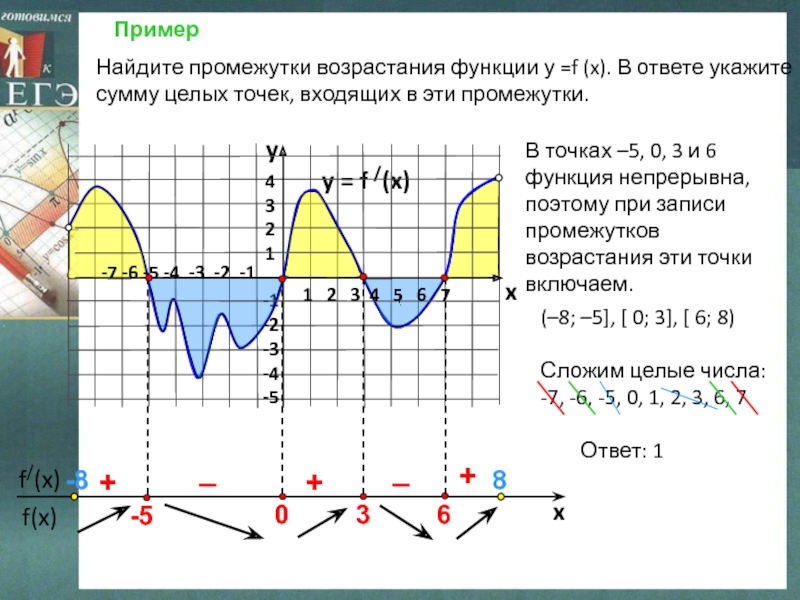
Найдите промежутки возрастания функции у =f (x).
В ответе укажите сумму целых точек, входящих в эти промежутки.
В точках –5, 0, 3 и 6
функция непрерывна, поэтому при записи промежутков возрастания эти точки включаем.
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
Сложим целые числа:
-7, -6, -5, 0, 1, 2, 3, 6, 7
-8
8
(–8; –5], [ 0; 3], [ 6; 8)
Ответ: 1
Слайд 10Пример
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
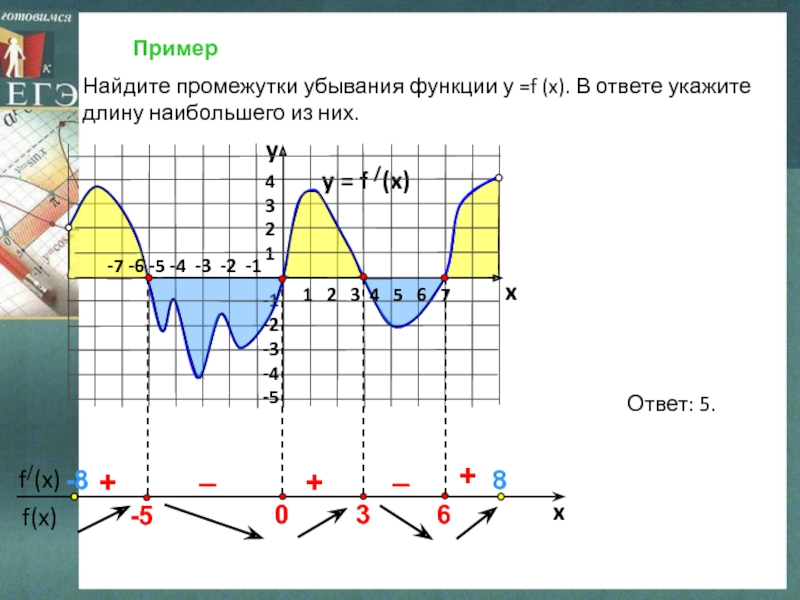
Найдите промежутки убывания функции у =f (x).
В ответе укажите длину наибольшего из них.
1 2
3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
Ответ: 5.
-8
8
Слайд 11Пример
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
В какой точке отрезка [– 4; –1]
функции у =f (x) принимает наибольшее значение?
1 2
3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
Ответ: – 4.
-8
8
На отрезке [– 4; –1] функция у =f (x) убывает, значит, наибольшее значение на данном отрезке функция будет принимать в точке – 4.
Слайд 12Пример
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
В какой точке отрезка [– 4; –1]
функции у =f (x) принимает наименьшее значение?
1 2
3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
Ответ: – 1.
-8
8
На отрезке [– 4; –1] функция у =f (x) убывает, значит, наименьшее значение на данном отрезке функция будет принимать в конце отрезка точке х= – 1.
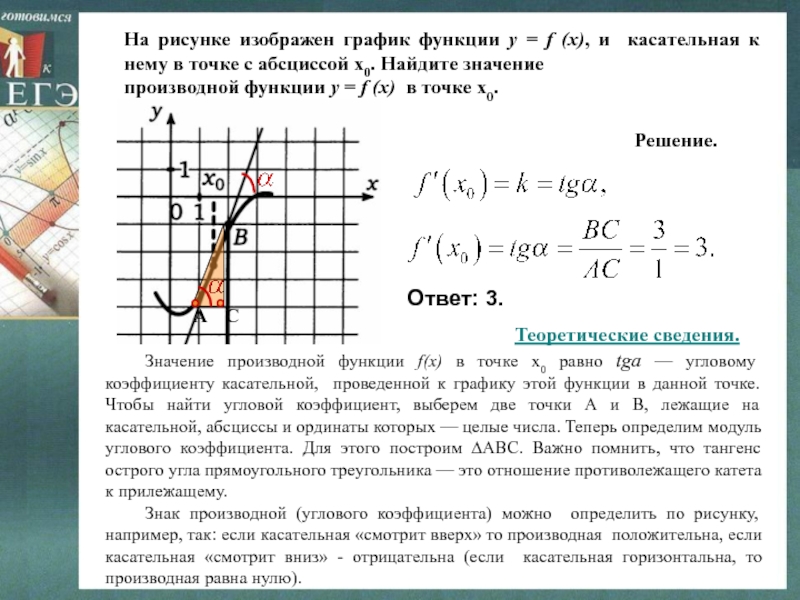
Слайд 13На рисунке изображен график функции y = f (x), и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции y = f (x) в точке х0.
Значение производной функции f(x) в точке х0 равно tga — угловому коэффициенту касательной, проведенной к графику этой функции в данной точке. Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых — целые числа. Теперь определим модуль углового коэффициента. Для этого построим ∆ABC. Важно помнить, что тангенс острого угла прямоугольного треугольника — это отношение противолежащего катета к прилежащему.
Знак производной (углового коэффициента) можно определить по рисунку, например, так: если касательная «смотрит вверх» то производная положительна, если касательная «смотрит вниз» - отрицательна (если касательная горизонтальна, то производная равна нулю).
Решение.
Ответ: 3.
Теоретические сведения.
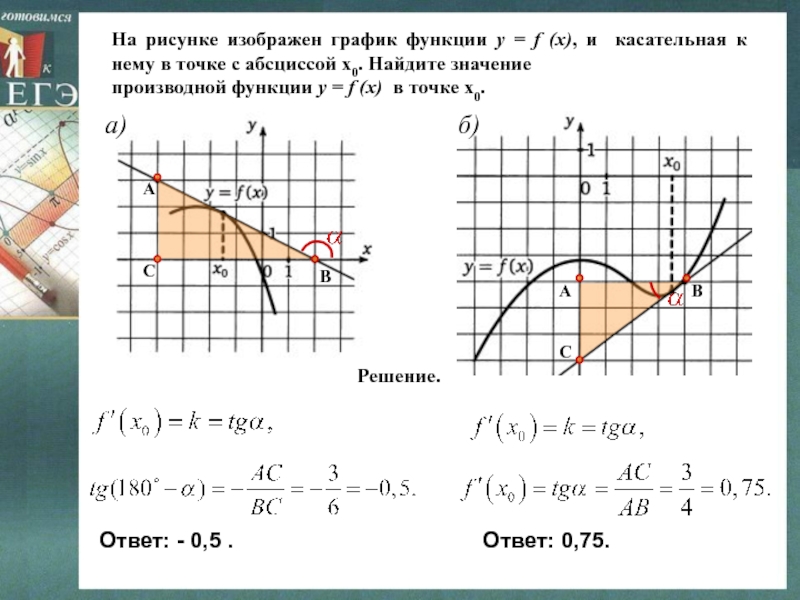
Слайд 14На рисунке изображен график функции y = f (x), и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции y = f (x) в точке х0.
Решение.
Ответ: - 0,5 .
Ответ: 0,75.
С
В
А
a)
б)
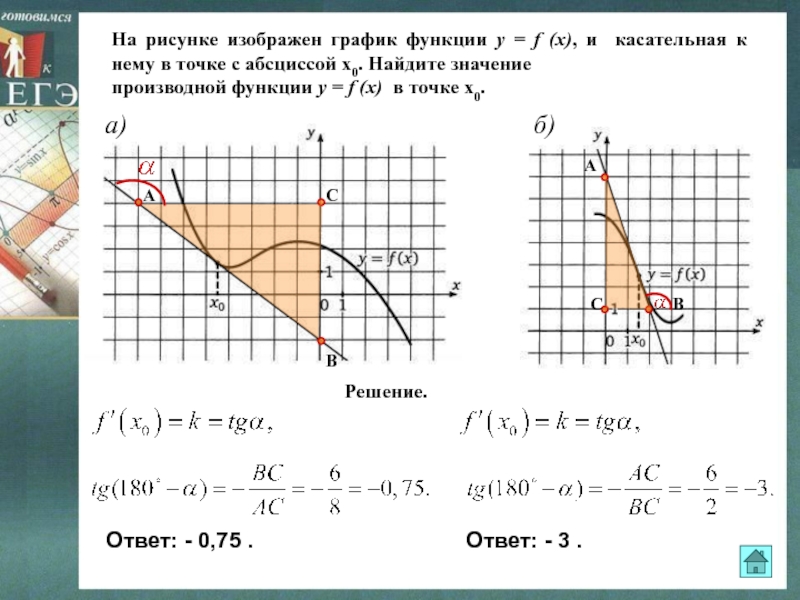
Слайд 15На рисунке изображен график функции y = f (x), и
касательная к нему в точке с абсциссой х0. Найдите значение
производной функции y = f (x) в точке х0.
Решение.
Ответ: - 0,75 .
А
В
С
А
В
С
Ответ: - 3 .
a)
б)
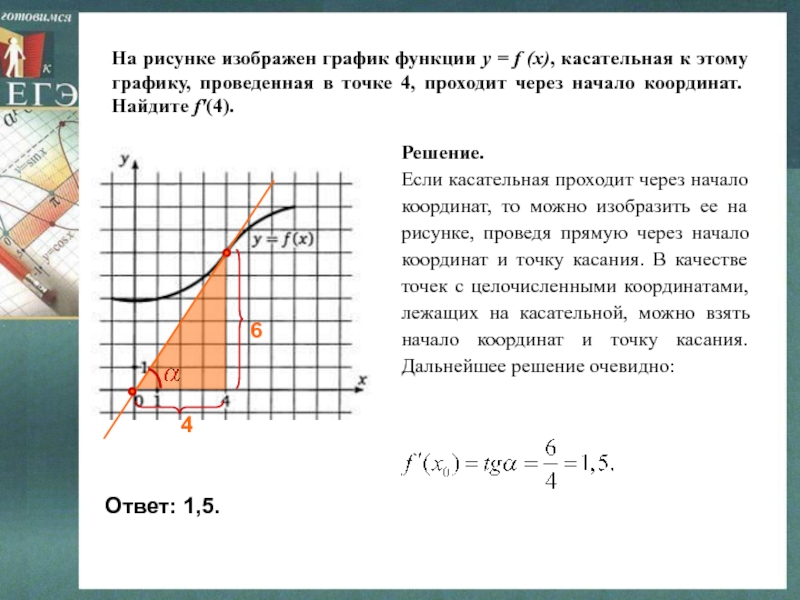
Слайд 16На рисунке изображен график функции y = f (x), касательная
к этому графику, проведенная в точке 4, проходит через начало
координат. Найдите f'(4).Решение.
Если касательная проходит через начало координат, то можно изобразить ее на рисунке, проведя прямую через начало координат и точку касания. В качестве точек с целочисленными координатами, лежащих на касательной, можно взять начало координат и точку касания. Дальнейшее решение очевидно:
Ответ: 1,5.
6
4
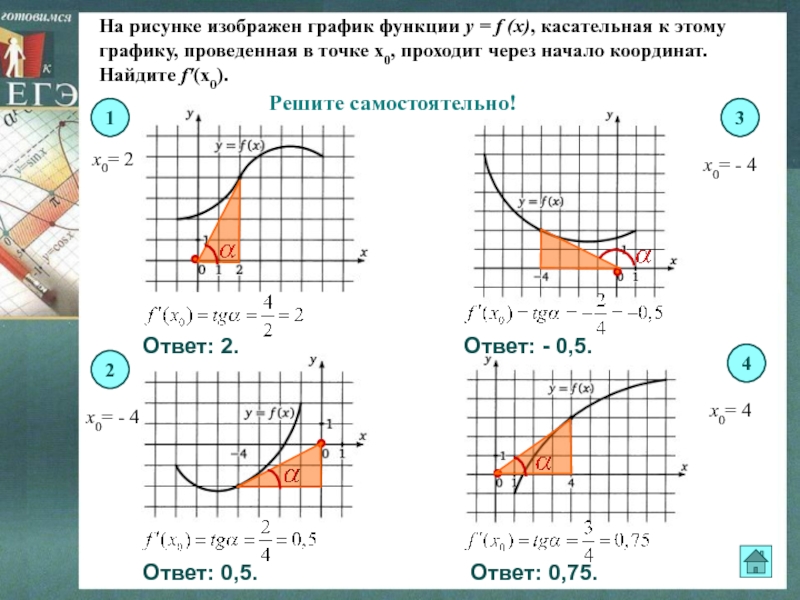
Слайд 17На рисунке изображен график функции y = f (x), касательная
к этому графику, проведенная в точке х0, проходит через начало
координат. Найдите f'(х0).х0= 2
х0= - 4
х0= - 4
х0= 4
1
3
4
2
Решите самостоятельно!
Ответ: 2.
Ответ: 0,5.
Ответ: - 0,5.
Ответ: 0,75.
Слайд 18
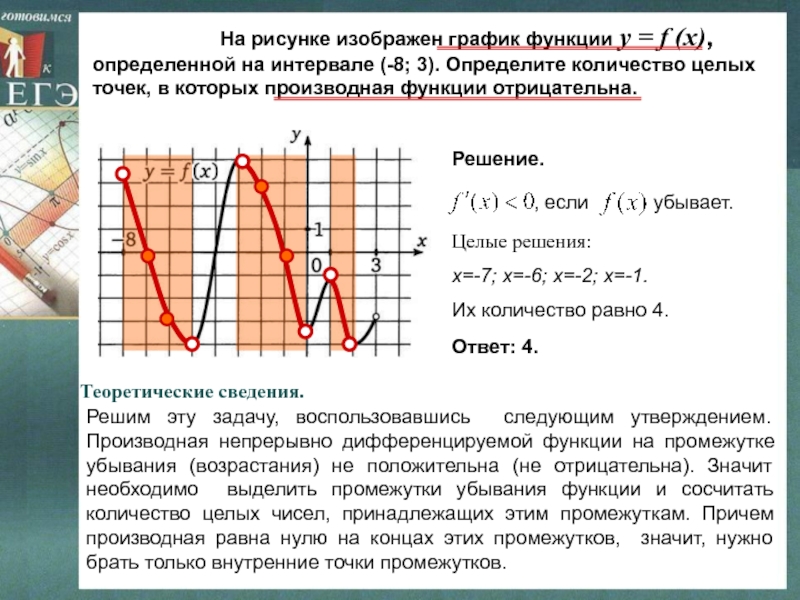
На рисунке изображен график функции y = f
(x),определенной на интервале (-8; 3). Определите количество целых точек, в которых производная функции отрицательна.
Решим эту задачу, воспользовавшись следующим утверждением. Производная непрерывно дифференцируемой функции на промежутке убывания (возрастания) не положительна (не отрицательна). Значит необходимо выделить промежутки убывания функции и сосчитать количество целых чисел, принадлежащих этим промежуткам. Причем производная равна нулю на концах этих промежутков, значит, нужно брать только внутренние точки промежутков.
Решение.
Целые решения:
х=-7; х=-6; х=-2; х=-1.
Их количество равно 4.
Ответ: 4.
Теоретические сведения.
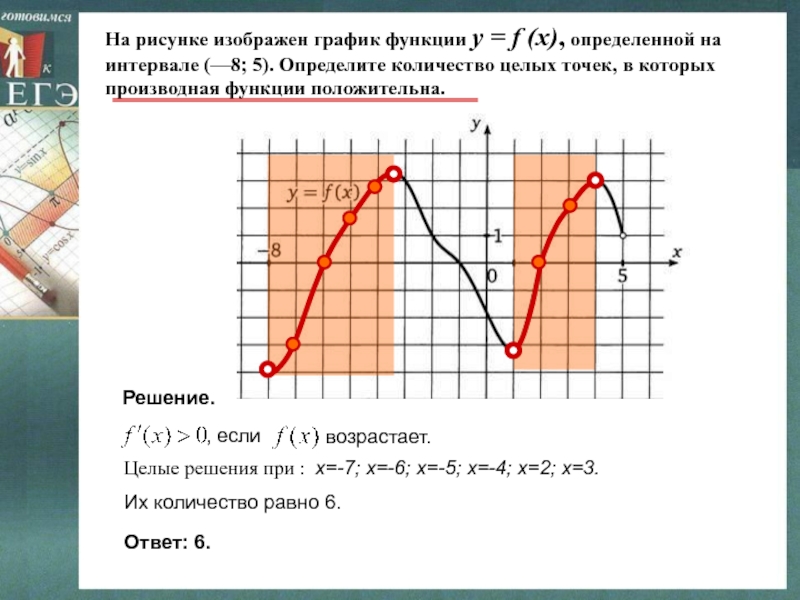
Слайд 19На рисунке изображен график функции y = f (x), определенной
на интервале (—8; 5). Определите количество целых точек, в которых
производная функции положительна.Решение.
Целые решения при : х=-7; х=-6; х=-5; х=-4; х=2; х=3.
Их количество равно 6.
Ответ: 6.
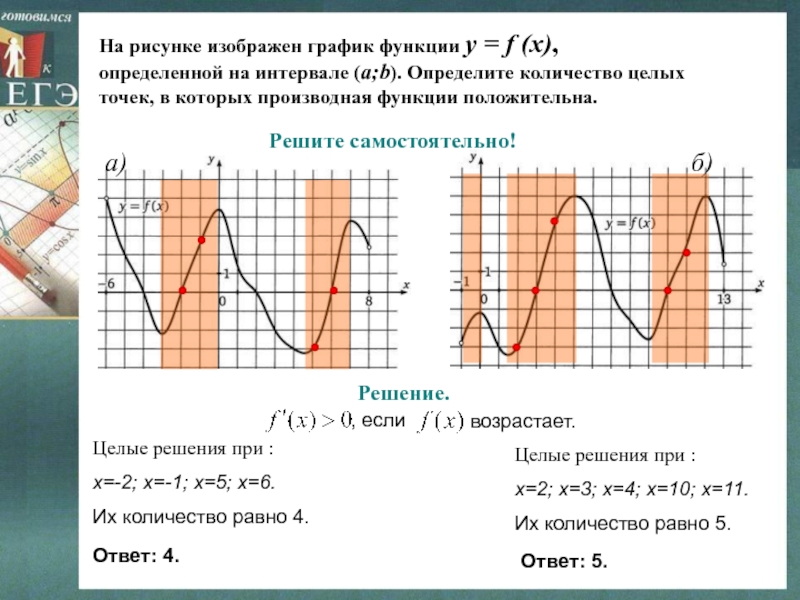
Слайд 20На рисунке изображен график функции y = f (x),
определенной на интервале (a;b). Определите количество целых
точек, в которых
производная функции положительна. a)
б)
Решите самостоятельно!
Решение.
Целые решения при :
х=-2; х=-1; х=5; х=6.
Их количество равно 4.
Целые решения при :
х=2; х=3; х=4; х=10; х=11.
Их количество равно 5.
Ответ: 4.
Ответ: 5.
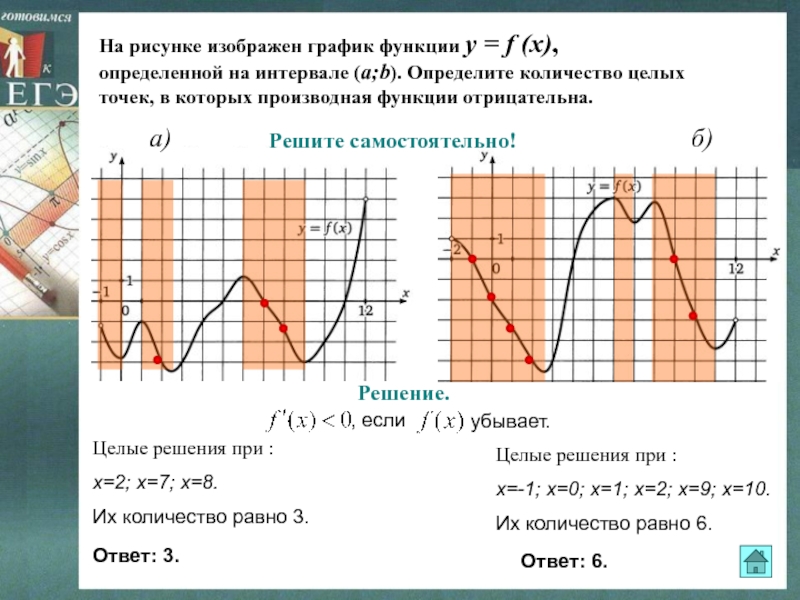
Слайд 21На рисунке изображен график функции y = f (x),
определенной на интервале (a;b). Определите количество целых
точек, в которых
производная функции отрицательна. Решите самостоятельно!
a)
б)
Решение.
Целые решения при :
х=2; х=7; х=8.
Их количество равно 3.
Целые решения при :
х=-1; х=0; х=1; х=2; х=9; х=10.
Их количество равно 6.
Ответ: 3.
Ответ: 6.
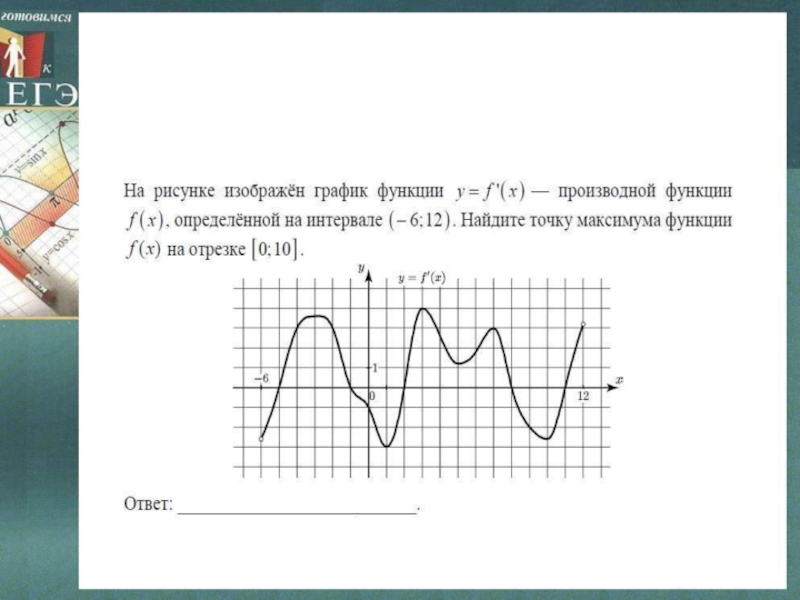
Слайд 22Производная функции в точке х0 равна 0 тогда и только
тогда, когда касательная к графику функции, проведенная в точке с
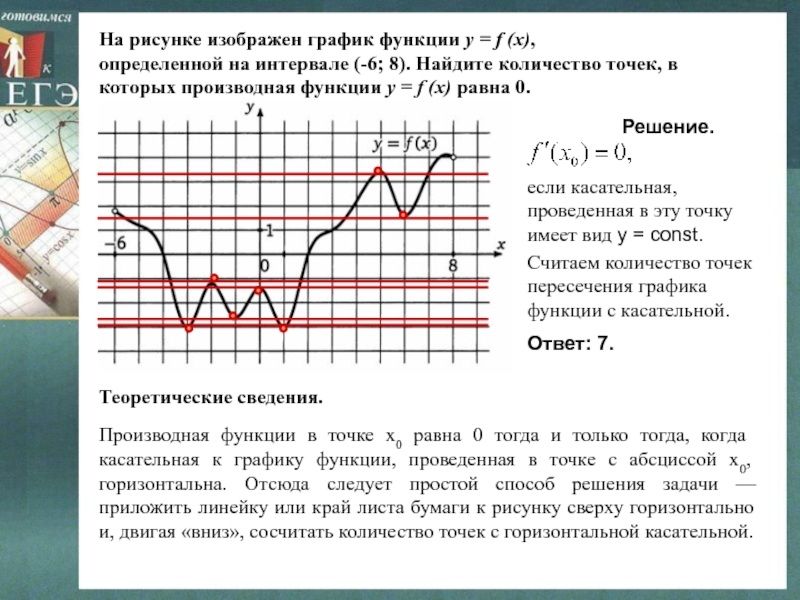
абсциссой х0, горизонтальна. Отсюда следует простой способ решения задачи — приложить линейку или край листа бумаги к рисунку сверху горизонтально и, двигая «вниз», сосчитать количество точек с горизонтальной касательной.На рисунке изображен график функции y = f (x),
определенной на интервале (-6; 8). Найдите количество точек, в
которых производная функции y = f (x) равна 0.
Теоретические сведения.
Решение.
если касательная, проведенная в эту точку имеет вид у = const.
Считаем количество точек пересечения графика функции с касательной.
Ответ: 7.
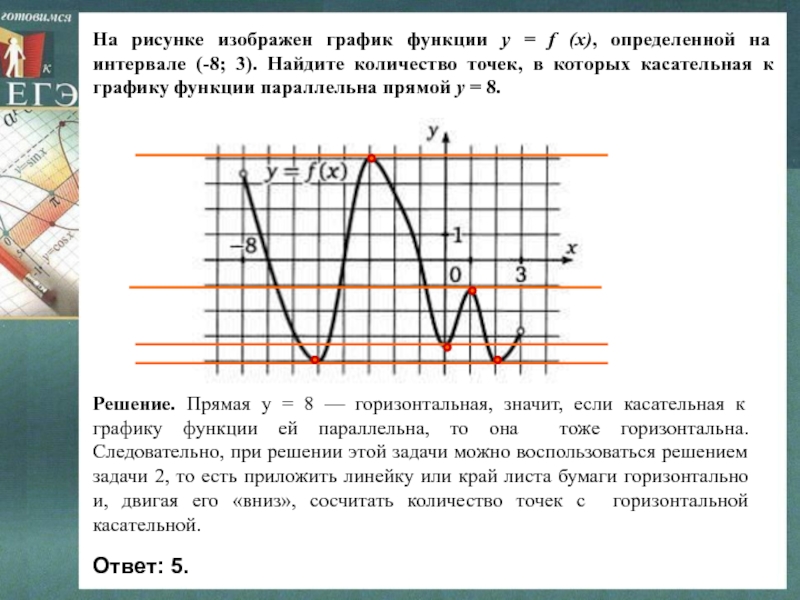
Слайд 23На рисунке изображен график функции y = f (x), определенной
на интервале (-8; 3). Найдите количество точек, в которых касательная
к графику функции параллельна прямой у = 8.Решение. Прямая у = 8 — горизонтальная, значит, если касательная к графику функции ей параллельна, то она тоже горизонтальна. Следовательно, при решении этой задачи можно воспользоваться решением задачи 2, то есть приложить линейку или край листа бумаги горизонтально и, двигая его «вниз», сосчитать количество точек с горизонтальной касательной.
Ответ: 5.
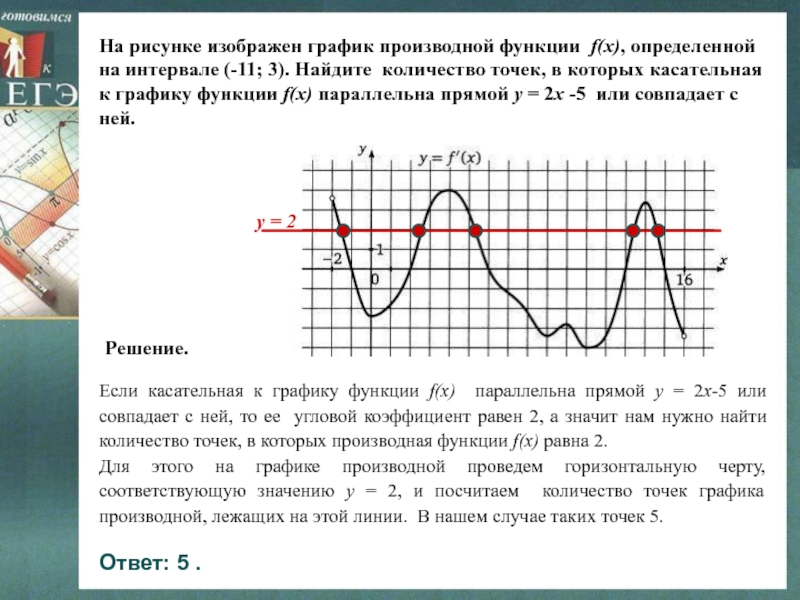
Слайд 24На рисунке изображен график производной функции f(x), определенной на интервале
(-11; 3). Найдите количество точек, в которых касательная к графику
функции f(x) параллельна прямой y = 2x -5 или совпадает с ней.Если касательная к графику функции f(x) параллельна прямой y = 2x-5 или совпадает с ней, то ее угловой коэффициент равен 2, а значит нам нужно найти количество точек, в которых производная функции f(x) равна 2.
Для этого на графике производной проведем горизонтальную черту, соответствующую значению y = 2, и посчитаем количество точек графика производной, лежащих на этой линии. В нашем случае таких точек 5.
Решение.
y = 2
Ответ: 5 .
Слайд 25 Адреса сайтов в сети Интернет
www.fipi.ru – Федеральный институт педагогических
измерений (ФИПИ). Особенно обратите внимание на раздел «Открытый сегмент ФБТЗ»
– это система для подготовки к ЕГЭ - в режиме on-line. Вы можете отвечать на вопросы банка заданий ЕГЭ по различным предметам, а так же по выбранной теме.http://mathege.ru -Открытый банк задач ЕГЭ по математике. Главная задача открытого банка заданий ЕГЭ по математике — дать представление о том, какие задания будут в вариантах Единого государственного экзамена по математике в 2010 году, и помочь выпускникам сориентироваться при подготовке к экзамену. Здесь же можно найти все пробные ЕГЭ по математике, которые уже прошли.
http://egetrener.ru/ - математика: видеоуроки, решение задач ЕГЭ.
http://ege-trener.ru/ - очень увлекательная и эффективная подготовка к ЕГЭ по математике. Зарегистрируйтесь и попытайтесь попасть в 30-ку лучших!
uztest.ru — бесплатные материалы для подготовки к ЕГЭ (и не только к ЕГЭ) по математике: интерактивные тематические тренажеры, возможность записи на бесплатные on-line курсы по подготовке к ЕГЭ.
www.ege.edu.ru – официальный информационный портал единого государственного экзамена.
On-line видеолекции "Консультации по ЕГЭ" по всем предметам.
Ролики категории ЕГЭ. Лекции по математике
http://www.alexlarin.narod.ru/ege.html - материалы для подготовки к ЕГЭ по математике (сайт Ларина Александра Александровича).
http://www.diary.ru/~eek/ - сообщество, оказывающее помощь в решении задач по математике, здесь же можно скачать много полезных книг по математике, в том числе для подготовки к ЕГЭ.
http://4ege.ru/ - ЕГЭ портал, всё последнее к ЕГЭ. Вся информация о егэ. ЕГЭ 2013.


![Задание 7 ЕГЭ по математике Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите точку экстремума функции у =f (x) на Примерy = f /(x) 4321-1-2-3-4-5yx+––++Найдите точку экстремума функции у =f (x) на отрезке [– 6; –1]Ответ: xmax =](/img/tmb/5/415071/4f55318d354ad38a14f01f08e1c91616-800x.jpg)
![Задание 7 ЕГЭ по математике Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции у =f (x) принимает наибольшее значение?](/img/tmb/5/415071/57a664ad191c0a7f9c84219eeade41ce-800x.jpg)
![Задание 7 ЕГЭ по математике Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции у =f (x) принимает наименьшее значение?](/img/thumbs/c0bea97bb12a6fa5d64d4e2e021b143b-800x.jpg)