Задания типа 18

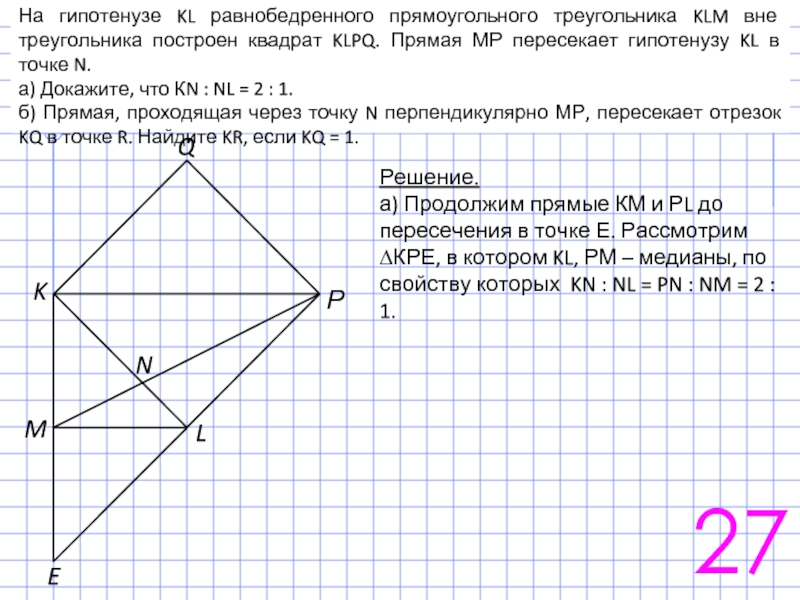
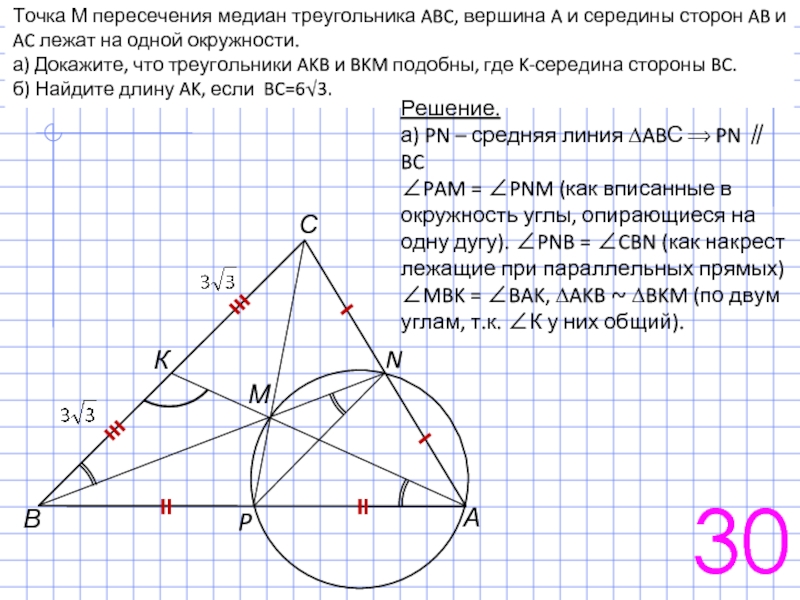
и их линии центров. а) Докажите, что периметр треугольника с вершинами

Решение.
a) Найдем периметр ∆О1О2О3



(т.е. диаметру большей окружности)

1

образом. Третья окружность касается первых двух и их линии центров. а)

1

неё на все стороны параллелограмма (или их продолжения) опустили перпендикуляры.
а)

Решение.
a) ∆AOQ ~ ∆CON (по двум углам) ⟹
AO : CO = OQ : ON
∆AOM ~ ∆COP (по двум углам) ⟹
AO : CO = OM : OP
⟹ OQ : ON = OM : OP ⟹
∆QOM ~ ∆NOP (по углу ∠MOQ = ∠PON = = 120° и двум прилежащим сторонам) ⟹ ∠OQM = ∠ONP (накрест лежащие) ⟹PN ∥ QM.

б)

⟹

продолжении отрезка AO за точку O отмечена точка K так,

Решение.
a) Пусть ∠АВС = х; ∠ВOС = 2∠АВС = 2х (как центральный и вписанный углы с общей дугой ВС); ∠АКС = ∠ОКС = 90° − х
∆ВOС – р/б; ОВ = ОС (радиусы) ⟹
∠ОВС = ∠ОСВ = (180° – 2х) : 2 = 90° − х
⟹ ∠ОКС = ∠ОВС (вписанные в окружность с общей дугой ОС)
ОВКС – вписанный четырёхугольник.

б)

По теореме синусов:

3

BC в точке P и пересекает отрезок BO в точке

Решение.

4

BC в точке P и пересекает отрезок BO в точке

Решение (продолжение).

4

E. В треугольник ADE вписана окружность, касающаяся стороны AE в

Решение.
a) ∠АDE = ∠СDE = ∠АED (как накрест лежащие при параллельных прямых
AB и DC и секущей DE)
∆AOT = ∆AOK (по общей гипотенузе и катетам ОТ = ОК = r) ⟹ AT = AK ⟹
∆ATK – р/б ⟹ ∠ATK = ∠AKT
∆AKT ~ ∆AED (по общему углу А и двум прилежащим сторонам) ⟹ ∠ATK =
= ∠ADE – соответственные ⟹ KT ∥ DE

б) ∆ADE – р/б; AD = AE = 6, АР – высота и медиана ⟹ DP = EP. Пусть АТ = АК = х, тогда TD = PD = 6 – x, т. к. ∆AKT ~ ∆AED ⟹ AT : AD = KT : ED, x : 6 = 3 : 2(6 – x) ⟹ x = 3.
Значит, ∆AKT и ∆AED – равносторонние, ∠BAD = 60°.

Ответ: 60.

5

в точке D, причём AD = R.
а) Докажите, что треугольник

Решение.
a) т.к. AD = R и OD⊥AD (как радиус окр., проведенный в точку касания) ⟹ ADOE – квадрат ⟹ ∠САВ = 90° ⟹ ∆AВС – п/у

б) АС = AD + CD = 20; CD = CF = 15 (по свойству вписанной окружности в ∆ABС)
Пусть ВЕ = BF = х, тогда по т. Пифагора
(5 + х)2 + 202 = (15 + х)2 ⟹ х = 10.
В п/у АВС sin∠B = АС : ВС = 20/25 = 0,8
S∆BEF = ½ BE ∙ BF sin∠B = ½ ∙ 102 ∙ 0,8 = 40.

Ответ: 40.

6

и 9. Найдите радиус третьей окружности, которая касается двух данных

Решение. (1 случай)
АО3 ⊥ О1О2 (как радиус окружности, проведенный в точку касания) ⟹ ∆АО1О3 и ∆АО3О2 – п/у.
Пусть AO3 = R и АО1 = х, тогда АО2 = 21 – х. Применив т. Пифагора, составим систему уравнений:

Ответ: 8.

7

и 9. Найдите радиус третьей окружности, которая касается двух данных

Решение. (2 случай)
АО3 ⊥ О1О2 (как радиус окружности, проведенный в точку касания) ⟹ ∆АО1О3 и ∆АО3О2 – п/у.
Пусть AO3 = R и АО1 = х, тогда АО2 = 21 + х. Применив т. Пифагора, составим систему уравнений:

Ответ: 80.

A точка пересечения окружностей, построенных на сторонах AB и AC

Решение. (1 случай)
Т.к. точки A, С и D лежат на окружности с центром О2 и АС – диаметр, то ∆ADC – п/у; аналогично, ∆ADВ – п/у ⟹ D лежит на ВС.

Пусть BD = x, в п/у ∆ADC выразим АС = 2AD через х:



В п/у ∆AВD по т. Пифагора:

По т. косинусов в ∆АВС:

8

A точка пересечения окружностей, построенных на сторонах AB и AC

Решение. (2 случай)
Т.к. точки A, С и D лежат на окружности с центром О2 и АС – диаметр, то ∆ADC – п/у; аналогично, ∆ADВ – п/у ⟹ D лежит на ВС.

В п/у ∆ADC выразим АС = 2AD через х:



В п/у ∆AВD по т. Пифагора:

По т. косинусов в ∆АВС:

8

PD = CD = 12, CQ = 4. Найдите CP

Решение. (1 случай)
в ∆PQC по т. косинусов:



в ∆PDC по т. косинусов:



(по свойству четырехугольника, вписанного в окружность).
Приравнивая эти выражения, получим уравнение относительно cos∠PQC:

Подставив обратно в любое из выражений, найдем PC:

9

PD = CD = 12, CQ = 4. Найдите CP

Решение. (2 случай)
в ∆PQC по т. косинусов:



в ∆PDC по т. косинусов:



(по свойству вписанных углов в окружность).
Приравнивая эти выражения, получим уравнение относительно cos∠PQC

Подставив обратно в любое из выражений, найдем PC:

9

соответственно касаются внешним образом в точке C. AO1 и BO2

Решение. (1 случай)
Т.к. ∠АО1C = 60° и АО1 ∥ ВО2, то по ∠ВО2C = 120° (как внутренние односторонние при параллельных прямых и секущей О1О2)
В р/с ∆АО1С АС = 1;
в р/б ∆ВО2С найдем по т. косинусов:



∠АCВ = 180° - 60° - 30° = 90° ⟹
в п/у ∆АВC по т. Пифагора:

Ответ: 7.

10

соответственно касаются внешним образом в точке C. AO1 и BO2

Решение. (2 случай)
Т.к. ∠АО1C = 60° и АО1 ∥ ВО2, то по ∠ВО2C = 60° (как накрест лежащие при параллельных прямых и секущей О1О2)
∠ВCО2 = ∠АCО1 = 60° (как вертикальные) ⟹ ∆ВО2С – р/с ⟹
ВС = 4; в р/с ∆АО1С АС = 1;
АВ = ВС + АС = 1 + 4 = 5

Ответ: 5.

10

то ∠ВАО1 = 15° = ∠CАО2 (как вертикальные) ⟹ ∠АСО2

Окружности радиусов 3 и 5 с центрами O1 и O2 соответственно касаются в точке A. Прямая, проходящая через точку A, вторично пересекает меньшую окружность в точке B, а большую – в точке C . Найдите площадь треугольника BCO2, если ∠ABO1= 15°.

11

соответственно касаются в точке A. Прямая, проходящая через точку A,

Решение. (2 случай)
Т.к. ∠АВО1 = 15° и ∆АО1В – р/б,
то ∠ВАО1 = ∠АCО2 = 15° (как углы р/б ∆АО2С ) ⟹
∠ВО1А = ∠CО2А = 180° − 2 ∙ 15°= 150°

⟹

также вписана в этот угол и пересекается с первой в

Решение. (1 случай)
О1А ⊥ АС и О2В ⊥ АС (как радиусы окружностей, проведенных в точку касания) ⟹ ∆АСО1 и ∆ВСО2 – п/у с углом ∠С = 30° ⟹ СО1 = 12, СО2 = СО1 – О1О2 = 8.
Значит, ВО2 = 4 = О1О2 ⟹ О1 лежит на второй окружности.
∆NO1О2 – р/б, т.к. NO2 = O1О2 = 4 (радиусы) NO1 = 6, тогда по формуле Герона:

12

также вписана в этот угол и пересекается с первой в

Решение. (2 случай)
О2А ⊥ АС и О1В ⊥ АС (как радиусы окружностей, проведенных в точку касания) ⟹ ∆АСО2 и ∆ВСО1 – п/у с углом ∠С = 30° ⟹ СО1 = 12, СО2 = СО1 + О1О2 = 16.
АO2 = NО2 = 8 (радиусы) NO1 = 6, тогда по формуле Герона:

12

ними равен 2/5. В треугольник вписан ромб, имеющий с треугольником

14

Решение. (1 случай)
Пусть АВ = 8, АС = 10, примем АМ = АР = х, тогда ВМ = 8 – х; СР = 10 – х;
∆AВС ~ ∆МВК (по двум углам) ⟹
МК : АС = ВМ : АВ
х : 10 = (8 – х) : 8 ⟹ х = 40/9.

Ответ: 40/9.

ними равен 2/5. В треугольник вписан ромб, имеющий с треугольником

14

Ответ: 5.

угла равны 4 и 3. Через точку M проведена прямая,

Решение.
Пусть ВК = х, АР = у, тогда АС = 4 + у; СВ = 3 + х.
∆ВКМ ~ ∆МРА (по двум углам) ⟹ ВК : МР = КМ : РА, х : 3 = 4 : у ⟹ ху = 12.

Получим систему:

⟹

По т. Пифагора в п/у ∆АВС:

15

средней линии, параллельной стороне BC. Известно, что BC = 11.

Решение.
Пусть АВ = х, АС = у, тогда Р∆АВС = АВ + АС + ВС = х + у + 11;
MN = 5,5 (как средняя линия ∆АВС).
MNCB – трапеция, в которую вписана окружность ⟹
MN + BC = MB + CN = ½ (x + y) = 5,5 + 11 = 16,5 ⟹ х + у = 33;

P ∆АВС = 33 + 11 = 44.
По формуле Герона:

Получим систему:

Ответ: 13 или 20.

16

продолжений двух других его сторон. Радиусы двух вневписанных окружностей прямоугольного

Решение. (1 случай)
Пусть обе окружности касаются катетов и продолжений двух других сторон, тогда О1О2 = О1С + СО2 (где О1С и СО2 – диагонали квадратов, построенных на радиусах окружностей в соответствии со свойством радиуса окружности, проведенного в точку касания)

17

продолжений двух других его сторон. Радиусы двух вневписанных окружностей прямоугольного

17

Решение. (2 случай)
Пусть одна из окружностей касается гипотенузы, а другая одного из катетов и продолжений двух других сторон, тогда в п/у
∆МО1О2 по т. Пифагора

(где О2М = О2К + КМ = 17 + 7 = 24 – сумма радиусов;
О1М = МН – О1Н = 17 – 7 = 10 – разность радиусов)

Ответ: 26.

8. Прямая, проходящая через вершину M , касается окружности с

Решение. (1 случай)
∆MNQ ~ ∆КHQ (по двум углам) ⟹ МN : KH = NQ : HQ. Пусть KQ = x, тогда QN = 11 – x, в п/у ∆KHQ

Ответ: 5.

18

8. Прямая, проходящая через вершину M, касается окружности с центром

Решение. (2 случай)
∆MNQ ~ ∆КHQ (по двум углам) ⟹ МN : KH = NQ : HQ. Пусть KQ = x, тогда
QN = 11 + x, в п/у ∆KHQ

18

26 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия

19

Решение. (1 случай)
BC = 24, EF = 12, значит СЕ = BF = (24 – 12) : 2 = 6 (как средние линии ∆KLM и ∆NLM) ⟹ LM = 12;
KN = 2(CE + EF) = 2(6 + 12) = 36 (CF – средняя линия ∆KLN)
∆AKN ~ ∆ALM (по двум углам) ⟹ AL : AK = LM : KN = AM : AN.

Пусть AL = x, AM = y, тогда AK = 10 + x,
AN = 26 + y.
x : (10 + x) = 12 : 36 ⟹ x = 5;
y : (26 + y) = 12 : 36 ⟹ y = 13.
Значит, ∆AKN ~ ∆ALM – п/у.

Ответ: 2.

26 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия

19

Решение. (2 случай)
BC = 24, EF = 12, значит СЕ = BF = (24 – 12) : 2 = 6 (как средние линии ∆KLM и ∆NLM) ⟹ LM = 12;
KN = 2(CE + EF) = 2(6 + 12) = 36 (CF – средняя линия ∆KLN)
∆AKN ~ ∆ALM (по двум углам) ⟹ AL : AK = LM : KN = AM : AN.

Пусть AL = x, AM = y, тогда AK = 10 + x,
AN = 26 + y.
x : (10 + x) = 12 : 36 ⟹ x = 5;
y : (26 + y) = 12 : 36 ⟹ y = 13.
Значит, ∆AKN ~ ∆ALM – п/у.
AL = AK + KL = 5 + 10 = 15.

Ответ: 6.

x

y

Внутри него расположены две равные касающиеся окружности, каждая из которых

20

Внутри него расположены две равные касающиеся окружности, каждая из которых

6, AC = 7. Окружность, проходящая через точки A и

Решение. (1 случай)
∠ВАС + ∠KLC = 180° (по свойству трапеции, вписанной в окружность), ∠KLC = 180° − ∠ВАС ⟹
∠BLK = 180° − ∠KLС = ∠ВАС.
Аналогично, ∠ВKL = ∠ВСА ⟹
∆ВАС ~ ∆ВLK ⟹
BK : BC = BL : BA = KL : AC
BK : 6 = BL : 5 = KL : 7
KL + AC = AK + LC (по свойству трапеции,

описанной около окружности). Пусть BK = x, BL = y, тогда АК = 5 – х, BL = 6 – y.

21

шестиугольника) ⟹
окружности, описанные около этих ∆-ов имеют один и тот

22

центром O1,
касается внутренним образом одной окружности в точке M

По т. Пифагора в п/у ∆КO1О3

22

этого треугольника, в точке E. Окружность, описанная около треугольника ADE,

23

= CQ;
CK = CM; и т.д.
CN = CB +

⟹

⟹

S

стороны АВ и AD в точках M и N соответственно.

26

Решение.
а) по свойству касательных к окружности: KN = NQ; QM = MS;
P∆AMN = AM + MQ + QN + NA =
= AM + MS + KN + AN = AS + AK =
½ AB + ½ AD = AB, где S и К – точки касания окружности с квадратом или середины сторон квадрата.

АВ и AD в точках M и N соответственно.
а)

26

Решение.
б) Пусть сторона квадрата = 3х, AN = y.
Тогда AM = x, и MN = P∆AMN – x – y =
= 3x – x – y = 2x – y.
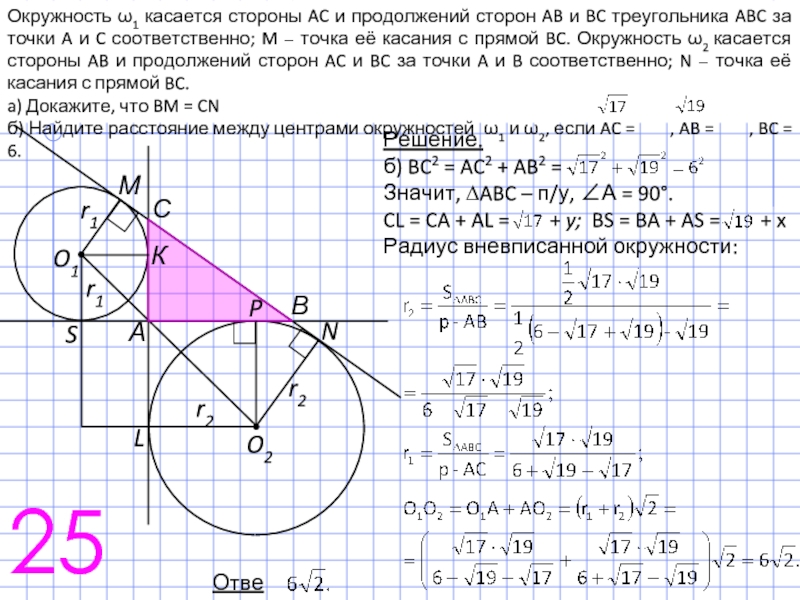
Радиус вневписанной окружности OE:




Откуда y = 0,75x, DN = 3x – 0,75x = 2,25x.
∆AMN ~ ∆DPN (по углам) ⟹
АM : DР = AN : DN; x : DP = 0,75x : 2,25x,
DP = 3x, EP = 4,5x, CP = 6x.
∆OEP ~ ∆LCP (по углам) ⟹
OE : CL = EP : CP; 1,5x : CL = 4,5x : 6x,
CL = 2x, LB = 3x – 2x = x ⟹ CL : BL = 2 : 1.

квадрат KLPQ. Прямая МР пересекает гипотенузу KL в точке N.
а)

27

Решение.
а) Продолжим прямые КМ и РL до пересечения в точке Е. Рассмотрим ∆КРЕ, в котором KL, РМ – медианы, по свойству которых KN : NL = PN : NM = 2 : 1.

Q

N

M

Р

L

K

E

квадрат KLPQ. Прямая МР пересекает гипотенузу KL в точке N.
а)

27

Решение.
б) Рассмотрим ∆NКR, ∆PLN – п/у.
∠KRN = ∠LNP
∆NKR ~ ∆PLN (по углам) ⟹
PL : KN = LN : KR;

этого треугольника, в точке E. Окружность, описанная около треугольника ADE,

29

Решение.

С

F

А

В

E

x

8

D

45°

3

сторон AB и AC лежат на одной окружности.
а) Докажите,

Решение.
а) PN – средняя линия ∆ABС ⟹ PN ∥ BC
∠PAM = ∠PNM (как вписанные в окружность углы, опирающиеся на одну дугу). ∠PNB = ∠CBN (как накрест лежащие при параллельных прямых)
∠MBK = ∠BAK, ∆AKB ~ ∆BKM (по двум углам, т.к. ∠К у них общий).

сторон AB и AC лежат на одной окружности.
а) Докажите,

Решение.
∆AKB ~ ∆BKM ⟹ КВ : АК = МК : КВ,
КВ2 = МК ∙ АК, т.к М – точка пересечения медиан, то АМ = 2КМ, АК = 3КМ,
КВ2 = МК ∙ 3МК = 3МК2


МК = 3, АК = 9.

Ответ: 9.