Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лобачевский и его геометрия 10 класс
Содержание
- 1. Лобачевский и его геометрия 10 класс
- 2. Гипотеза:Любая теория современной науки считается единственно верной,
- 3. Задачи:провести эксперимент «Иллюзии зрения»;изучить постулаты Евклидовой геометрии;изучить
- 4. Видите движение на этой картинке?
- 5. Эксперимент «Иллюзии зрения»На рисунке буквы расположены параллельно
- 6. Николай Иванович Лобачевский (1792 – 1856 гг.)Все!
- 7. Евклид (III век до н. э.) Древнегреческий
- 8. «Чем отличается геометрия Лобачевского от геометрии Евклида?»
- 9. Неевклидова геометрия единственно правильная?Нельзя сказать, что
- 10. ТЕСТПредлагаем Вашему вниманию тест. Вы можете его
- 11. Выводы Как показали исследования, геометрия
- 12. Список литературыСхоутен Я. А. Риманова геометрия, пер.
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лобачевский и его геометрия
Проблема:
Почему возникла "новая" геометрия?
Работу выполнили учащиеся
Слайд 2Гипотеза:
Любая теория современной науки считается единственно верной, пока не создана
следующая. Невозможность доказать некоторое геометрическое утверждение средствами евклидовой геометрии послужило
поводом построения другой геометрии, которая также является верной.Был мудрым Евклид,
Но его параллели,
Как будто бы вечные сваи легли.
И мысли его, что как стрелы летели,
Всегда оставались в пределах Земли.
А там, во вселенной, другие законы,
Там точками служат иные тела.
И там параллельных лучей миллионы
Природа сквозь Марс, может быть, провела.
Цель:
Найти доказательство того, что истинно утверждение «через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и параллельные ей»
Слайд 3Задачи:
провести эксперимент «Иллюзии зрения»;
изучить постулаты Евклидовой геометрии;
изучить аксиомы геометрии Лобачевского;
сделать
сравнительный анализ двух геометрий;
выяснить нет ли геометрий, основанных на других
аксиомах;сделать выводы.
Слайд 5Эксперимент «Иллюзии зрения»
На рисунке буквы расположены параллельно (стоят прямо) или
нет?
1
ИТОГИ опроса:
всего параллельно нет
300 3% 97%
Ответ: параллельно.
всего спираль окружности
300 100% 0%
Ответ: окружности.
На рисунке изображена спираль или несколько
окружностей?
2
ВЫВОД: В геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на наблюдения.
Положительный момент: благодаря зрительным искажениям существует живопись.
Если интересно
Слайд 6Николай Иванович Лобачевский
(1792 – 1856 гг.)
Все! Перечеркнуты “Начала”.
Довольно мысль
на них скучала,
Хоть прав почти во всем Евклид,
Но
быть не вечно постоянству: И плоскость свернута в пространство,
И мир
Иной имеет вид...
Краткое описание геометрии Лобачевского.
ВЫВОД: Заменив V постулат евклидовой геометрии на аксиому, Лобачевский пришел к выводу, что можно построить другую геометрию, отличную от евклидовой.
Слайд 7Евклид (III век до н. э.) Древнегреческий математик, автор первого трактата
по геометрии «Начала» (в 13 книгах).
В основе всей геометрии греческого
математика ЕвклидаВ основе всей геометрии греческого математика Евклида В основе всей геометрии греческого математика Евклида лежало несколько простых первоначальных утверждений (аксиом), которые принимались за истинные без доказательств. Из аксиом путем доказательств выводились более сложные утверждения, из тех выводились еще более сложные. Особый интерес математиков всегда вызывала пятая аксиома о параллельных прямых. В отличие от остальных аксиом элементарной геометрии, аксиома параллельных не обладает свойством непосредственной очевидности. Поэтому на всем протяжении истории геометрии имели место попытки доказать аксиому параллельных, то есть вывести ее из остальных аксиом геометрии.
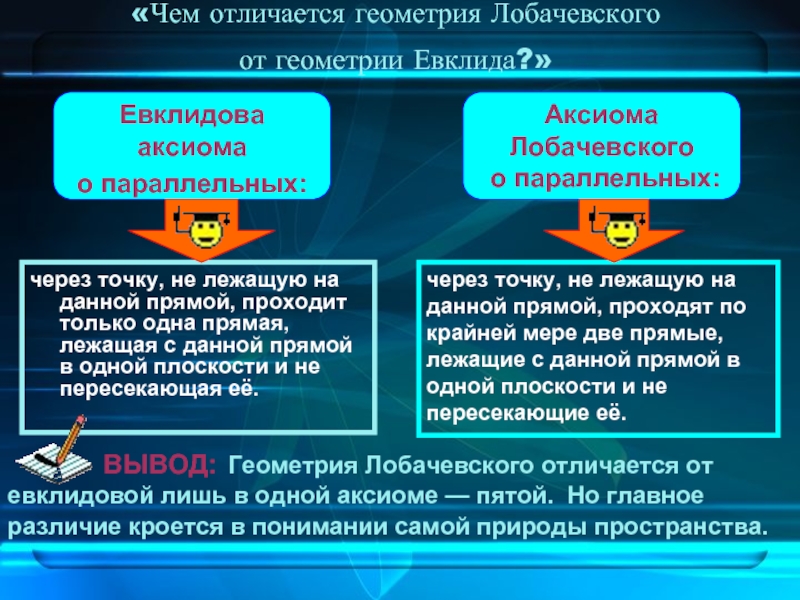
Слайд 8«Чем отличается геометрия Лобачевского
от геометрии Евклида?»
через точку, не лежащую
на данной прямой, проходит только одна прямая, лежащая с данной
прямой в одной плоскости и не пересекающая её.через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
ВЫВОД: Геометрия Лобачевского отличается от евклидовой лишь в одной аксиоме — пятой. Но главное различие кроется в понимании самой природы пространства.
Евклидова аксиома
о параллельных:
Аксиома
Лобачевского
о параллельных:
Слайд 9Неевклидова геометрия
единственно правильная?
Нельзя сказать, что неевклидова геометрия единственно правильная.
На данный момент к ней нет никаких претензий. Но, может
быть, через много лет она устареет – или это произойдет быстрее? Так или иначе, но наука никогда не будет стоять на месте.Геометрия Лобачевского не единственная, существуют и другие, например Римана геометрия:
Риманова геометрия, многомерное обобщение геометрии на поверхности, представляющее собой теорию римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка сравнительно с размерами области). Риманова геометрия получила своё название по имени Б. Римана, который заложил её основы в 1854.
Слайд 10ТЕСТ
Предлагаем Вашему вниманию тест. Вы можете его выполнить в том
случае, если уже прошли курс геометрии 7 класса.
Задание
Слайд 11Выводы
Как показали исследования, геометрия Лобачевского (в то
числе и 5-ый постулат) совершенно верна, если ее рассматривать не
на плоскости, а на поверхности гиперболического параболоида (вогнутой поверхности, напоминающей седло).Любая теория современной науки считается единственно верной, пока не создана следующая. Это своеобразная аксиома развития науки.
Слайд 12Список литературы
Схоутен Я. А. Риманова геометрия, пер. с англ., М.,
1948;
Колесников М. Лобачевский./. Серия «Жизнь замечательных людей». – М.: Молодая
гвардия, 1965. – 320 стр. с илл. Широков П.А. Краткий очерк основ геометрии Лобачевского./. – М.: Наука, 1983. – 76 стр.
Лобачевский Н.И. Полное собрание сочинений, тт. 1–5. М. – Л., 1946–1951
Геометрия Лобачевского. Материал из Википедии — свободной энциклопедии
Web ресурсы
http://www.pereplet.ru/obrazovanie/stsoros/67.html - о неевклидовой геометрии, Э. Б. ВИНБЕРГ, Московский государственный университет им.
М.В. Ломоносова
http://www.hrono.ru/biograf/lobachevski.html - Шикман А.П. Деятели отечественной истории. Биографический справочник. Москва, 1997 г.
http://ns.math.rsu.ru/mexmat/polesno/evklid.ru.html - биография Евклида.