аттестации
ЦЕЛИ УРОКА:
обобщить и систематизировать полученные и приобретенные знания, умения,
навыки;активация элементов ранее изученного материала;
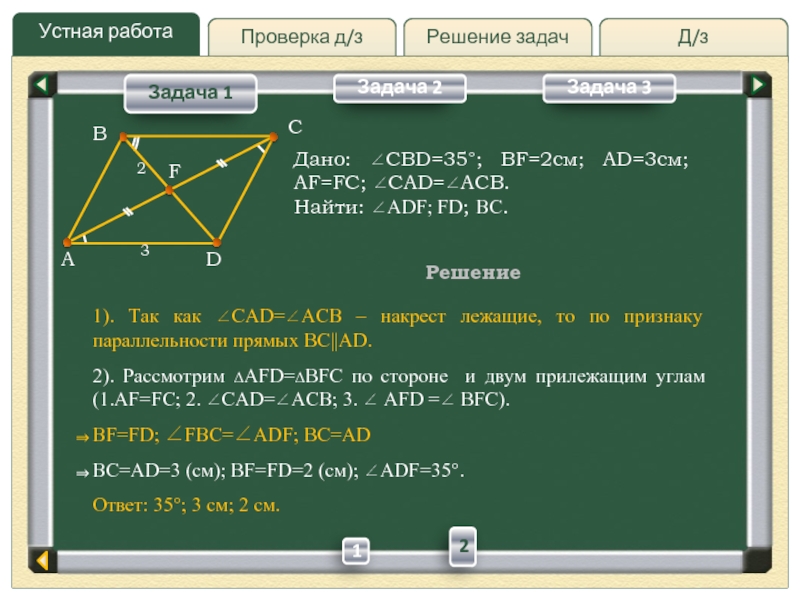
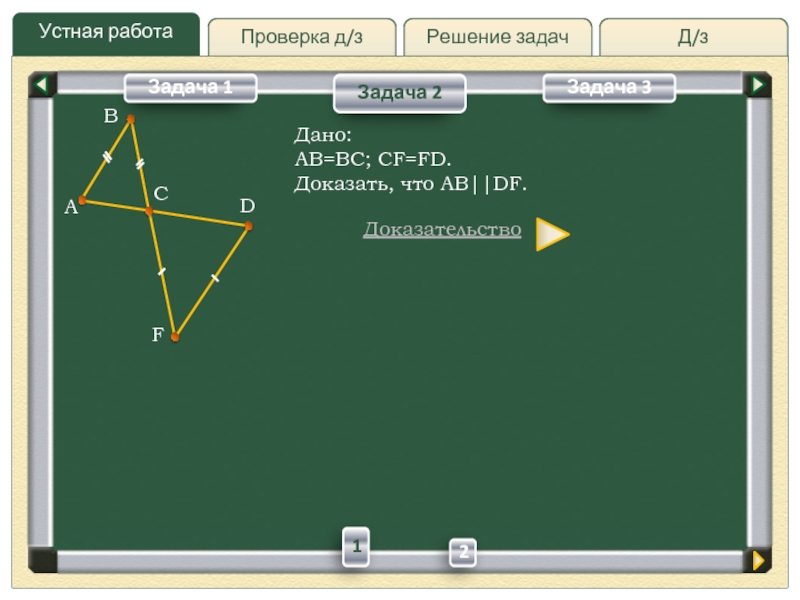
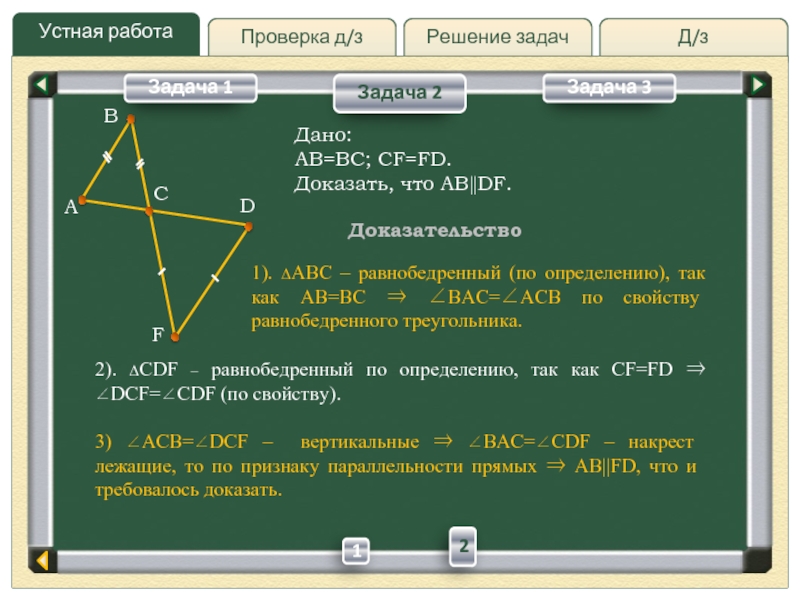
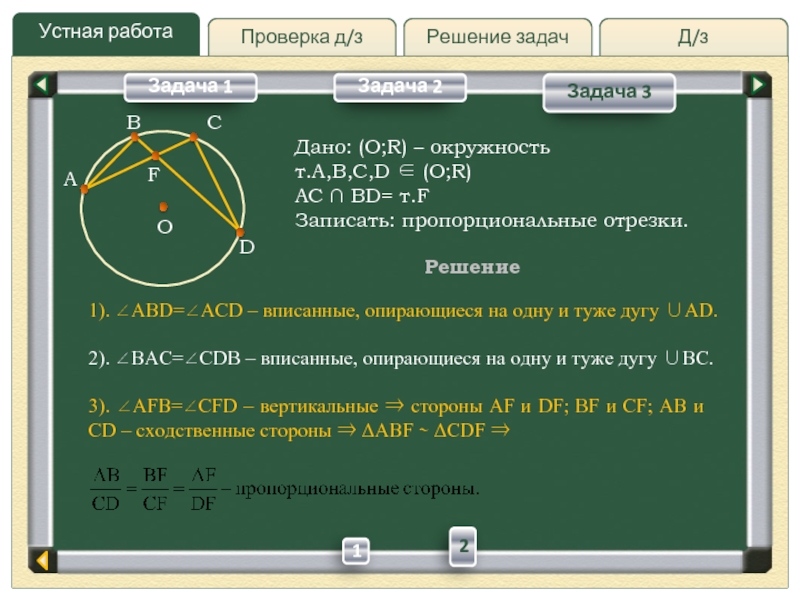
повторить свойства фигур, рассмотреть различные способы расположения геометрических фигур на плоскости;
при решении стандартных задач рассматривать возможность другой конфигурации фигур.
АВТОРЫ:
Веприкова Римма Хабибулаевна (учитель математики)
Зайцева Вера Васильевна (учитель информатики)
МОУ – Гимназия № 2 г. Клин Московской области