Слайд 22
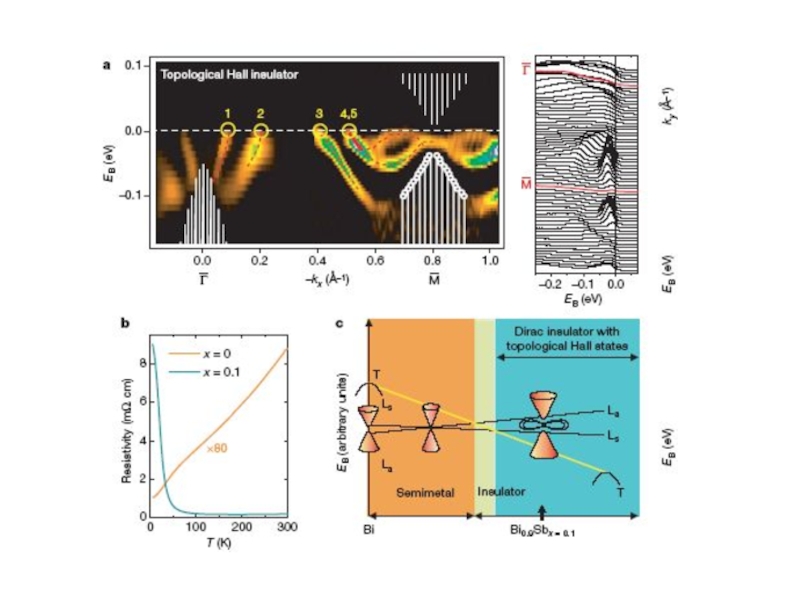
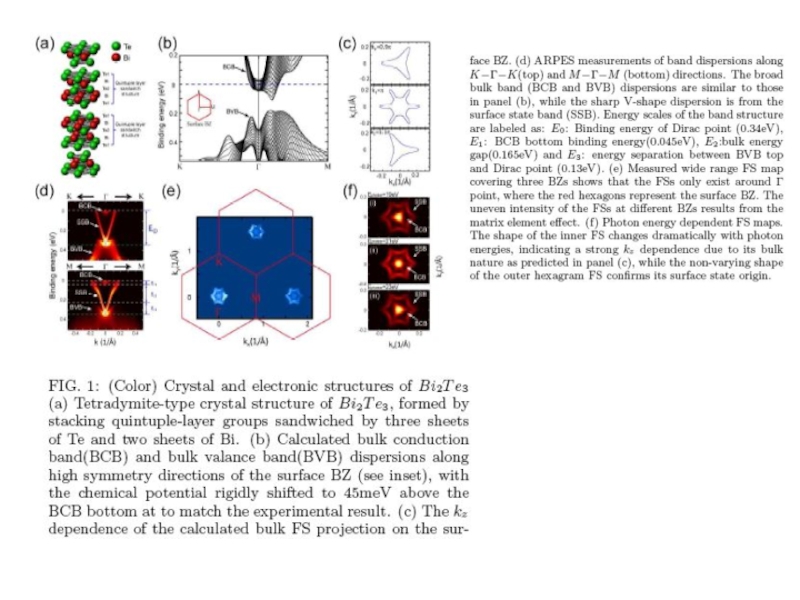
Large Gap Topological Insulator Bi2Te3 with a Single Dirac Cone
on the Surface
Y. L. ChenY. L. Chen, J.
G. AnalytisY. L. Chen, J. G. Analytis, J. H. ChuY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. LiuY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. MoY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. QiY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. ZhangY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. LuY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. DaiY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. FangY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. ZhangY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. FisherY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. Fisher, Z. HussainY. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. Fisher, Z. Hussain, Z. X. Shen
arXiv:0904.1829

Слайд 26Транспортные эксперименты
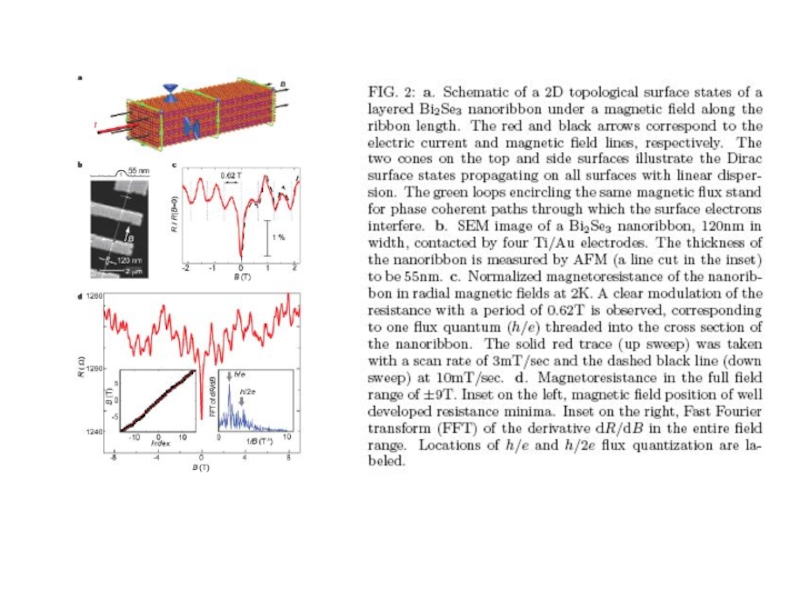
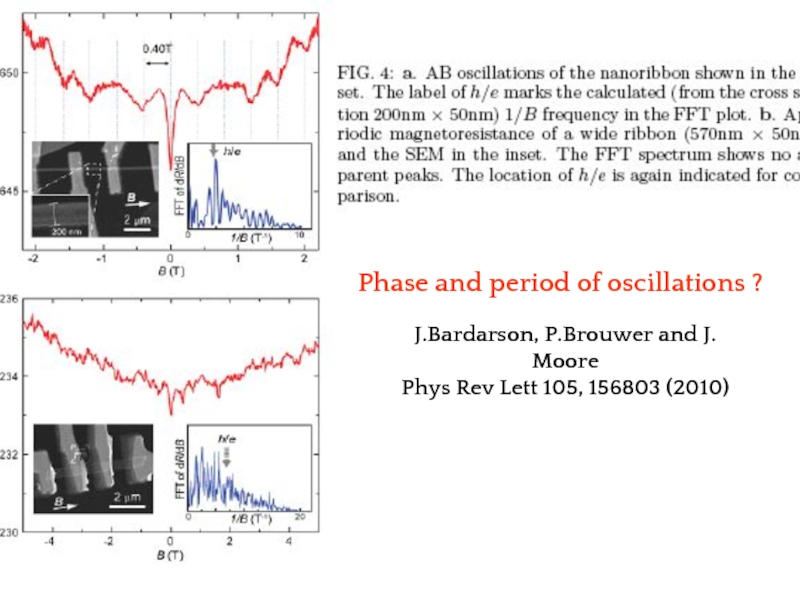
Aharonov-Bohm interference in topological insulator nanoribbons
Hailin PengHailin Peng,
Keji LaiHailin Peng, Keji Lai, Desheng KongHailin Peng, Keji Lai,
Desheng Kong, Stefan MeisterHailin Peng, Keji Lai, Desheng Kong, Stefan Meister, Yulin Chen,
Xiao-Liang Qi Xiao-Liang Qi, Shou-Cheng Zhang Xiao-Liang Qi, Shou-Cheng Zhang, Zhi-Xun Shen Xiao-Liang Qi, Shou-Cheng Zhang, Zhi-Xun Shen, Yi Cui
arXiv:0908.3314
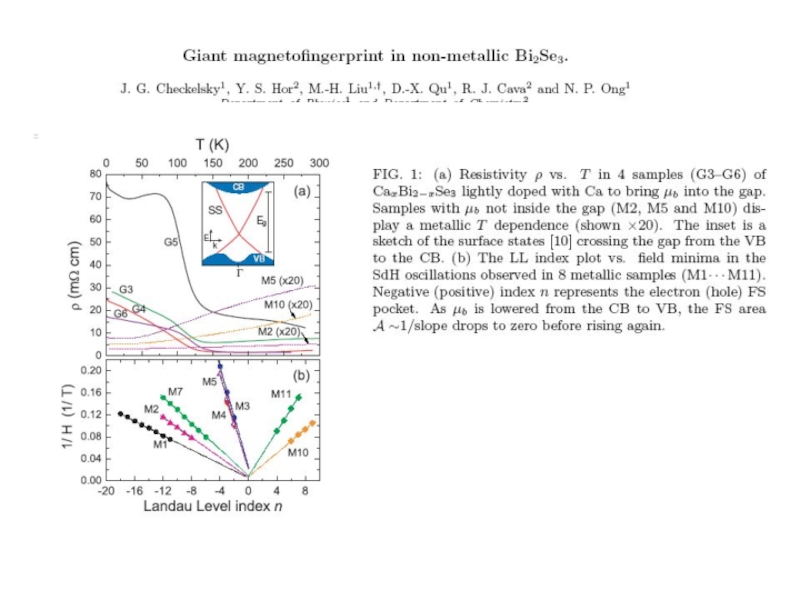
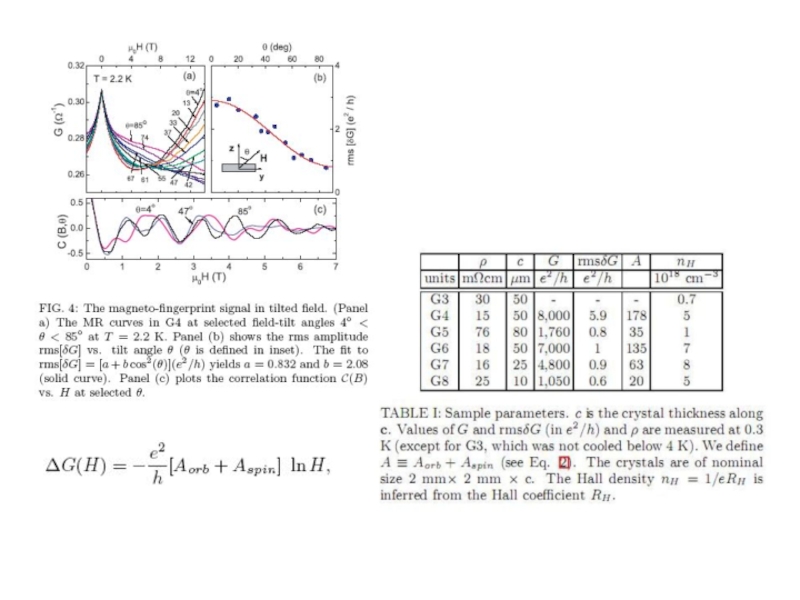
Giant magnetic fingerprint in non-metallic Bi2Se3
J.Checkelsky et al arXiv:0909.1840
Superconductivity in CuxBi2Se3 and its implications for pairing in the
undoped topological insulator Y. S. Hor Y. S. Hor, A. J. Williams Y. S. Hor, A. J. Williams, J. G. Checkelsky,
P. RoushanP. Roushan, J. SeoP. Roushan, J. Seo, Q. XuP. Roushan, J. Seo, Q. Xu, H. W. ZandbergenP. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. YazdaniP. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. Yazdani, N. P. OngP. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. Yazdani, N. P. Ong, R. J. Cava
arXiv:0909.2890
Nonlocal transport in quantum spin-Hall state in HgTe quantum well
Слайд 53Индуцированная сверхпроводимость и майорановские состояния
Superconducting Proximity Effect and Majorana Fermions
at the Surface of a Topological Insulator
Phys. Rev.
Lett. 100, 096407 (2008) L. FuL. Fu and C. L. Kane
Они же: arXiv:0804.4469, arXiv:0903.2427
Phys. Rev. Lett. 102, 216404 (2009) Electrically Detected Interferometry of Majorana Fermions in a Topological Insulator A. R. AkhmerovA. R. Akhmerov, Johan NilssonA. R. Akhmerov, Johan Nilsson, and C. W. J. Beenakker
Manipulation of Majorana fermion, Andreev reflection and Josephson current on topological insulators Yukio TanakaYukio Tanaka, Takehito YokoyamaYukio Tanaka, Takehito Yokoyama, Naoto Nagaosa arXiv:0907.2088
Majorana Fermion Induced Resonant Andreev Reflection K. T. LawMajorana Fermion Induced Resonant Andreev Reflection K. T. Law, Patrick A. LeeMajorana Fermion Induced Resonant Andreev Reflection K. T. Law, Patrick A. Lee, T. K. Ng arXiv:0907.1909
Detecting Majorana bound states induced by a topological insulator
Colin Benjamin Colin Benjamin, Jiannis K. Pachos arXiv:0908.0655