Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
{ ЛЕКЦИЯ 5 } { Алгоритмы на графах }
Содержание
- 1. { ЛЕКЦИЯ 5 } { Алгоритмы на графах }
- 2. { Графы }Задача маршрутизации (задача коммивояжёра). Анализ игр. Анализ алгоритмов. Задача о максимальном потоке.
- 3. { Графы }Граф - абстрактный математический объект,
- 4. { Очередь и стек. }В Python стеком
- 5. { Очередь и cтек в Python. }queue
- 6. { Представление графов }Граф может быть представлен:Множеством смежностиСписком рёбер {откуда, куда, стоимость}: ГрафическиМатрицей смежности
- 7. { Обход графа }Во многих приложениях нужно
- 8. { Что даёт поиск }Поиск в глубину
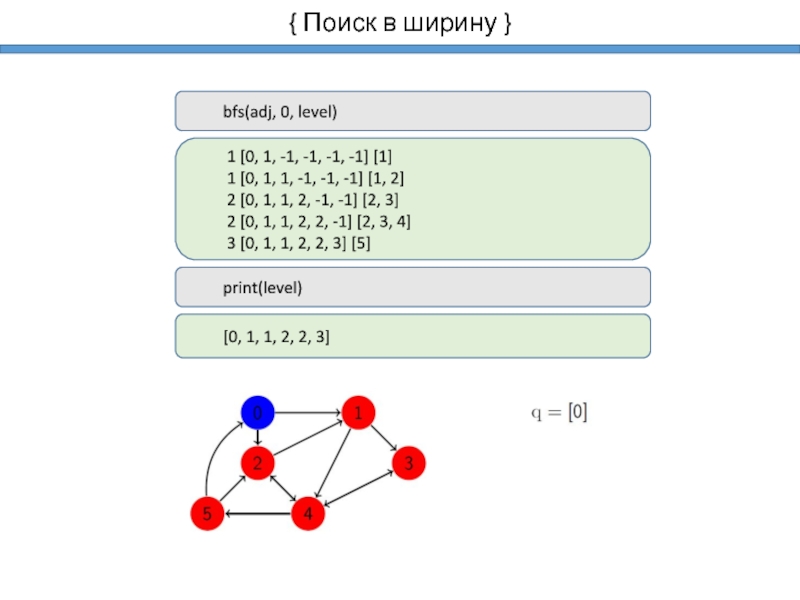
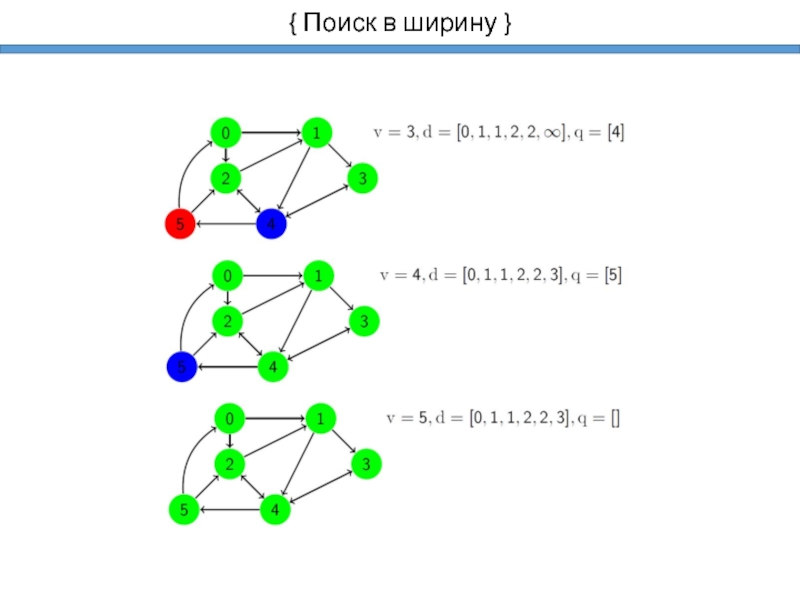
- 9. { Поиск в ширину }
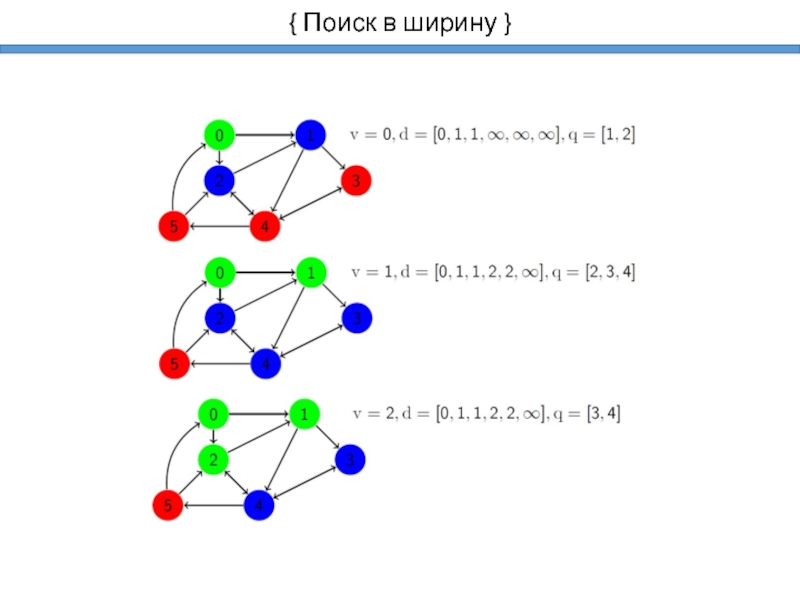
- 10. { Поиск в ширину }
- 11. { Поиск в ширину }
- 12. { Поиск в ширину }
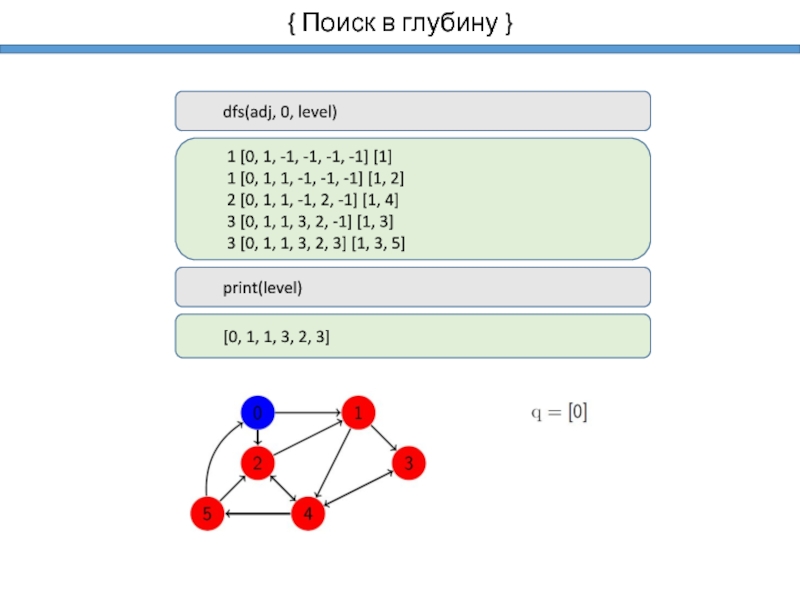
- 13. { Поиск в глубину }
- 14. { Поиск в глубину }
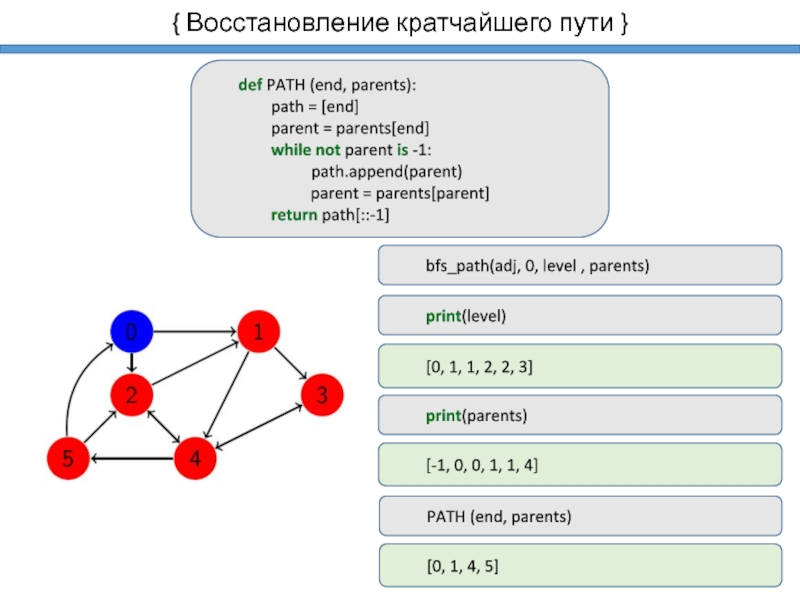
- 15. { Восстановление кратчайшего пути }
- 16. { Восстановление кратчайшего пути }
- 17. { Ход конём }По каким клеткам должен
- 18. { Алгоритм Дейкстры }Часто нужно уметь вычислять
- 19. { Алгоритм Дейкстры }
- 20. { Алгоритм Дейкстры }Массивы:массив a, такой что
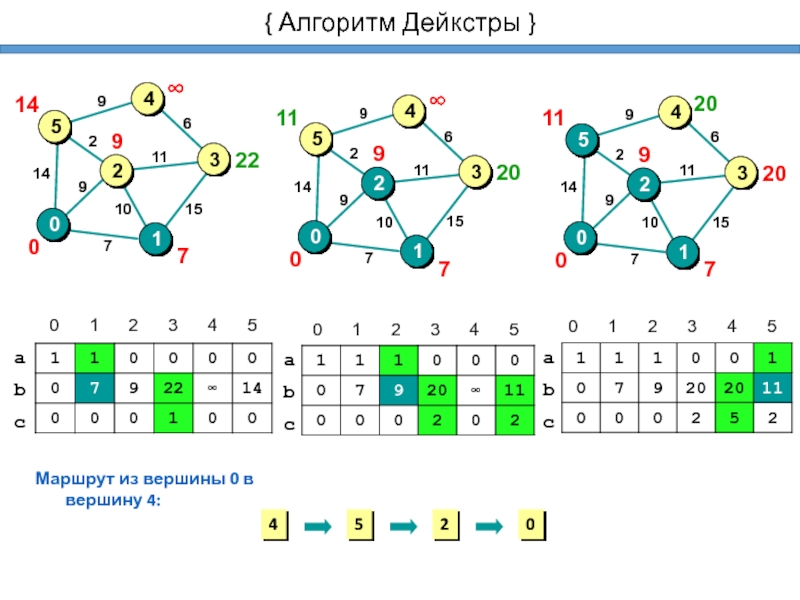
- 21. { Алгоритм Дейкстры }Маршрут из вершины 0 в вершину 4:
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2{ Графы }
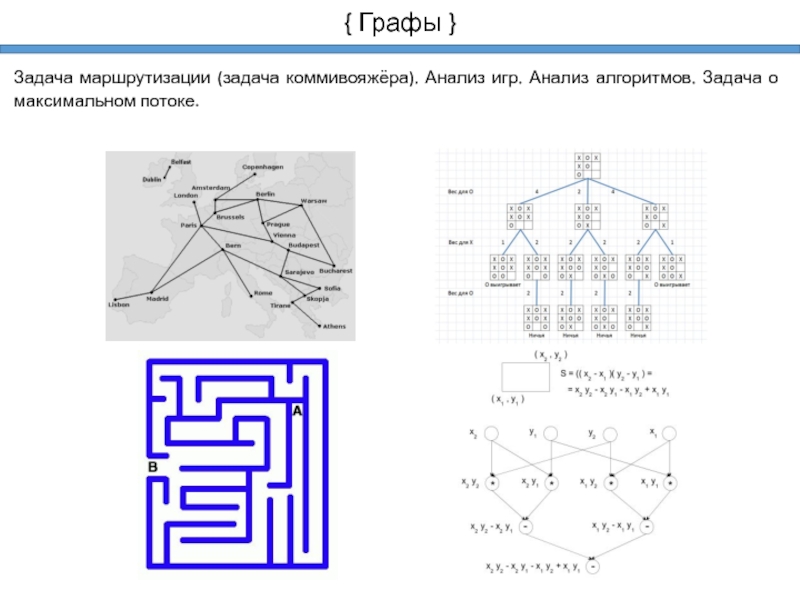
Задача маршрутизации (задача коммивояжёра). Анализ игр. Анализ алгоритмов.
Задача о максимальном потоке.
Слайд 3{ Графы }
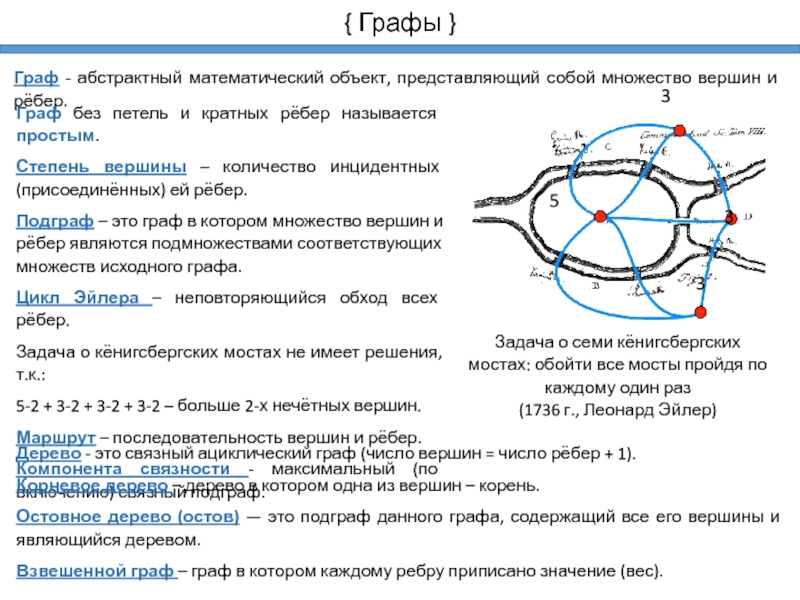
Граф - абстрактный математический объект, представляющий собой множество
вершин и рёбер.
Задача о семи кёнигсбергских мостах: обойти все мосты
пройдя по каждому один раз(1736 г., Леонард Эйлер)
Граф без петель и кратных рёбер называется простым.
Степень вершины – количество инцидентных (присоединённых) ей рёбер.
Подграф – это граф в котором множество вершин и рёбер являются подмножествами соответствующих множеств исходного графа.
Цикл Эйлера – неповторяющийся обход всех рёбер.
Задача о кёнигсбергских мостах не имеет решения, т.к.:
5-2 + 3-2 + 3-2 + 3-2 – больше 2-х нечётных вершин.
Маршрут – последовательность вершин и рёбер.
Компонента связности - максимальный (по включению) связный подграф.
5
3
3
3
Дерево - это связный ациклический граф (число вершин = число рёбер + 1).
Корневое дерево – дерево в котором одна из вершин – корень.
Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом.
Взвешенной граф – граф в котором каждому ребру приписано значение (вес).
Слайд 4{ Очередь и стек. }
В Python стеком можно сделать любой
список, так как для них доступны операции pop и push.
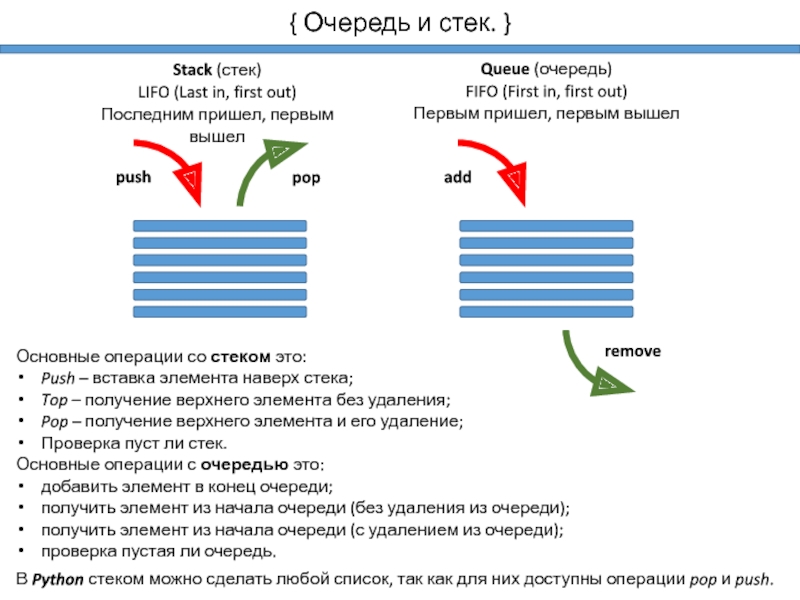
Stack
(стек)LIFO (Last in, first out)
Последним пришел, первым вышел
Queue (очередь)
FIFO (First in, first out)
Первым пришел, первым вышел
Основные операции со стеком это:
Push – вставка элемента наверх стека;
Top – получение верхнего элемента без удаления;
Pop – получение верхнего элемента и его удаление;
Проверка пуст ли стек.
Основные операции с очередью это:
добавить элемент в конец очереди;
получить элемент из начала очереди (без удаления из очереди);
получить элемент из начала очереди (с удалением из очереди);
проверка пустая ли очередь.
Слайд 5{ Очередь и cтек в Python. }
queue = list(range(1,22,3))
print(queue)
queue =
list(range(1,22,3))
print(queue)
i=0
%%time
x = queue[i]
i+=1
Не эффективно по времени
Не эффективно по памяти
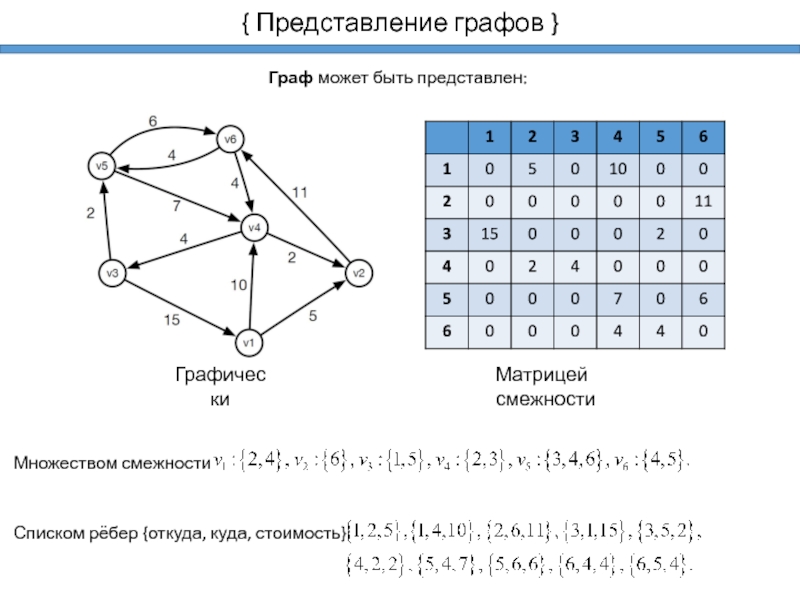
Слайд 6{ Представление графов }
Граф может быть представлен:
Множеством смежности
Списком рёбер {откуда,
куда, стоимость}:
Графически
Матрицей смежности
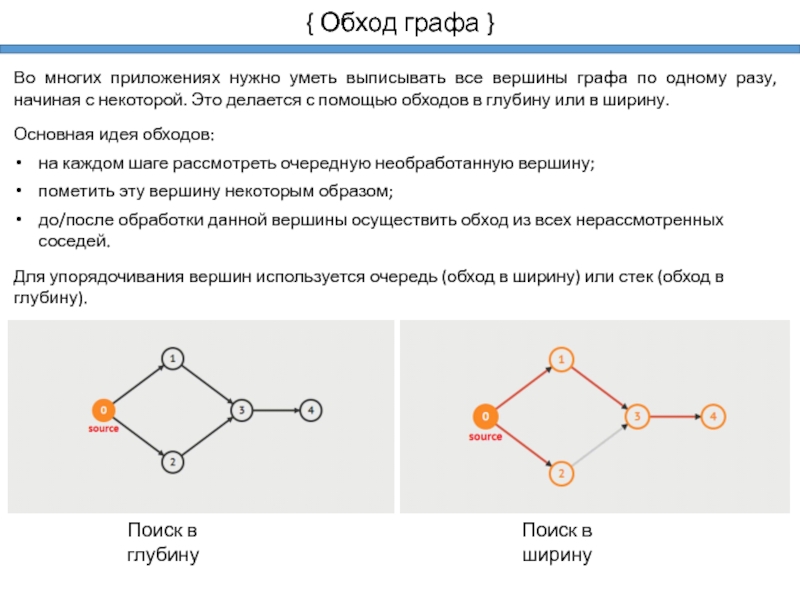
Слайд 7{ Обход графа }
Во многих приложениях нужно уметь выписывать все
вершины графа по одному разу, начиная с некоторой. Это делается
с помощью обходов в глубину или в ширину.Основная идея обходов:
на каждом шаге рассмотреть очередную необработанную вершину;
пометить эту вершину некоторым образом;
до/после обработки данной вершины осуществить обход из всех нерассмотренных соседей.
Для упорядочивания вершин используется очередь (обход в ширину) или стек (обход в глубину).
Поиск в глубину
Поиск в ширину
Слайд 8{ Что даёт поиск }
Поиск в глубину можно использовать для:
выделение
компонент связности (подсчёт компонент);
поиск простого цикла.
Поиск в ширину можно использовать
для:выделение компонент связности (подсчёт компонент);
поиск кратчайшего пути в невзвешенном графе;
восстановление кратчайшего пути;
нахождение кратчайшего цикла в ориентированном невзвешенном графе.
Слайд 17{ Ход конём }
По каким клеткам должен пройти конь перемещаясь
между клетками d4 и f2?
Сведем задачу к графу, пройдем его
в ширину и восстановим кратчайший путь.Слайд 18{ Алгоритм Дейкстры }
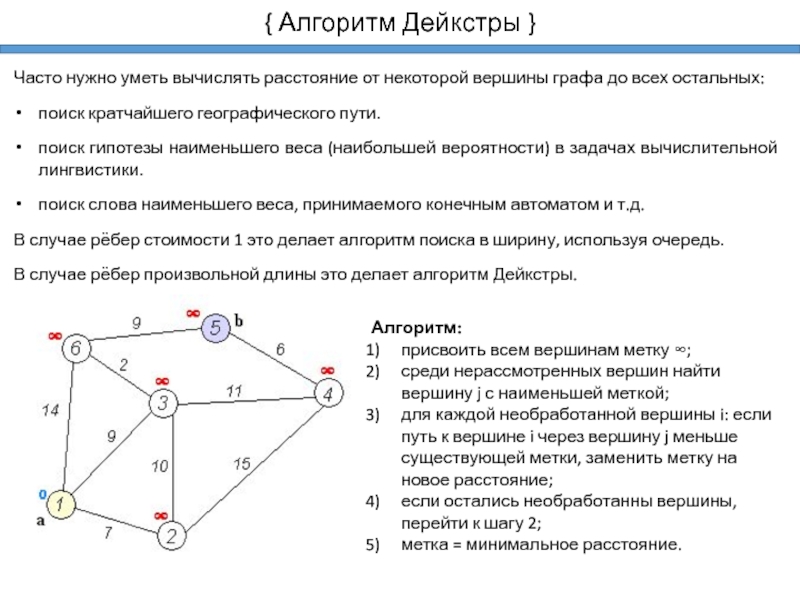
Часто нужно уметь вычислять расстояние от некоторой
вершины графа до всех остальных:
поиск кратчайшего географического пути.
поиск гипотезы наименьшего
веса (наибольшей вероятности) в задачах вычислительной лингвистики.поиск слова наименьшего веса, принимаемого конечным автоматом и т.д.
В случае рёбер стоимости 1 это делает алгоритм поиска в ширину, используя очередь.
В случае рёбер произвольной длины это делает алгоритм Дейкстры.
Алгоритм:
присвоить всем вершинам метку ∞;
среди нерассмотренных вершин найти вершину j с наименьшей меткой;
для каждой необработанной вершины i: если путь к вершине i через вершину j меньше существующей метки, заменить метку на новое расстояние;
если остались необработанны вершины, перейти к шагу 2;
метка = минимальное расстояние.
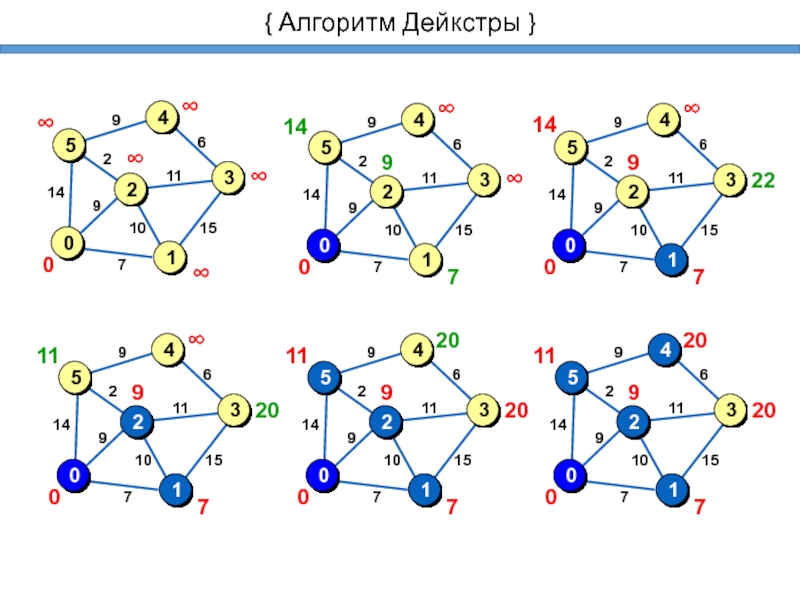
Слайд 20{ Алгоритм Дейкстры }
Массивы:
массив a, такой что a[i]=1, если вершина
уже рассмотрена, и a[i]=0, если нет.
массив b, такой что b[i]
– длина текущего кратчайшего пути из заданной вершины x в вершину i;массив c, такой что c[i] – номер вершины, из которой нужно идти в вершину i в текущем кратчайшем пути.
Инициализация:
заполнить массив a нулями (вершины не обработаны);
записать в b[i] значение W[x][i];
заполнить массив c значением x;
записать a[x]=1.
Основной цикл:
если все вершины рассмотрены, то стоп.
среди всех нерассмотренных вершин (a[i]=0) найти вершину j, для которой b[i] – минимальное;
записать a[j]=1;
для всех вершин k: если путь в вершину k через вершину j короче, чем найденный ранее кратчайший путь, запомнить его: записать b[k]=b[j]+W[j][k] и c[k]=j.

![{ ЛЕКЦИЯ 5 } { Алгоритмы на графах } { Очередь и cтек в Python. }queue = list(range(1,22,3))print(queue)queue = list(range(1,22,3))print(queue)i=0%%time { Очередь и cтек в Python. }queue = list(range(1,22,3))print(queue)queue = list(range(1,22,3))print(queue)i=0%%time x = queue[i]i+=1Не эффективно по времениНе](/img/thumbs/3ab37727027d562aa4dbcd4687158bfb-800x.jpg)





![{ ЛЕКЦИЯ 5 } { Алгоритмы на графах } { Алгоритм Дейкстры }Массивы:массив a, такой что a[i]=1, если вершина уже { Алгоритм Дейкстры }Массивы:массив a, такой что a[i]=1, если вершина уже рассмотрена, и a[i]=0, если нет.массив b,](/img/thumbs/c68bf6f83c957819c4d0d29b50cdbf59-800x.jpg)