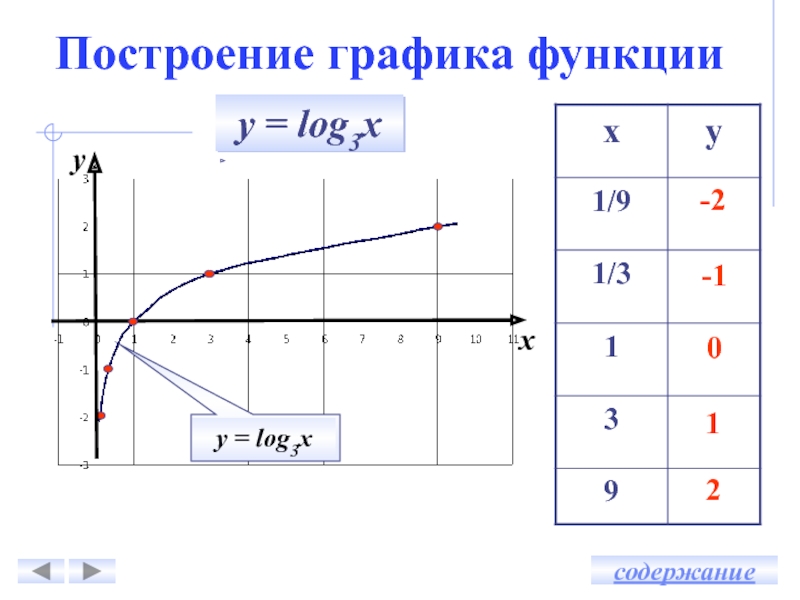
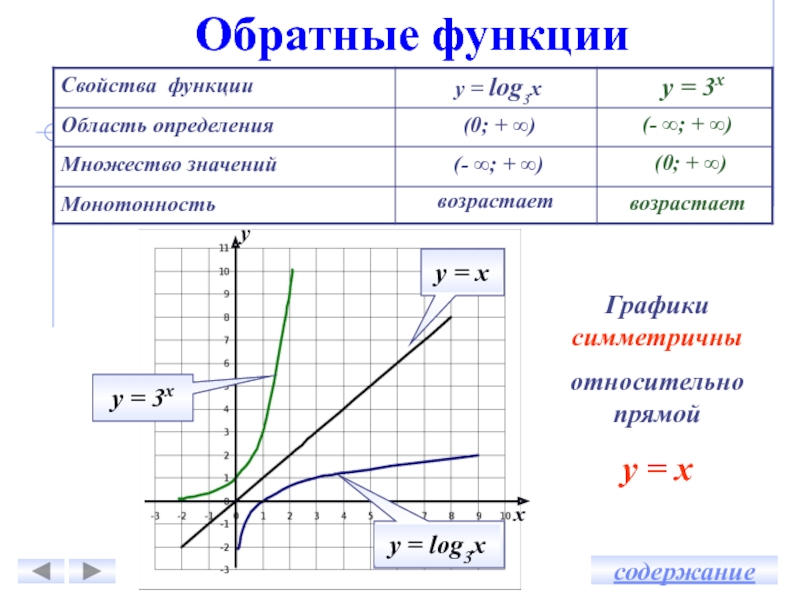
log3х
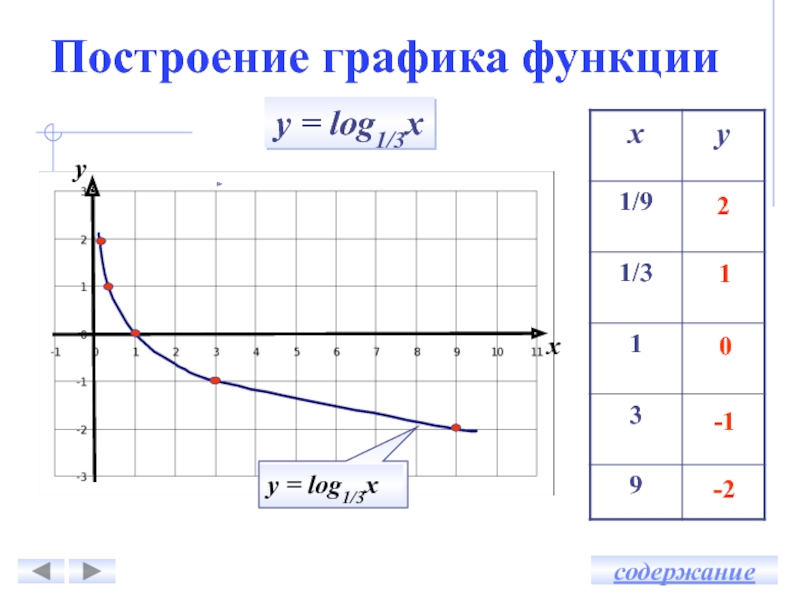
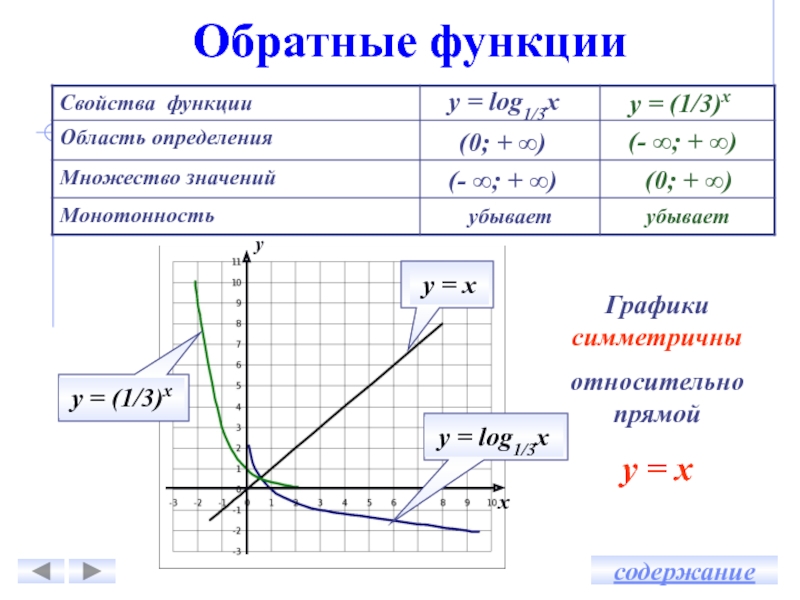
Построение графика у = log1/3х
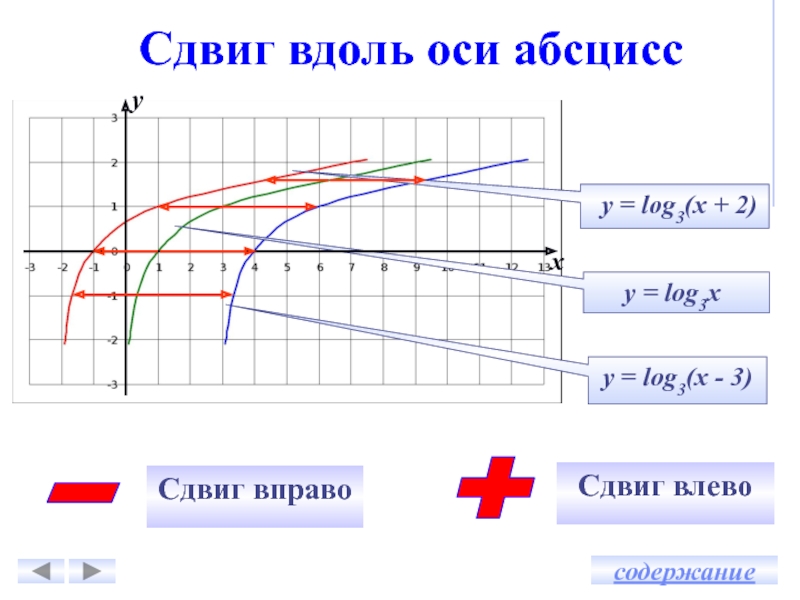
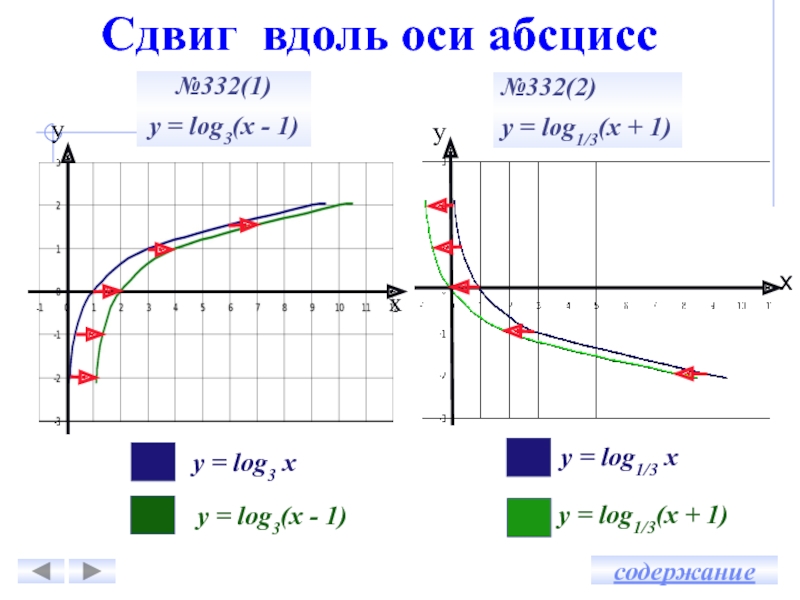
Сдвиг вдоль оси абсцисс
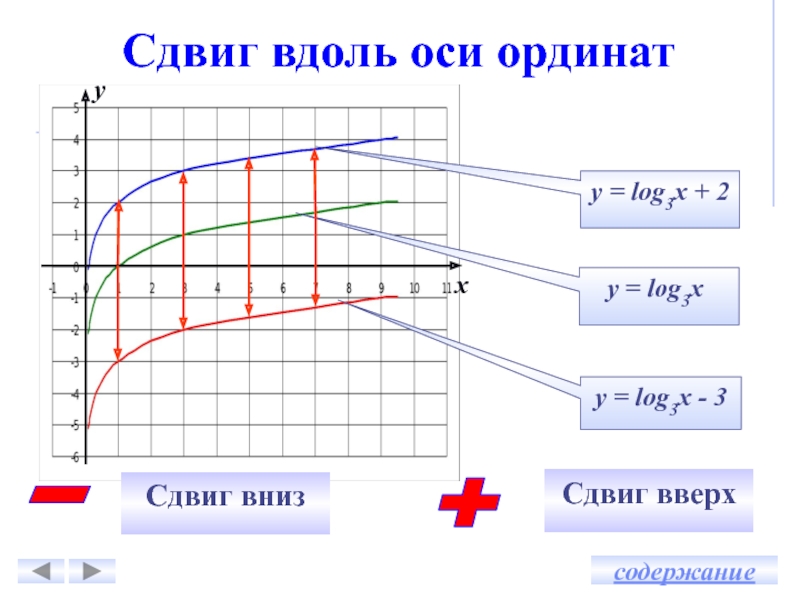
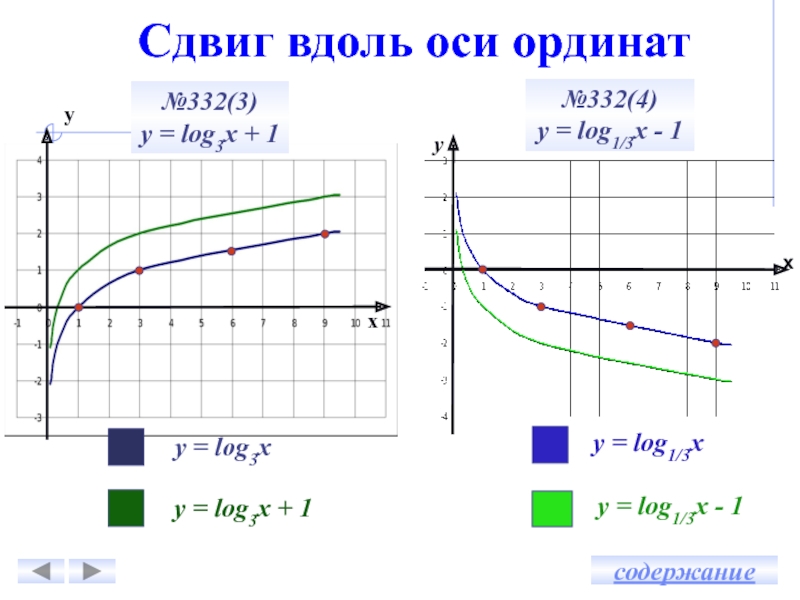
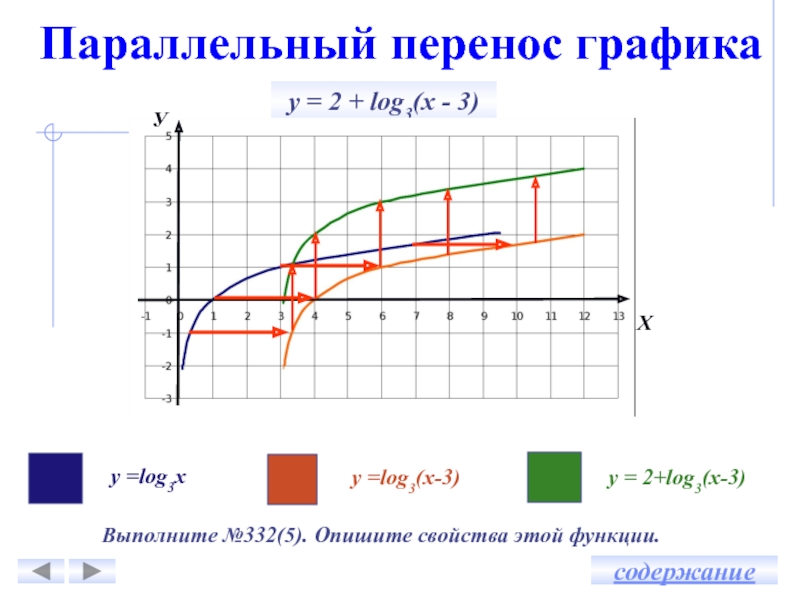
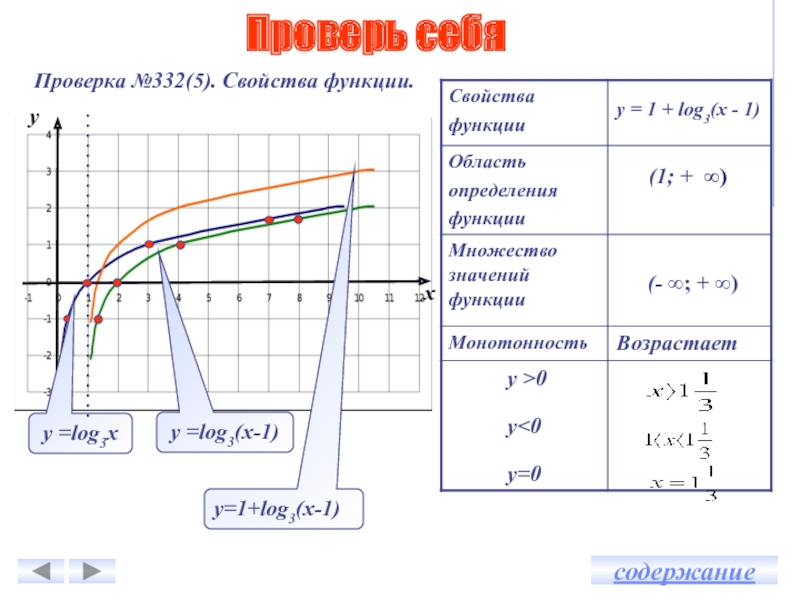
Сдвиг вдоль оси ординатПараллельный перенос графика
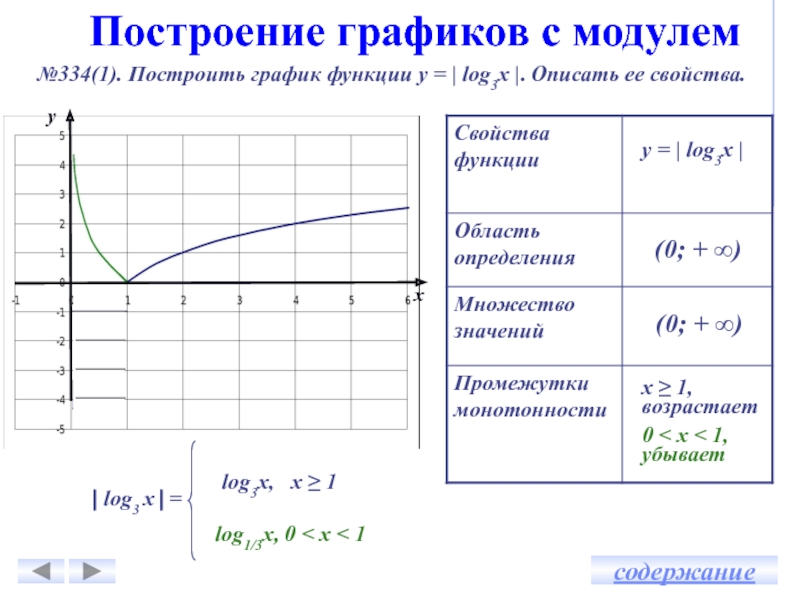
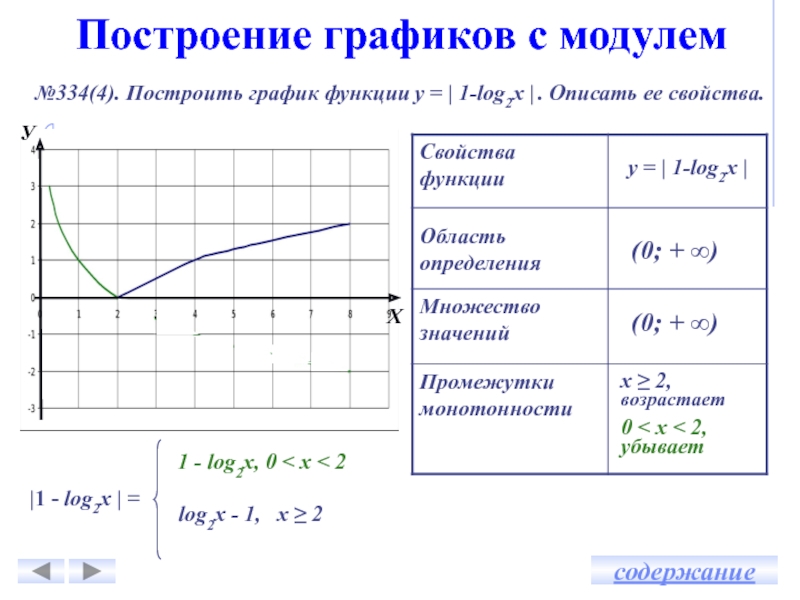
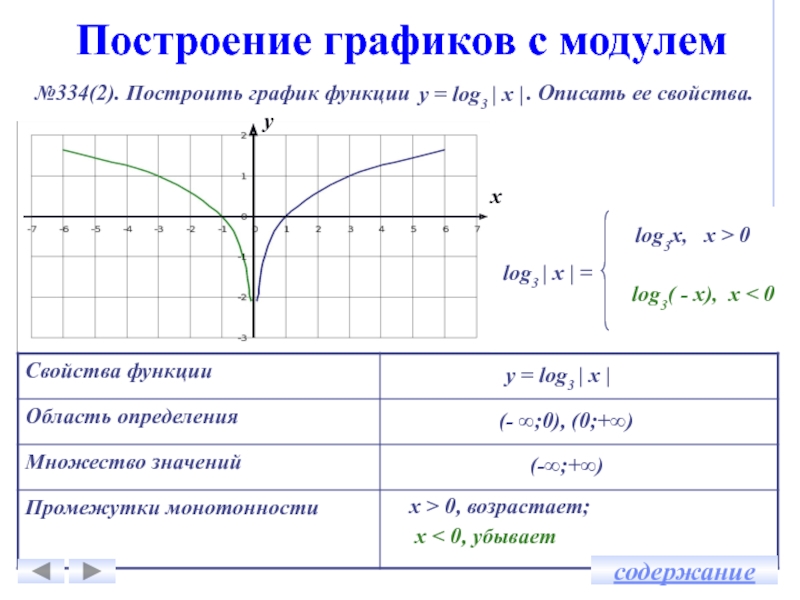
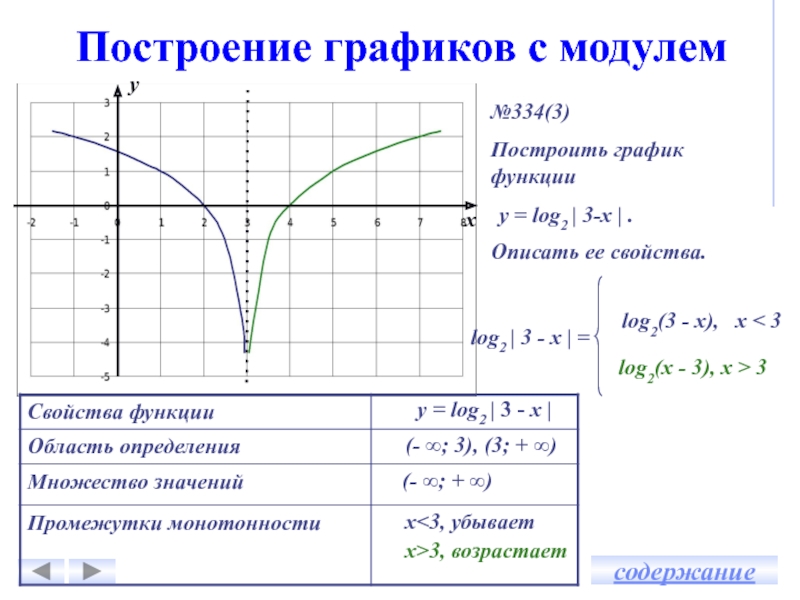
Построение графика с модулем
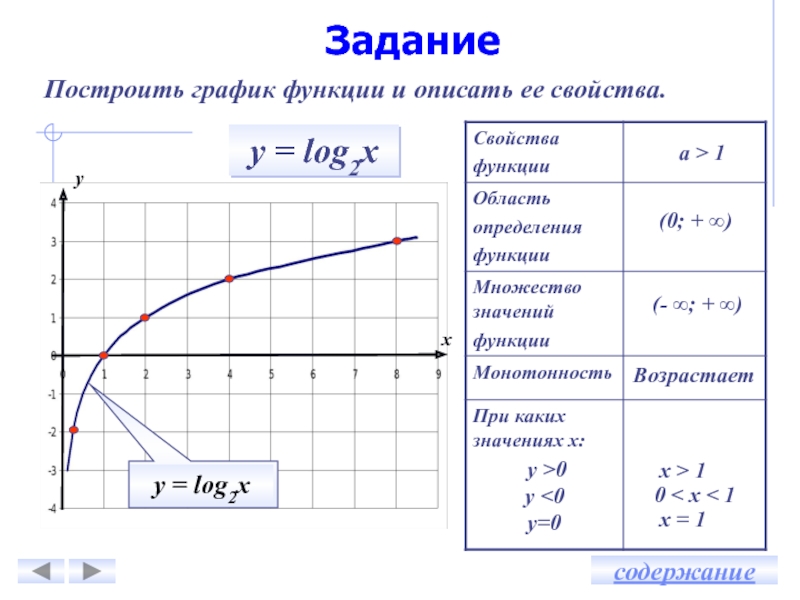
Задания
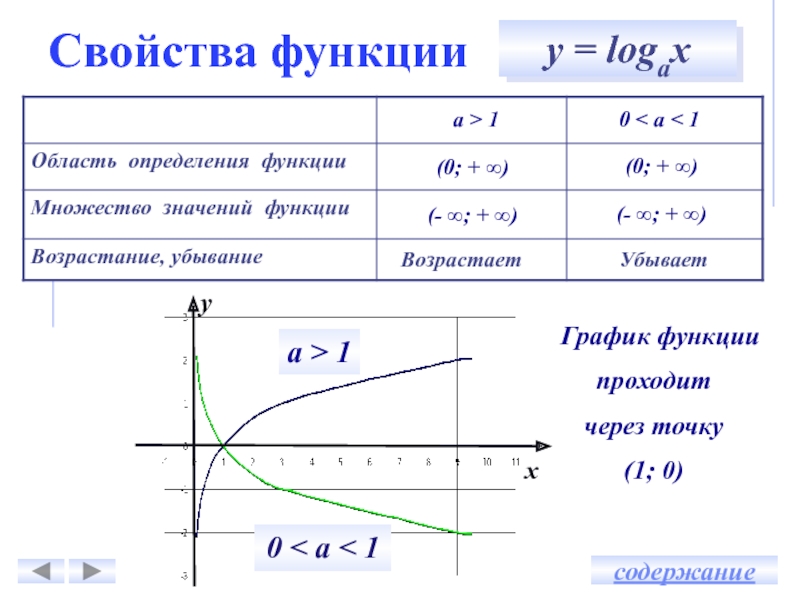
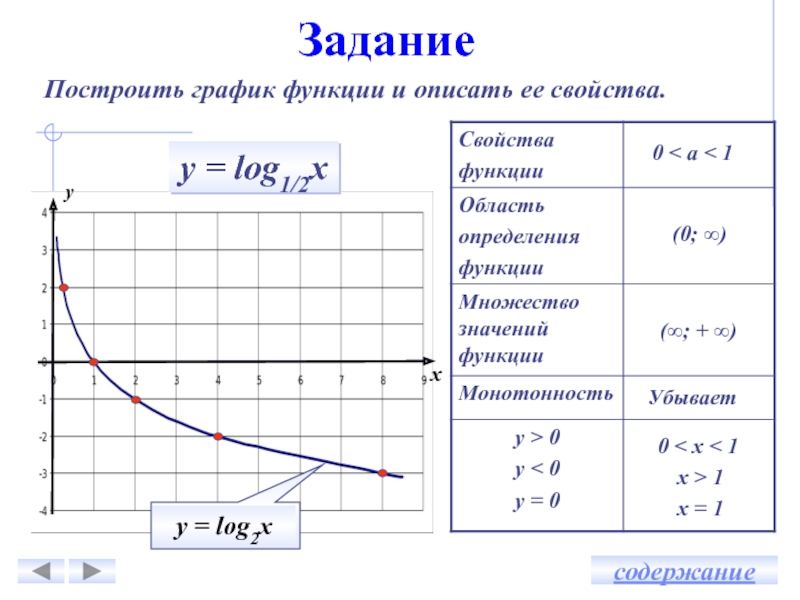
Функция
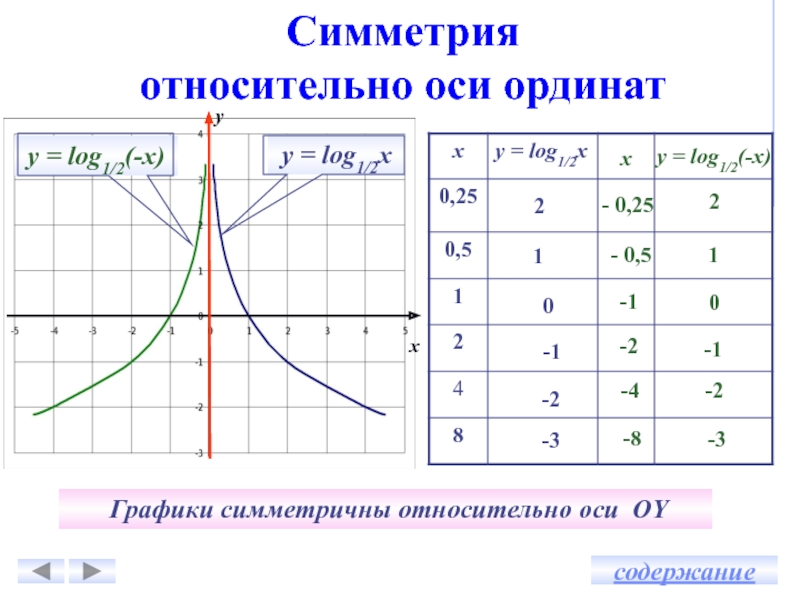
у = logах