Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 1. Статически определимые и неопределимые задачи Задача считается статически
Содержание
- 1. 1 1. Статически определимые и неопределимые задачи Задача считается статически
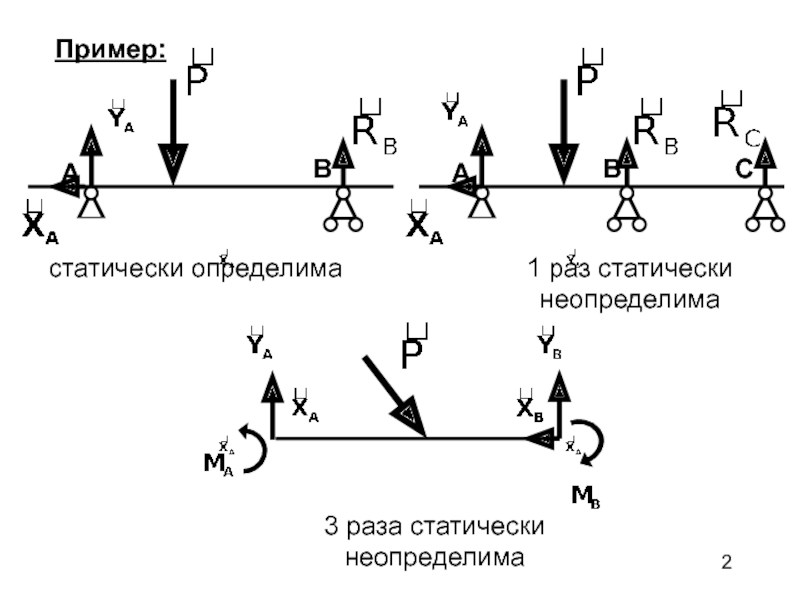
- 2. ABПример:AСBстатически определима1 раз статически неопределима3 раза статически неопределима
- 3. Ферма – конструкция, состоящая из большого числа
- 4. Простейшая ферма – ферма из 3-х узлов.Простая
- 5. Фермы (метод вырезания узлов)S = 2n -
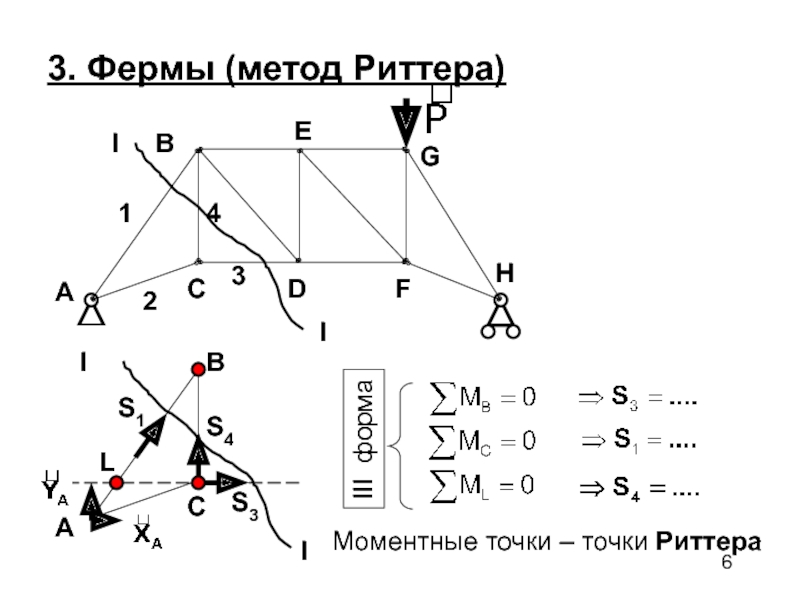
- 6. 3. Фермы (метод Риттера)IIACBIIS1S3S4III формаLМоментные точки – точки Риттера
- 7. Пространственная система сил1. Момент силы относительно осиzh0если1.2.пересекаетТ.е. сила и ось лежат в одной плоскостиПравило знаков:
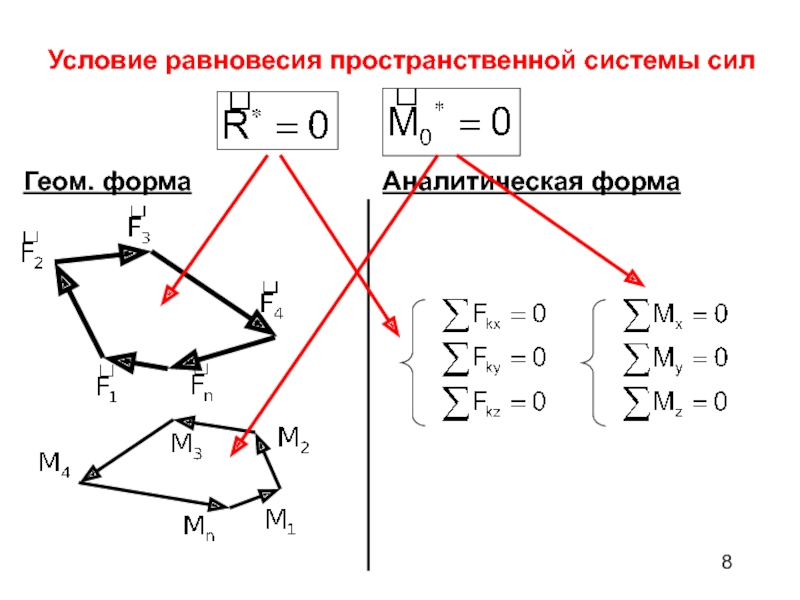
- 8. Условие равновесия пространственной системы силГеом. формаАналитическая форма
- 9. Центр тяжести1. Центр параллельных сил. Его координаты.Рассмотрим
- 10. Определение координат центра параллельных силВыберем систему координат
- 11. Слайд 11
- 12. Координаты центра параллельных сил в векторнойформе В скалярном виде:Статические моменты относительно осей x,y,z:
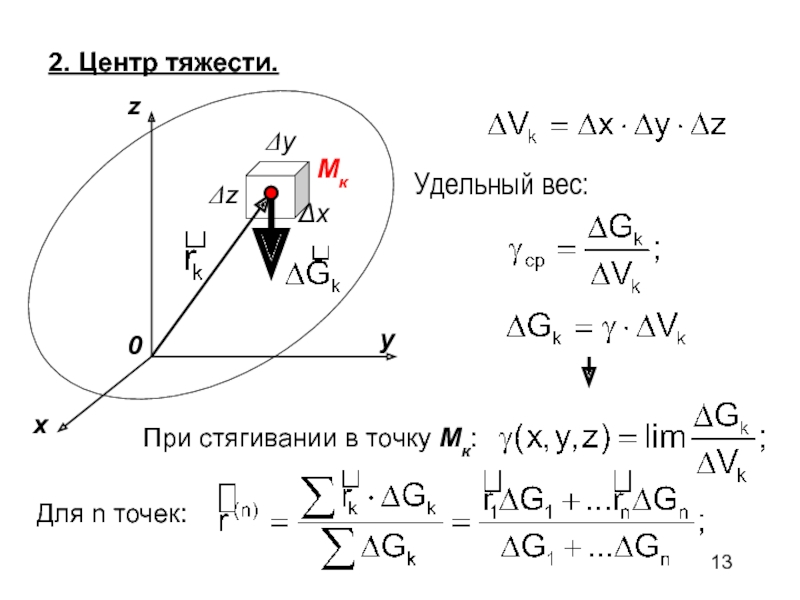
- 13. 2. Центр тяжести.xzy0xyzУдельный вес:МкПри стягивании в точку Мк:Для n точек:
- 14. Объемные телаПлоские телаЛинейные тела
- 15. 3. Методы нахождения центра тяжести
- 16. Слайд 16
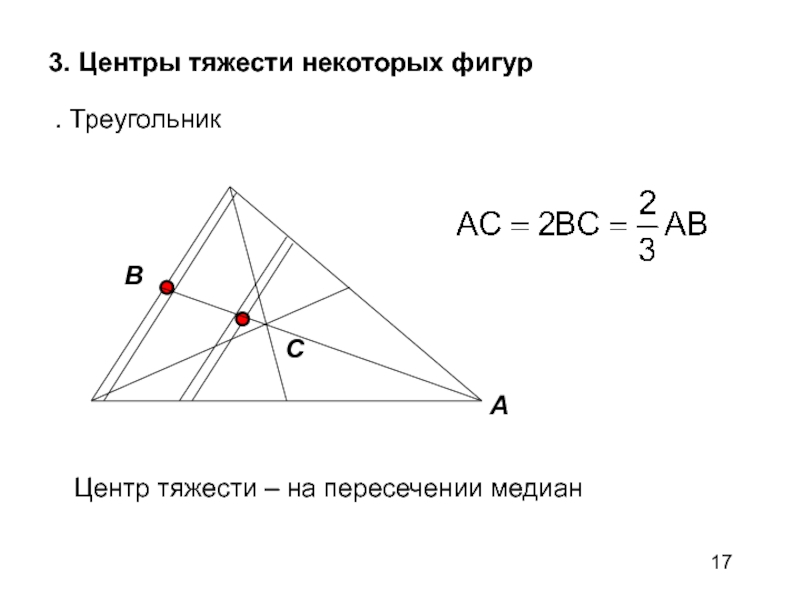
- 17. 3. Центры тяжести некоторых фигур. ТреугольникABCЦентр тяжести – на пересечении медиан
- 18. Пример. При заданных размерах сечения найти координаты
- 19. Координаты центра тяжести.сечения xc, ycxc= A2 xc2
- 20. Трение скольженияЗаконы трения: 1) при действии силы
- 21. Равновесие груза на наклонной плоскости.При постепенном увеличении
- 22. Трение каченияПри действии силы F на ось
- 23. СамостоятельноМещерский И.В. Задачи 2.2, 2.6-2.9, 2.152.16, 2.29-2.31.
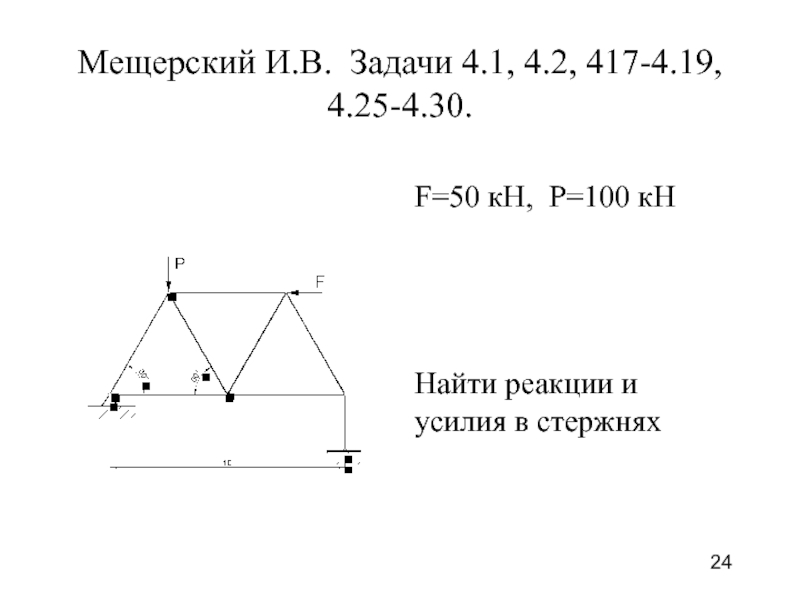
- 24. Мещерский И.В. Задачи 4.1, 4.2, 417-4.19, 4.25-4.30.
- 25. Пример. Определить опорные реакции для консольной балки.Исходные
- 26. Решение1. На балку действуют активные силовые факторы:
- 27. Сумма проекций всех сил на оси X,
- 28. Проверка.Сумма моментов всех сил относительно т. С:∑mС=0:
- 29. Определение внутренних силовых факторов при изгибе балкиВнутренние
- 30. Слайд 30
- 31. Определение внутренних силовых факторов при изгибе балкиВнутренние
- 32. Слайд 32
- 33. Пример. Определить внутренние силовые факторы, построить эпюры
- 34. Участок АС 2. Участок СВ
- 35. Слайд 35
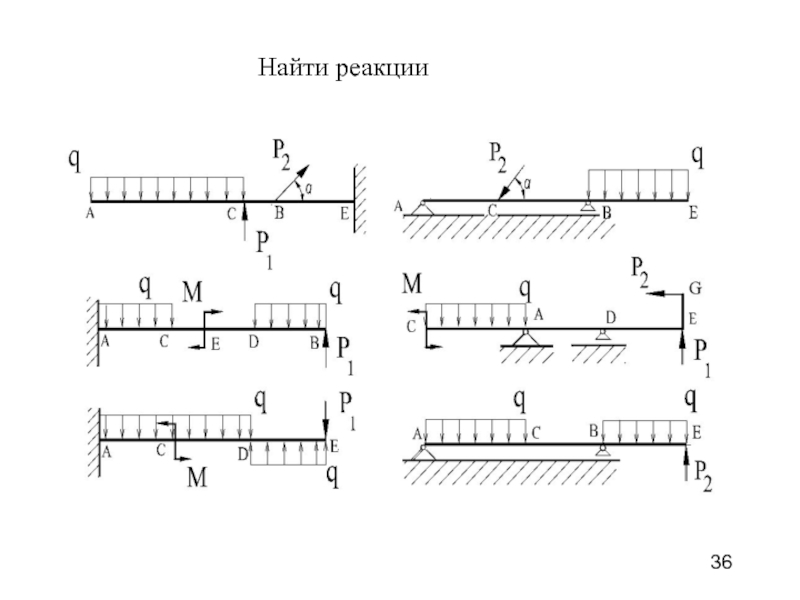
- 36. Найти реакции
- 37. Скачать презентанцию
Слайды и текст этой презентации
Слайд 11. Статически определимые и
неопределимые задачи
Задача считается статически определимой, если
Слайд 3Ферма – конструкция, состоящая из большого числа стержней, соединенных в
точках схода их осей (в узлах).
2. Фермы
Предположения:
1. Внешние силы приложены
в узлах,2. Вес стержней 0,
3. Узлы – идеальные шарниры (нет трения).
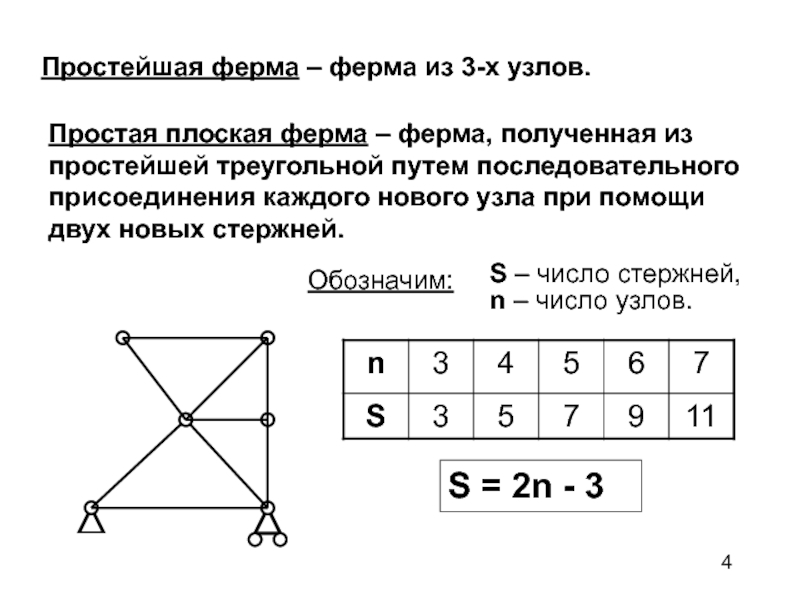
Слайд 4Простейшая ферма – ферма из 3-х узлов.
Простая плоская ферма –
ферма, полученная из простейшей треугольной путем последовательного присоединения каждого нового
узла при помощи двух новых стержней.Обозначим:
S – число стержней,
n – число узлов.
S = 2n - 3
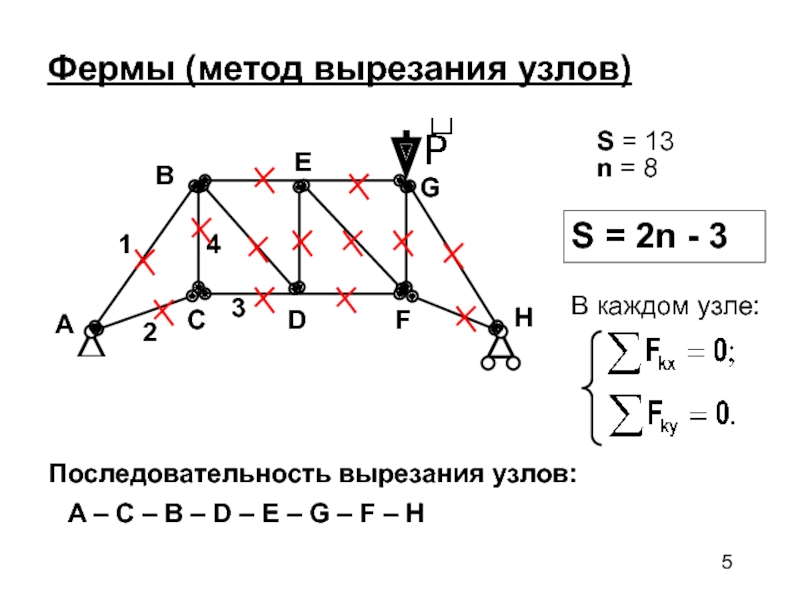
Слайд 5Фермы (метод вырезания узлов)
S = 2n - 3
A
D
C
B
E
F
G
H
S = 13
n
= 8
1
2
3
Последовательность вырезания узлов:
A – C – B – D
– E – G – F – H 4
В каждом узле:
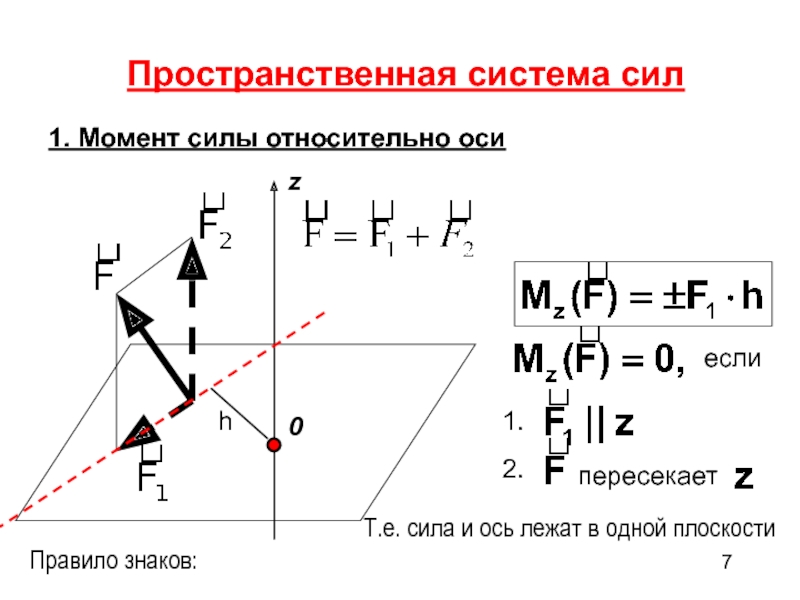
Слайд 7Пространственная система сил
1. Момент силы относительно оси
z
h
0
если
1.
2.
пересекает
Т.е. сила и ось
лежат в одной плоскости
Правило знаков:
Слайд 9Центр тяжести
1. Центр параллельных сил. Его координаты.
Рассмотрим такую систему параллельных
сил, которая приводится к равнодействующей:
Определим, что происходит с равнодействующей при
повороте системы сил вокруг оси, перпендикулярной линиям действия сил. Точка, вокруг которой осуществляется этот поворот, называется центром параллельных сил (это точка приложения равнодействующей параллельных сил).Слайд 10Определение координат центра
параллельных сил
Выберем систему координат таким образом, чтобы
ось Z была параллельна силам. Для определения координаты центра параллельных
сил по оси X воспользуемся теоремой Вариньона о равенстве момента равнодействующей сумме моментов составляющих:
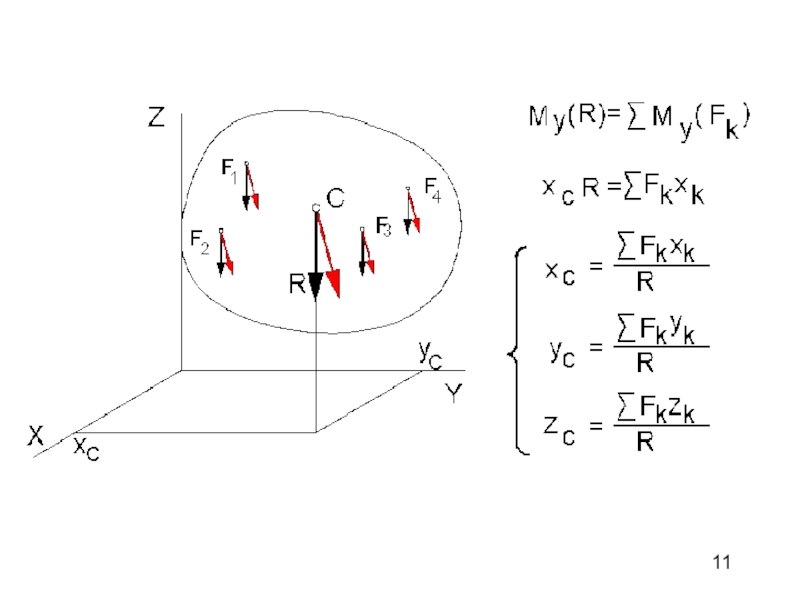
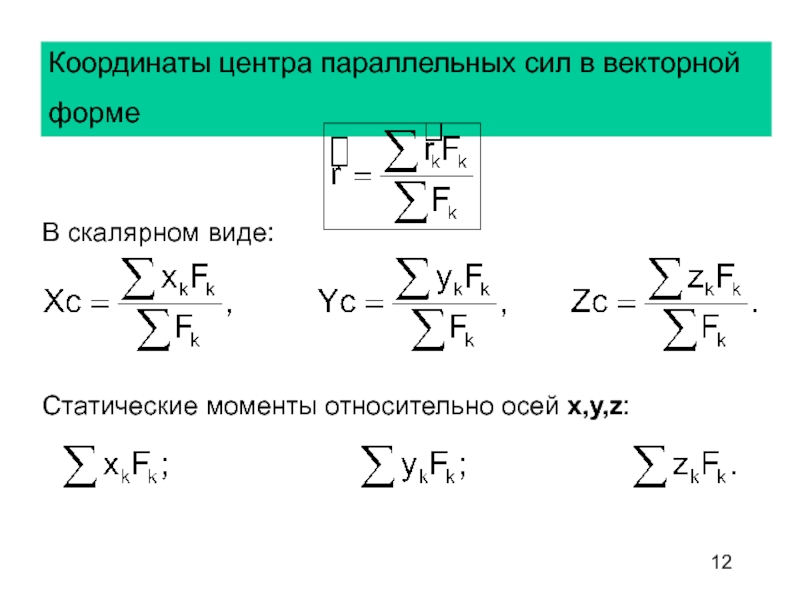
Слайд 12Координаты центра параллельных сил в векторной
форме
В скалярном виде:
Статические моменты
относительно осей x,y,z:
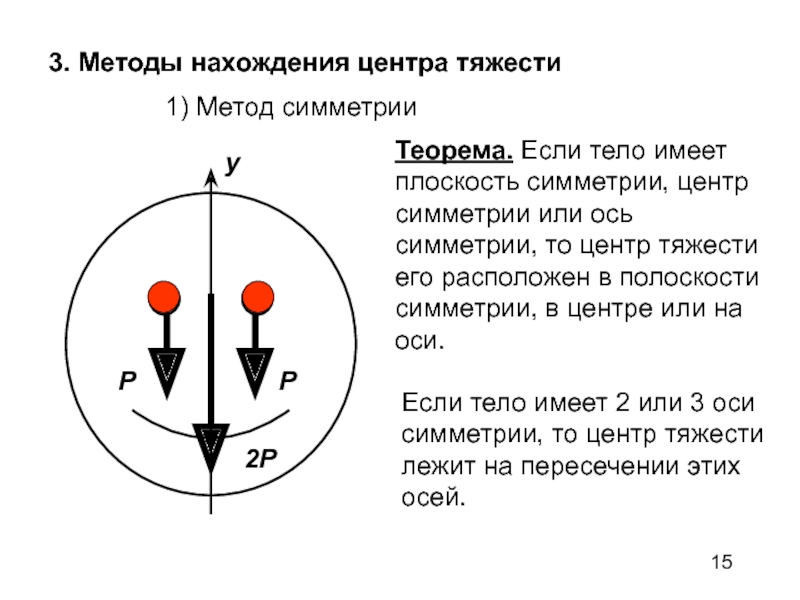
Слайд 153. Методы нахождения центра тяжести
1) Метод симметрии
Теорема. Если тело имеет плоскость симметрии,
центр симметрии или ось симметрии, то центр тяжести его расположен в полоскости симметрии, в центре или на оси.y
Р
Р
2Р
Если тело имеет 2 или 3 оси симметрии, то центр тяжести лежит на пересечении этих осей.
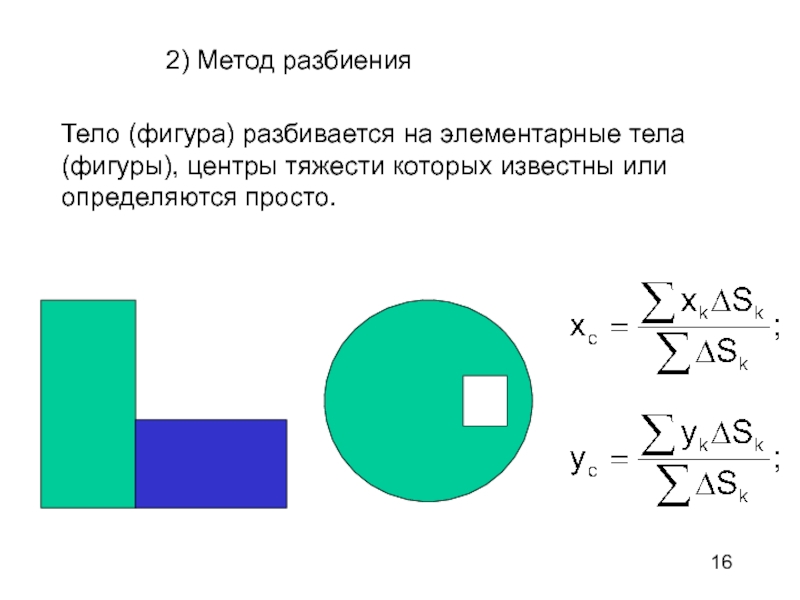
Слайд 16 2) Метод
разбиения
Тело (фигура) разбивается на элементарные тела (фигуры), центры тяжести которых
известны или определяются просто.Слайд 18Пример. При заданных размерах сечения найти координаты центра тяжести. сечения
xc, yc
Площади 1 и 2 фигуры
А1= cd
A2=abКоординаты центров тяжести. 1 и 2 фигуры
xc1=0, yc1=OA=(b+c)/2,
xc2= OB=(a-d)/2, yc2=0.
Слайд 19
Координаты центра тяжести.сечения xc, yc
xc= A2 xc2 / (A1 +
A2) = ab (a-d)/ 2 ( cd+ ab )
yc= A1
yc1 / (A1 + A2) = cd (b+c) / 2( cd+ ab )Слайд 20Трение скольжения
Законы трения: 1) при действии силы F,параллельной поверхности, на
которой находится тело, возникает сила трения, препятствующая перемещению;
2) сила
трения изменяется от нуля до максимального значения равного произведению статического коэффициента трения f на силу нормального давления Fm=f0N 3) при движении сила трения препятствует движению и равна произведению динамического коэффициента трения f на силу нормального давления F=fN
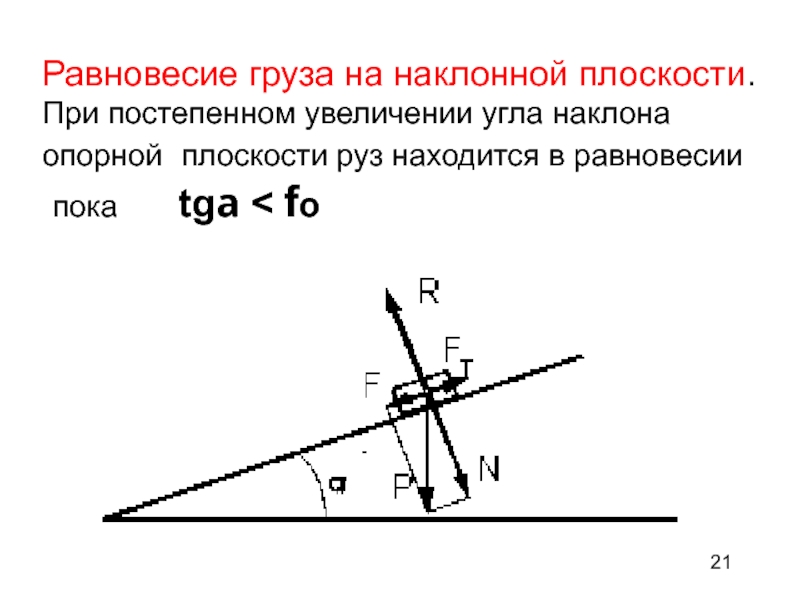
Слайд 21Равновесие груза на наклонной плоскости.
При постепенном увеличении угла наклона
опорной
плоскости руз находится в равновесии
пока tga
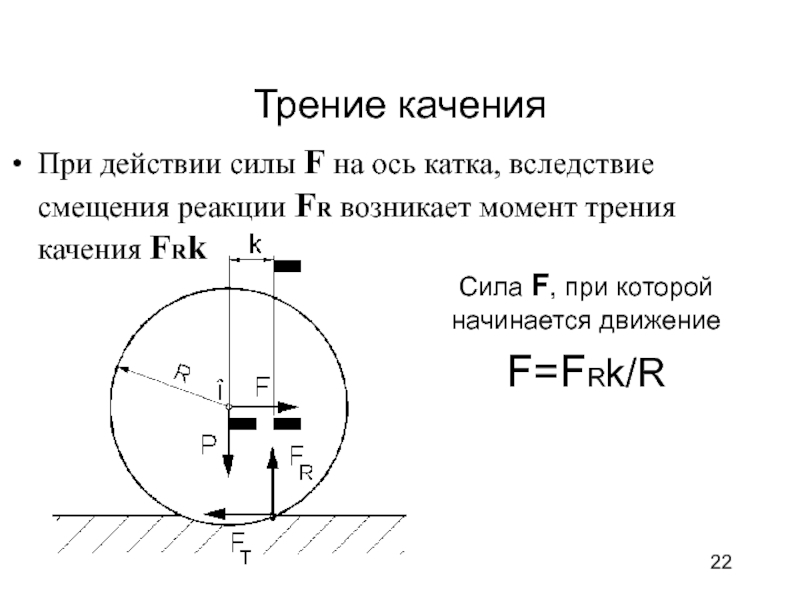
< foСлайд 22Трение качения
При действии силы F на ось катка, вследствие смещения
реакции FR возникает момент трения качения FRk
Сила F, при которой
начинается движениеF=FRk/R
Слайд 23Самостоятельно
Мещерский И.В. Задачи 2.2, 2.6-2.9, 2.15
2.16, 2.29-2.31.
F=50 кН, a =30
Найти Fx, Fy, Mo
a
Y
F
F
F
F
8
x
y
6
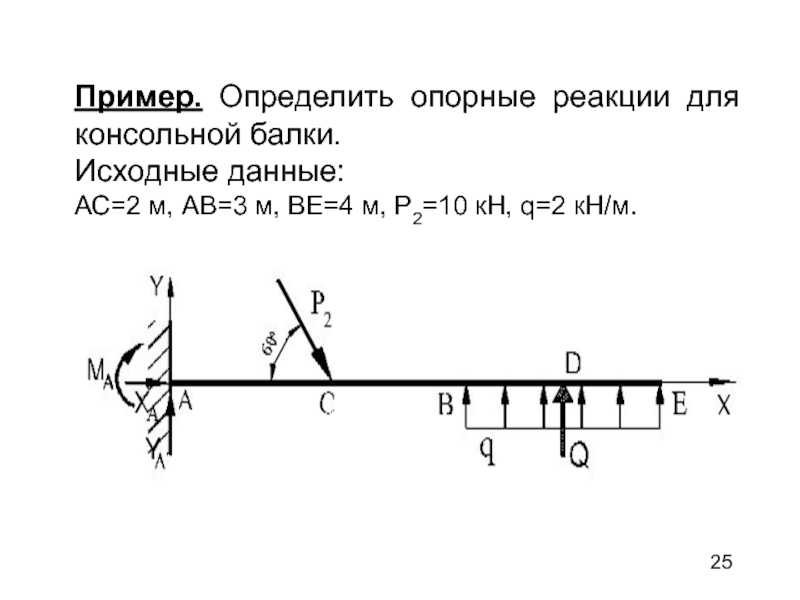
Слайд 25Пример. Определить опорные реакции для консольной балки.
Исходные данные:
АС=2 м, АВ=3
м, ВЕ=4 м, Р2=10 кН, q=2 кН/м.
Слайд 26Решение
1. На балку действуют активные силовые факторы: сосредоточенная сила Р2
и равномерно распределенная нагрузка интенсивностью q.
2. В сечении А опора
защемления, в которой ограничены три степени свободы. При мысленном освобождении их воздействие заменяем реакциями XA, YA, и MA. Система является геометрически неизменяемой и статически определимой. 3. Запишем три условия равновесия для плоской системы сил, действующих на балку. Равномерно распределенную нагрузку на участке ВЕ заменим равнодействующей Q=q ВЕ, приложенной в т. D (BD=DE).Слайд 27Сумма проекций всех сил на оси X, Y:
∑FX=0:
XA +Р2 cos 60=0,
∑FY=0: YA −P2 sin60 + Q
=0.Сумма моментов всех сил относительно т. А:
∑mA=0: −MA − P2 sin60 AC +Q (AB+ BD).
Решим полученную систему алгебраических уравнений относительно неизвестных XA, YA, и MA.
XA= −5 кН; YA = 0,66 кН; MA= 22,68 кНм.
Отрицательное значение реакции XA означает, что её действительное направление противоположно выбранному.
Слайд 28
Проверка.
Сумма моментов всех сил относительно т. С:
∑mС=0: −MA +
q BE (СB+ BE/2) − YA АС=
−22,68 +2*4*3−0,66*2= 0.
Проверка
показала, что реакции XA, YA, MA определены правильно.Ответ: XA= −5 кН; YA = 0,66 кН; MA= 22,68 кНм.
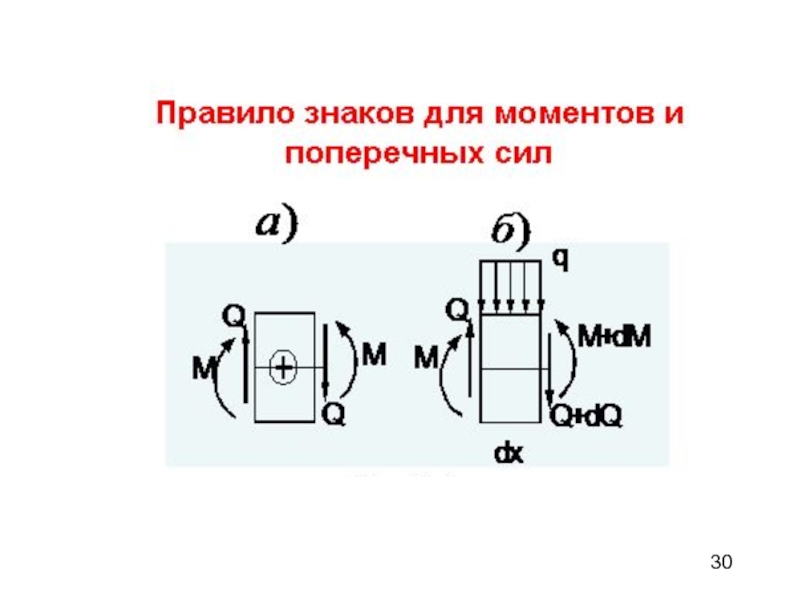
Слайд 29Определение внутренних силовых
факторов при изгибе балки
Внутренние силовые факторы выявляем
методом сечений. Воздействие отсеченной части заменяем нормальной N и поперечной
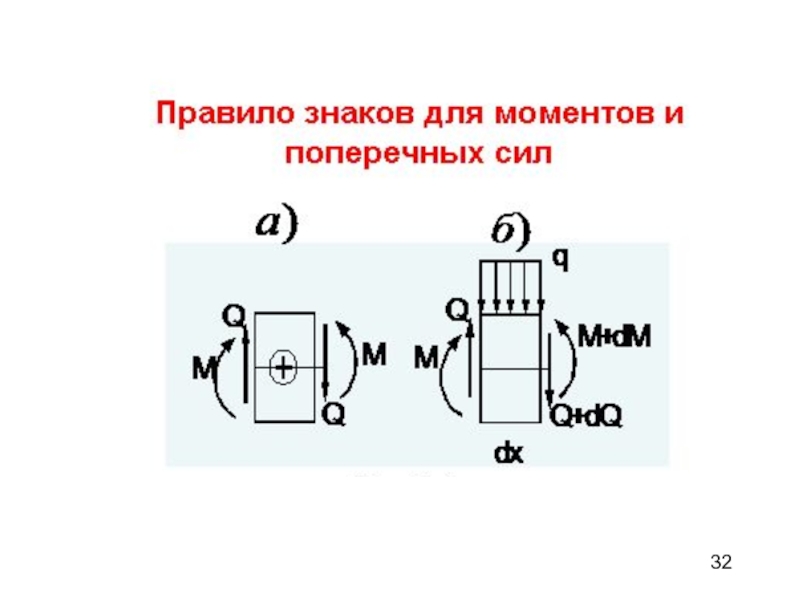
Q силами и изгибающим моментом MZ относительно оси, проходящей через центр тяжести сечения.Слайд 31Определение внутренних силовых
факторов при изгибе балки
Внутренние силовые факторы выявляем
методом сечений. Воздействие отсеченной части заменяем нормальной N и поперечной
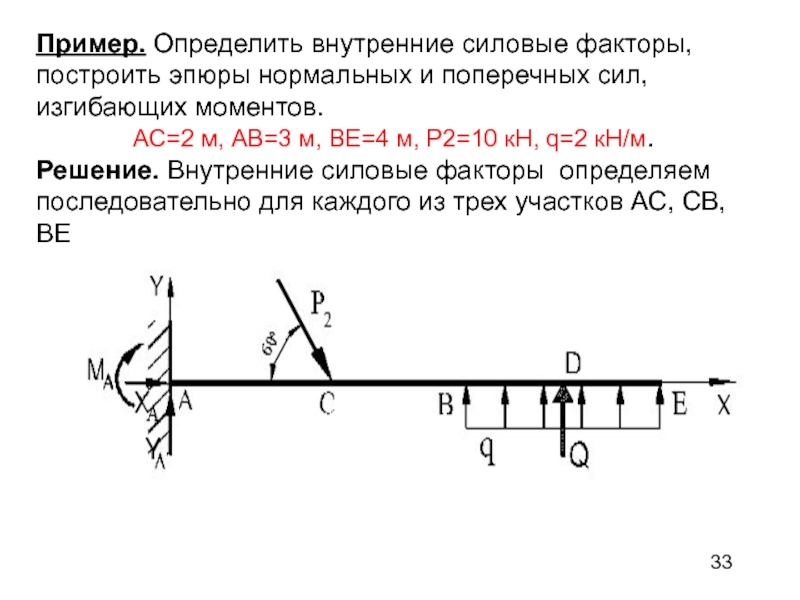
Q силами и изгибающим моментом MZ относительно оси, проходящей через центр тяжести сечения.Слайд 33Пример. Определить внутренние силовые факторы, построить эпюры нормальных и поперечных
сил, изгибающих моментов.
АС=2 м, АВ=3 м, ВЕ=4 м, Р2=10 кН,
q=2 кН/м.Решение. Внутренние силовые факторы определяем последовательно для каждого из трех участков АС, СВ, ВЕ
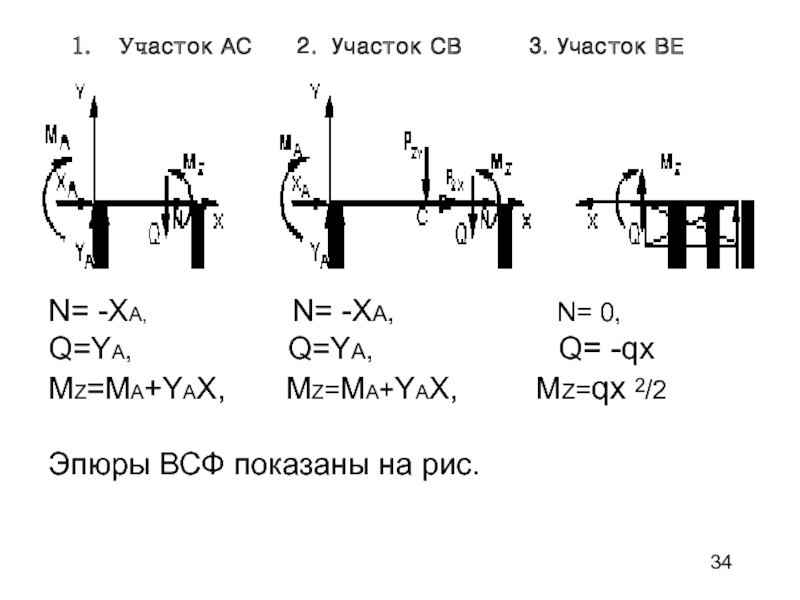
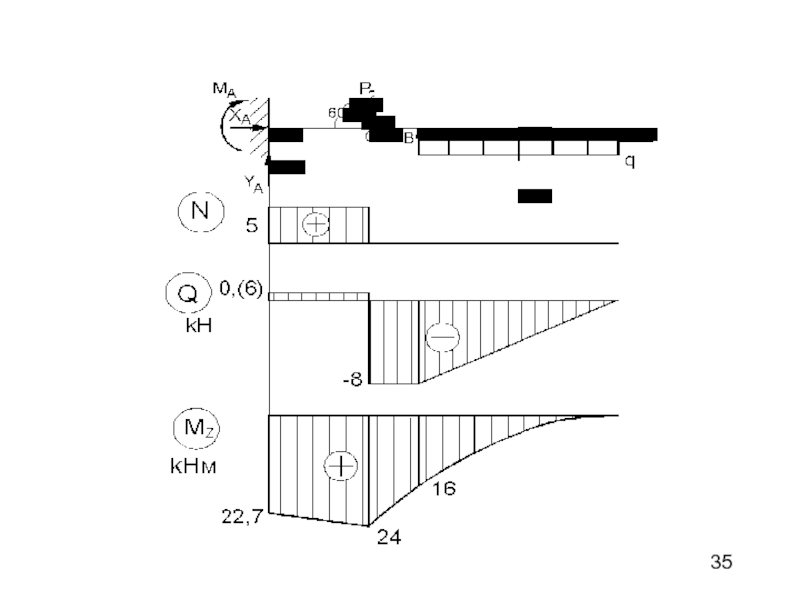
Слайд 34Участок АС 2. Участок СВ
3. Участок ВЕ
N= -XA,
N= -XA, N= 0,Q=YA, Q=YA, Q= -qx
MZ=MA+YAX, MZ=MA+YAX, MZ=qx /2
Эпюры ВСФ показаны на рис.
2





















![[SP]IT. Russia](/img/thumbs/6a9e7165525d9ca0b026496ad1b87ab7-800x.jpg)










