1.1 Цепи постоянного тока

квадрата силы тока,
сопротивления проводника,
времени.
Работа тока A= UIt
Количество теплоты

Закон Ома

нагрузки от нуля до бесконечности
=>
Ток через нагрузку растет от

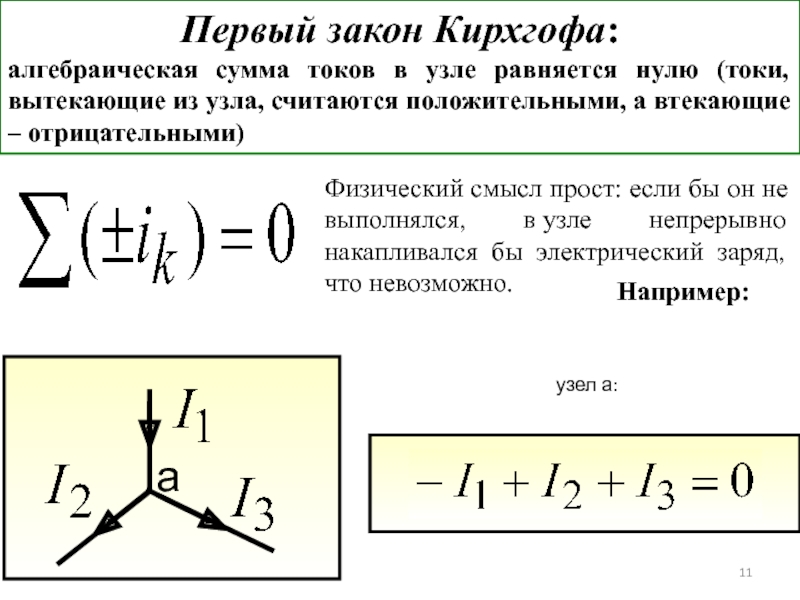
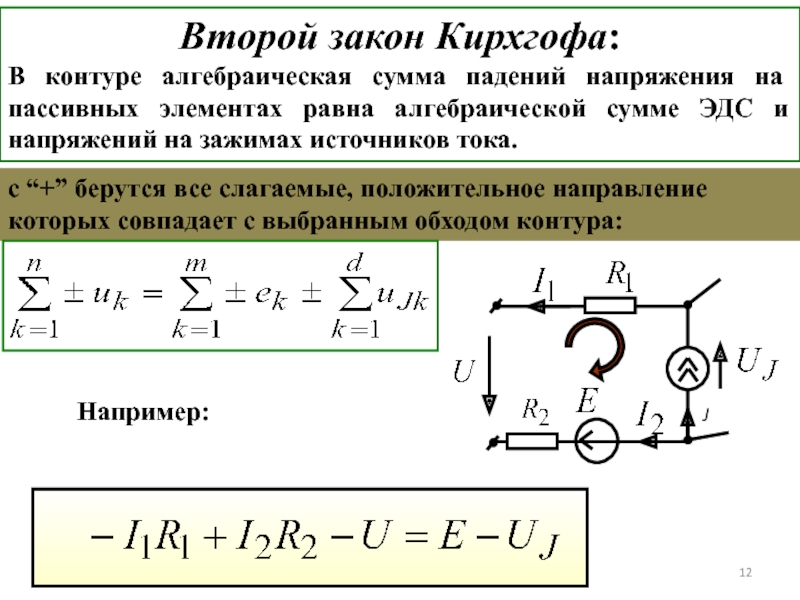
Идеальные источники НАПРЯЖЕНИЯ (ЭДС) и ТОКА

Применяются для расчетов в электротехнике

ИСТОЧНИК ТОКА дает неизменный ток при любой нагрузке
При росте сопротивления нагрузки от нуля до бесконечности =>
Напряжение на нагрузке растет от нуля до бесконечности.

Внутренняя ПРОВОДИМОСТЬ источника тока равна нулю.

У источника напряжения напряжение не зависит от нагрузки,
У источника тока - ток.

ток
§2. Основные законы электротехники

под общим напряжением

АН,
член-корреспондент Петербургской АН.

(токи, вытекающие из узла, считаются положительными, а втекающие – отрицательными)
Физический

Например:

пассивных элементах равна алгебраической сумме ЭДС и напряжений на зажимах

с “+” берутся все слагаемые, положительное направление которых совпадает с выбранным обходом контура:

Например:

позволяет определить все токи и напряжения в рассматриваемой цепи
1 шаг

системы:

равна сумме потребляемых мощностей во всех пассивных элементах
рассматриваемой цепи

Кирхгофа и позволяет упростить систему уравнений
Контурный ток – это ток,

3.1.Метод контурных токов

Общая форма записи

этого контура.
2. К этому произведению дописываются произведения всех соседних контурных

ток будет равен току источника тока, через источник тока должен

Порядок расчета

Обозначаются токи ветвей
Выбираются контурные токи
Составляется система уравнений по алгоритму
Находятся контурные токи
Через контурные токи находятся реальные токи схемы

(например, узел 1 и узел 2).

2:
– алгебраическая сумма отношений ЭДС ветвей к сопротивлениям этих

– алгебраическая сумма токов источников тока (с «+», если его направление не совпадает с U12 );

Порядок расчета

– сумма проводимостей всех ветвей, соединяющих узлы 1 и 2.

направление тока Ik в k-ой ветви совпадает с направлением U12

Rk – сопротивление k-ой ветви.