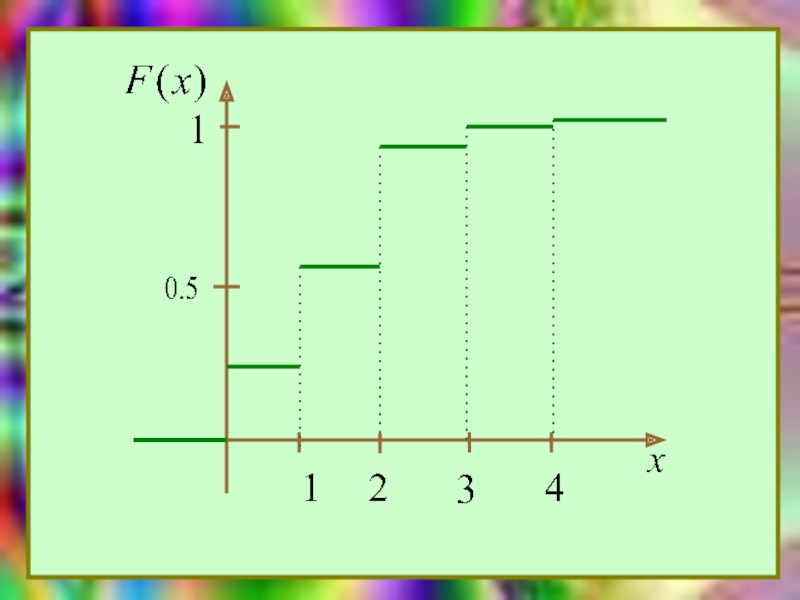
Она может быть определена как для дискретных, так и для
непрерывных случайных величин.Введем новую характеристику случайных величин - функцию распределения и рассмотрим ее свойства.
Рассмотрим вероятность того, что СВ Х примет значение, меньшее, чем х, т.е. Р(Х<х),