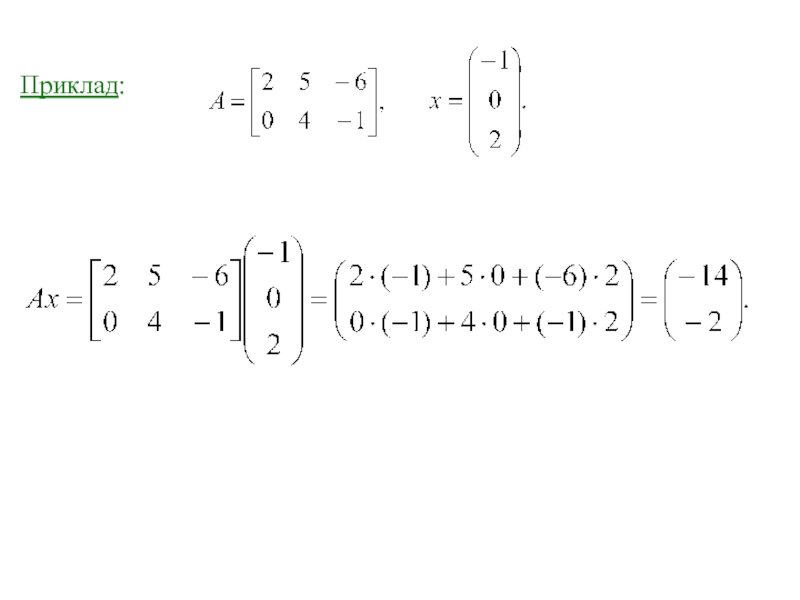МАТРИЦІ ТА ВИЗНАЧНИКИ 1. Матриці та їх властивості 2. Лінійні операції над

матрицями 3. Визначники та їх властивості

розміру mn називається сукупність чисел, розташованих у вигляді таблиці з

m рядків і n стовпчиків:

Числа, що складають матрицю, називаються елементами матриці. Якщо m≠n, то матриця називається прямокутною. Якщо m=n, то матриця называється квадратною порядку n.

Приклад:

размера 33

складається з одного рядка – вектор-рядок.
Матриця розміру m1 виду
,

що складається з одного стовпця

У випадку квадратної матриці

елементи a11, a22,…ann утворюють головну діагональ, а елементи an1, an-1 2,…a1n – побічну діагональ матриці.

нульовою матрицею.
називається одиничною.
Матриця
1.2 Лінійні операції над

матрицями

1. Порівняння
А=В, якщо у них елементи, що розташовані на відповідних місцях, рівні.

Для того, чтоб додать дві матриці A і

B (одинакової розмірності) необхідно додать їх відповідні елементи.

Приклад: Нехай

Тоді

Для того, чтобы знайти різницю матриць А і В (одинакової розмірності) необхідно з кожного елемента матриці А відняти відповідний елемент матриці В.

число R необхідно кажен элемент матриці помножить на число .
Приклад:

Нехай

тоді

х необхідно, щоб число стовпців n матриці А дорівнювало числу

елементів вектор-стовпчика х. Тоді добуток матриці А на вектор-стовпець х позначається Ах і дорівнює

.

стовців матриці а дорівнює числу рядків матриці В.

Добутком матриці А на матрицю В називається mk матриця С з елементами сij, що дорівнюють сумі добутків елементів i-го рядка матриці А на відповідні елементи j-го стовпця матриці В, сij=ai1b1j+ai2b2j+…+ainbnj,

i=1..m, j=1..k.

5. Множення двох матриць

з даной матриці А шляхом заміни рядків на стовпчики, і

навпаки, називається транспонованою.

Приклад:

квадратних матриць.
Визначником n-го порядку матриці А називається алгебраїчна сума всіляких

добутків елементів, взятих точно по одному з кожного рядка і кожного стовпчика матриці А. Знак кожного доданка визначається спеціальним правилом.

Визначник n-го порядку містить n! членів.

= a11a22- a12a21 – визначник другого порядку.

Приклад:

головної діагоналі і елементів, що знаходяться в вершинах двох рівнобедрених

трикутників, основи яких паралельні головній діагоналі. Три його від'ємних члена є добутком елементів побічної діагоналі і елементів, що знаходяться в вершинах двох рівнобедрених трикутників, основи яких паралельні побічної діагоналі.

a11a22a33+a12a23a31+ a13a21a32- a13a22a31-a11a23a32-

-a12a21a33 – визначник третього порядку.

«+»

«-»

визначнику транспонованою матриці,
2. Якщо всі елементи деякого рядка матриці

А дорівнюють 0, то визначник дорівнює 0.
3. Загальний (спільний) множник всіх елементів рядка визначника можна винести за знак цього визначника.
4. Якщо у визначнику поміняти місцями два рядки, то він змінить знак на протилежний.
5. Якщо визначник має два рівні рядки, то він дорівнює 0.
6. Якщо елементи двох рядків визначника пропорційні, то визначник дорівнює 0.

додати відповідні елементи іншого рядка, помножені на одне і те

ж число k.

Мінором Мij елемента aij називається визначник (n-1) порядку, отриманний викресленням з визначника n-го порядку елементів i –го рядка та j-го стовпця, i, j=1..n.
Приклад:

Алгебраїчним доповненням елемента aij називаєтьчя число

Aij=(-1)i+j Мij.

– мінор
елемента а23.

A23=(-1)2+3 М23=(-1)(-6)=6.

добутків елементів будь-якого його рядка на відповідні алгебраїчні доповнення елементів

цього рядка.
Формула Лапласа:

Приклад: обчислити визначник

а) за правилом трикутника:

:
A =a31A31+a32A32+a33A33,