Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
14.02.2019 К л а с с н а я р а б о т а. Задачи на построение
Содержание
- 1. 14.02.2019 К л а с с н а я р а б о т а. Задачи на построение
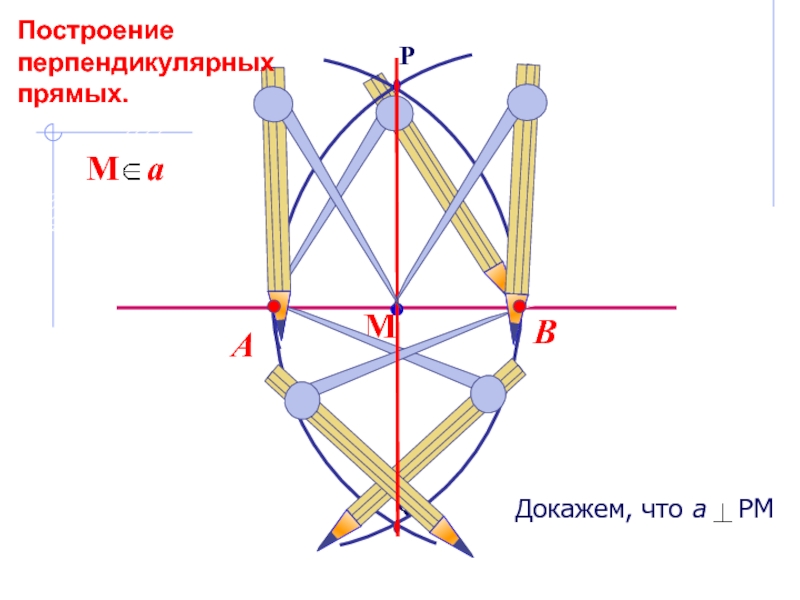
- 2. ВАПостроение перпендикулярных прямых.
- 3. МaДокажем, что а РМАМ=МВ, как радиусы
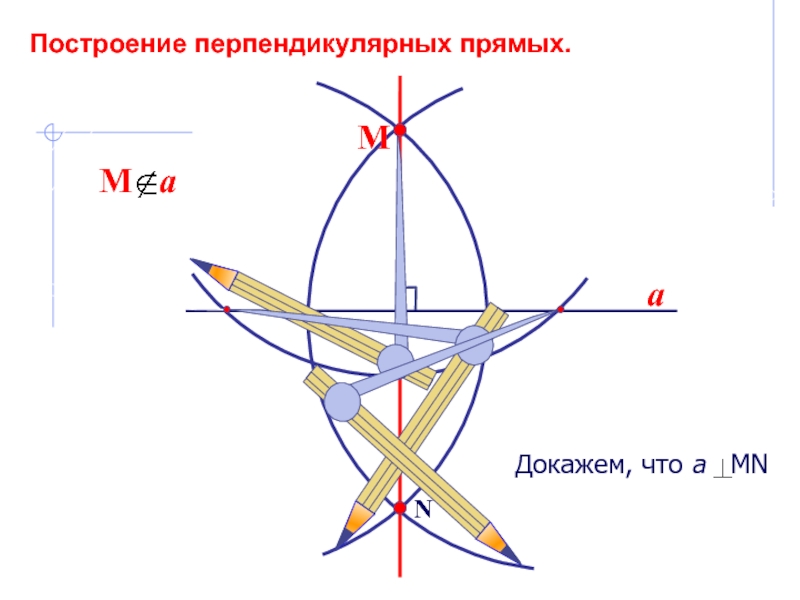
- 4. aNМПостроение перпендикулярных прямых.
- 5. aNBACМПосмотрим на расположение циркулей.АМ=АN=MB=BN, как равные радиусы. МN-общая сторона. MВN= MAN, по трем сторонам
- 6. Докажем, что О – середина отрезка АВ.Построение середины отрезка
- 7. ВАТреугольник АРВ р/б.Отрезок РО является биссектрисой, а
- 8. п. 22-23, вопросы 20 – 21 (устно, стр.50). Решить задачу № 154. Домашнее задание
- 9. Скачать презентанцию
ВАПостроение перпендикулярных прямых.
Слайды и текст этой презентации
Слайд 3М
a
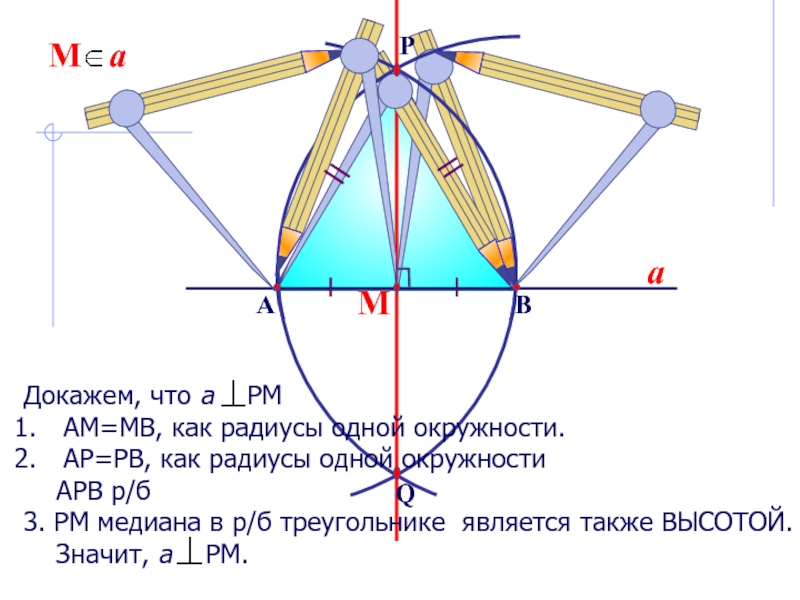
Докажем, что а РМ
АМ=МВ, как радиусы одной окружности.
АР=РВ, как
радиусы одной окружности
АРВ р/б
3. РМ медиана в р/б
треугольнике является также ВЫСОТОЙ. Значит, а РМ.
Слайд 5a
N
B
A
C
М
Посмотрим
на расположение
циркулей.
АМ=АN=MB=BN,
как равные радиусы.
МN-общая сторона.
MВN= MAN,
по трем сторонам
Слайд 7В
А
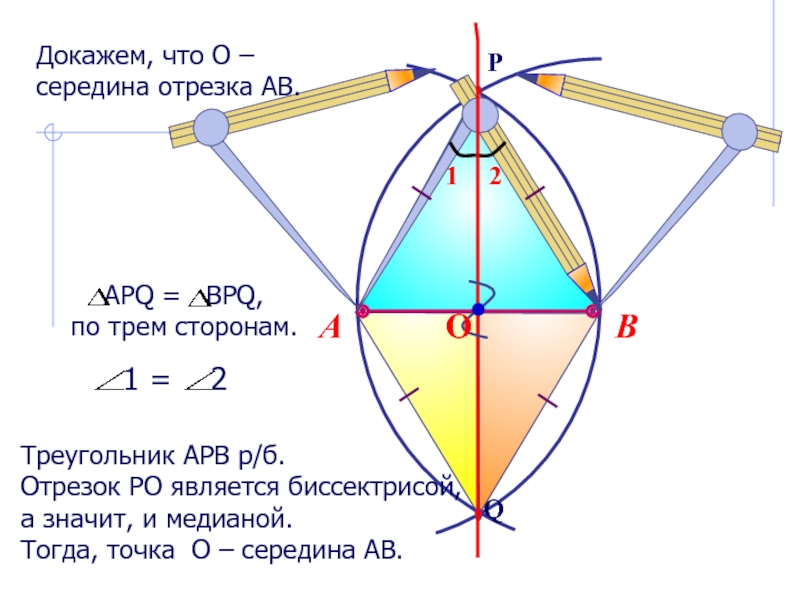
Треугольник АРВ р/б.
Отрезок РО является биссектрисой,
а значит, и медианой.
Тогда, точка О – середина АВ.
Докажем, что О –
середина отрезка АВ.