Слайд 1Лекция № 3
Основні логічні операції над двійковими числами
(основы алгебры логики)
Слайд 2логические основы
Математическим аппаратом, применяемым при анализе и синтезе ЛЭУ, является
алгебра логики, разработанная в середине Х1Х века английским математиком Дж.
Булем, и поэтому часто называемая Булевой алгеброй (БА).
БА оперирует с двоичными (логическими) переменными, принимающими одно из двух значений: логический нуль или логическая единица.
Слайд 3План лекции
1.Логические функции переменных. Таблицы истинности.
2.Элементарные логические функции двух
переменных
3Логические теоремы.
4. Формы представления логических функций. Методы минимизации уравнений.
Карты Карно.
Слайд 5
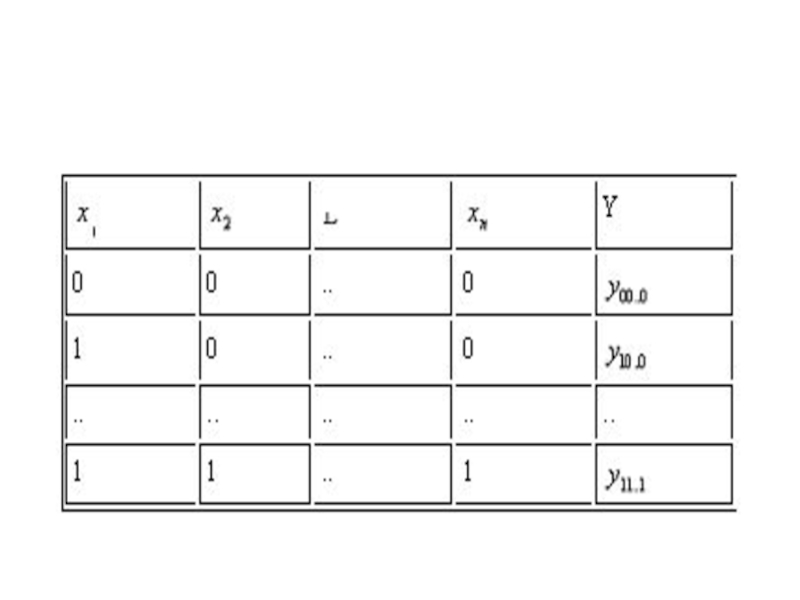
Функция двоичных переменных также равная одному из двух значений (нулю
или единице) - называется переключательной (логической) функцией (ПФ).
Логические функции обозначаются
прописными буквами F или Y, а двоичные переменные - А, В, С, D, E, ... или строчной буквой икс с индексом, например, x1, х2, х3 ... .
ПФ может быть выражена (задана):
словесно;
алгебраическим (булевым) выражением;
таблицей истинности;
(картой Карно).
Переключательные функции одной переменной (n=1)
Если n=1, то число наборов N=2*1=2,
Слайд 6.Логические функции переменных. Таблицы истинности.
Слайд 7
Логические функции оперируют логическими переменными, т.е. переменными, принимающими только два
значения:
ИСТИНА и ЛОЖЬ (на математическом языке - 0 и
1).
В общем случае логические выражения являются функциями логических переменных А,В,С, каждая из которых может иметь значение 0или1
Результат логической функции может принимать тоже только эти два значения.
Для представления логических функций используют аппарат логических уравнений и таблиц истинности.
F8=АВ=А*В
F14=АВ=А+В
Слайд 8Таблица истинности
таблица в которой каждой комбинации входных логических переменных
ставится в соответствие требуемое значение данной логической функции.
Слайд 10
Логические функции могут быть одной, двух и более логических переменных.
Если имеется К логических переменных то они образуют 2 в
степени К возможных логических наборов из 0 и 1,при к=1
А=0 иА=1
приК=2
АВ=00,01,10,11(4)
Для каждого набора переменных логическая функция F может принимать значение 0 или 1, поэтому для К переменных можно образовывать 2*2*к различных логических функций
Слайд 11
А,В,С……… - логические переменные
Количество наборов логических наборов переменных
2*к
Пример: к=1
к-во наборов 2
А,В к=2 4
А,В,С к=3 8
Слайд 12
Для каждого набора переменных логическая функция F может принимать значение
0 или 1, поэтому для К переменных можно образовывать 2*2*к
различных логических функций
Пример:
А к=1 F=4
A,B, k=2 F=16
A,B,C k=3 F=256
Слайд 13Таблица полного набора логических функций для двух переменных
Слайд 17
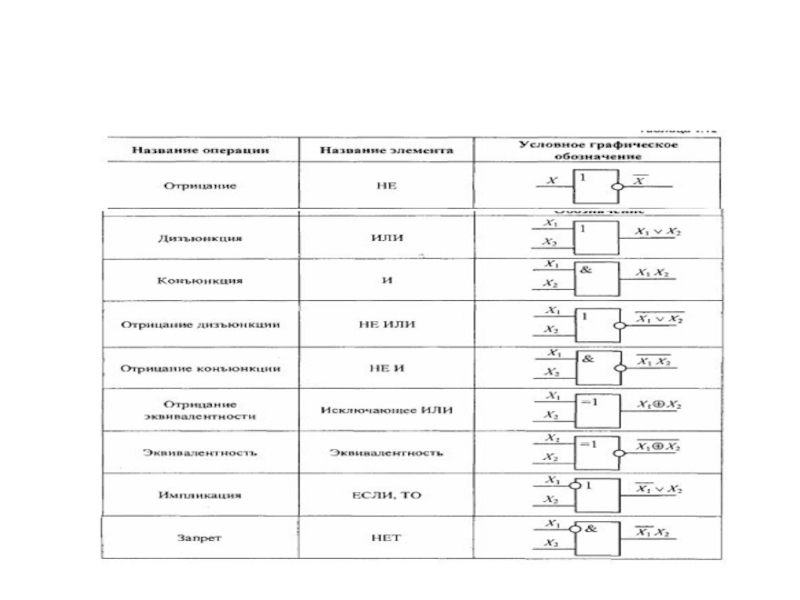
Отметим из этих шестнадцати функций 2-х переменных наиболее часто использующиеся:
F0
– константа нуля;
F15 – константа единицы;
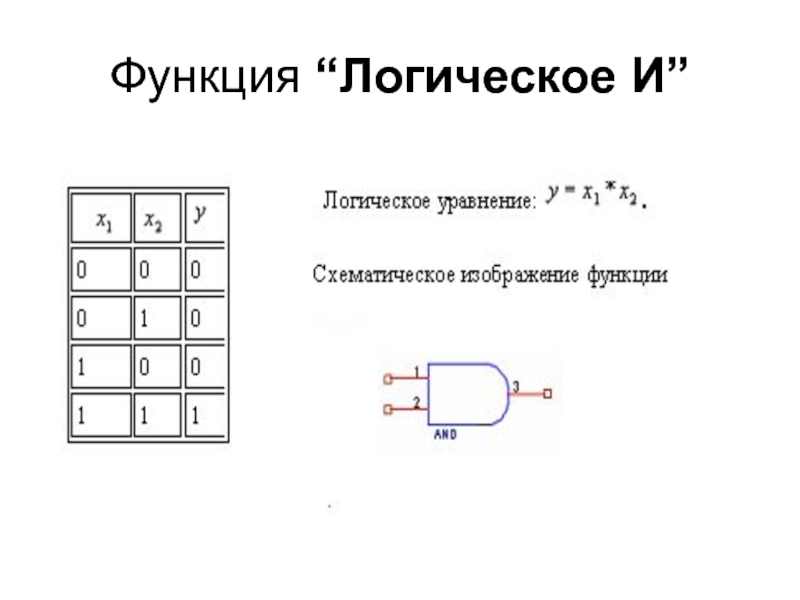
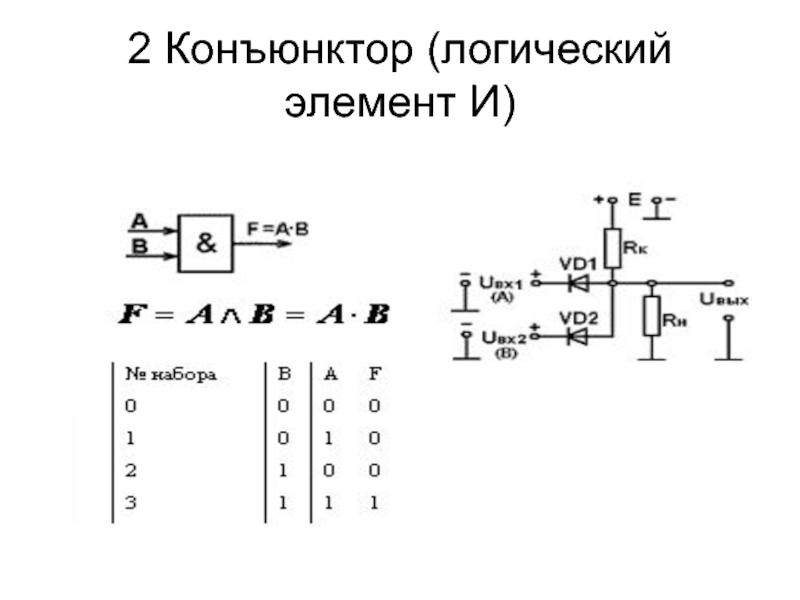
F8=АВ=А*В – конъюнкция (логическое умножение
(логическое “И”));
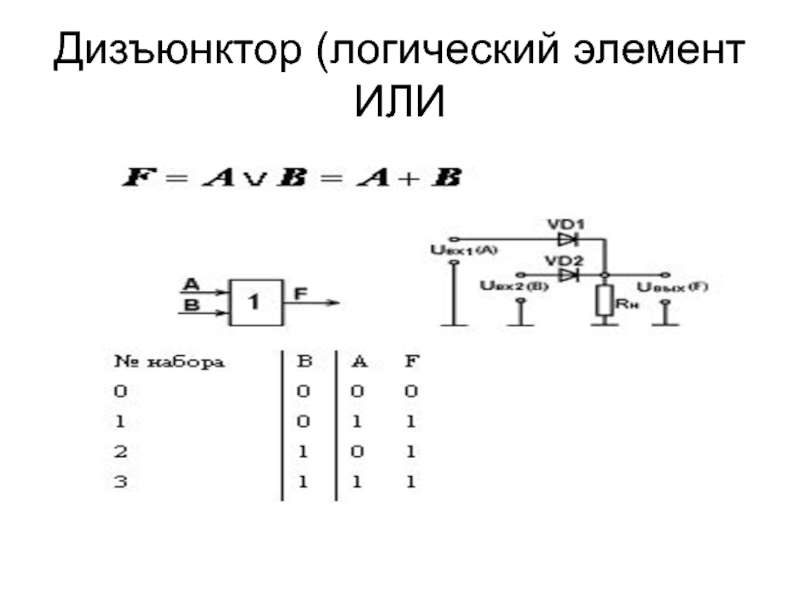
F14=АВ=А+В – дизъюнкция (логическое сложение (логическое “ИЛИ”));
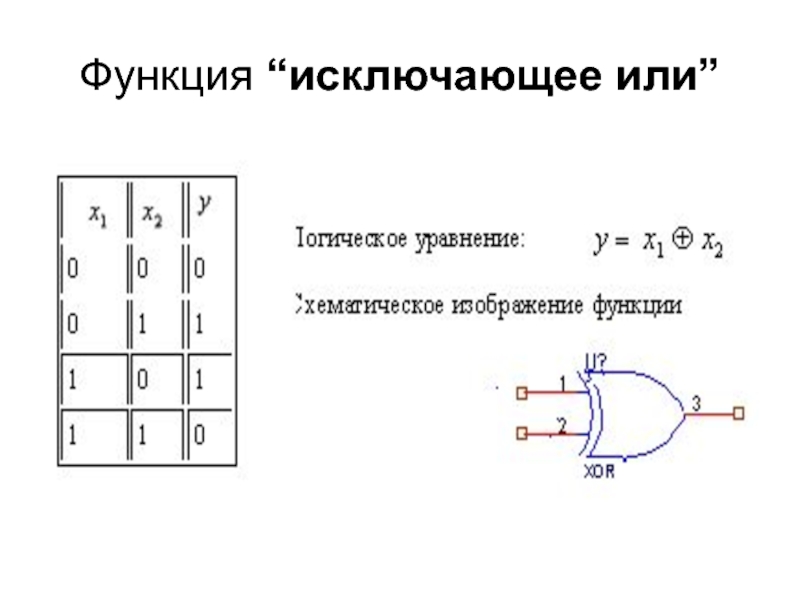
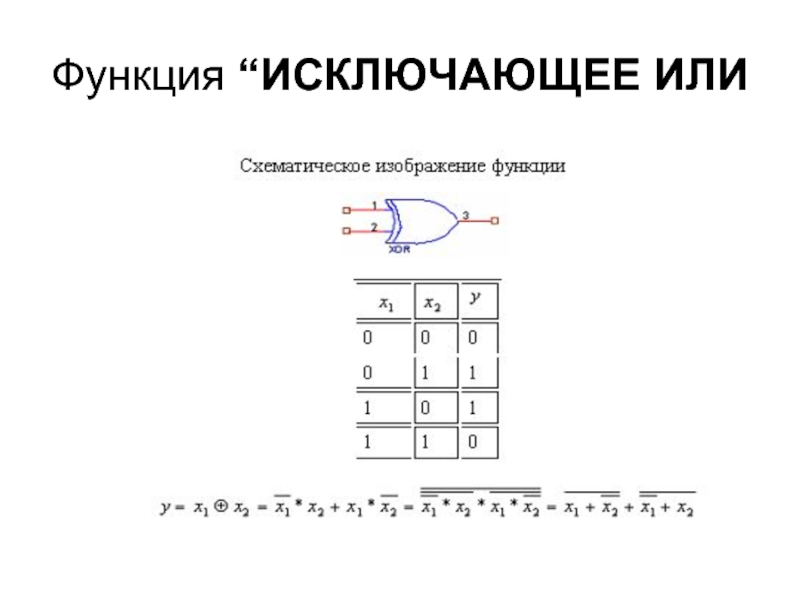
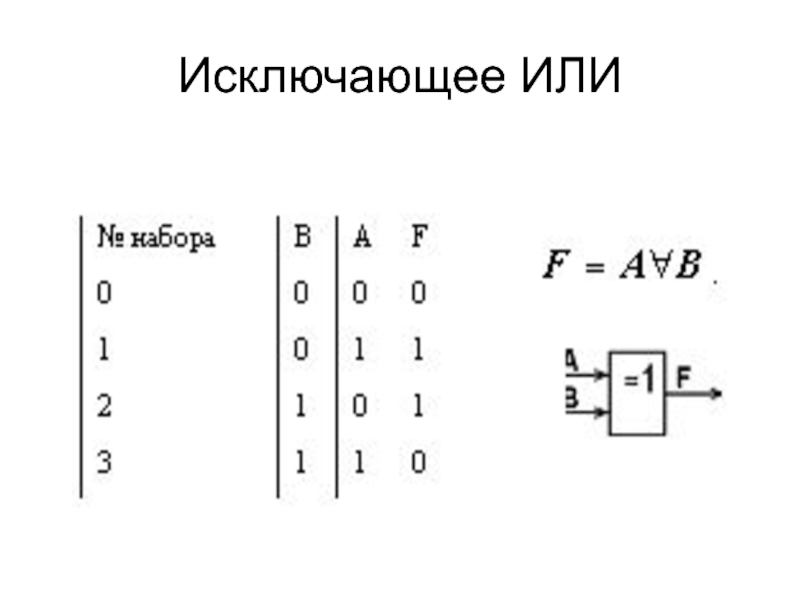
F6= – исключающее ИЛИ (сумма по модулю два, неравнозначность, неэквивалентность);
– равнозначность (эквивалентность);
– ИЛИ-НЕ;
– И - НЕ.
Слайд 18.Элементарные логические функции двух переменных
Слайд 29Основные законы и теоремы булевой алгебры
Переместительный (свойство коммутативности): А+В=В+А; А*В=В*А.
Сочетательный
(свойство ассоциативности): (А+В)+С=А+(В+С); (А*В)*С=А*(В*С).
Распределительный (свойство дистрибутивности): А*(В+С)=А*В+А*С; А+В*С=(А+В)*(А+С).
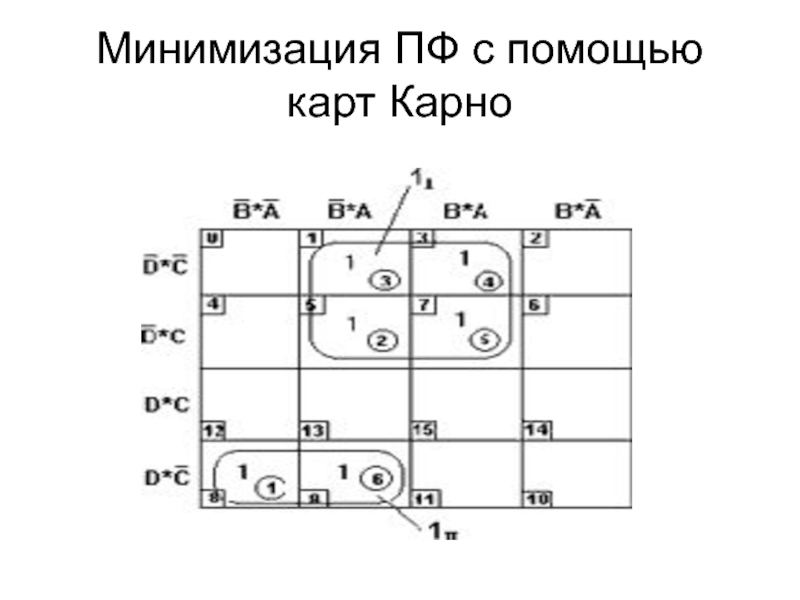
Слайд 32Минимизация ПФ с помощью карт Карно
Слайд 33
Каждая клетка в картах Карно соответствует определенному набору переменных.
Соседние
клетки соответствуют наборам, отличающимся значением одной из переменных.
Каждая строка
и столбец обозначаются значением конкретной переменной или комбинацией (произведением) переменных в прямой или инверсной форме.
Слайд 34
Клетки, помеченные переменными в прямой форме, соответствуют наборам, где эти
переменные принимают единичные значения, а клетки, обозначенные переменными в инверсной
форме – наборам, где эти переменные равны нулям.
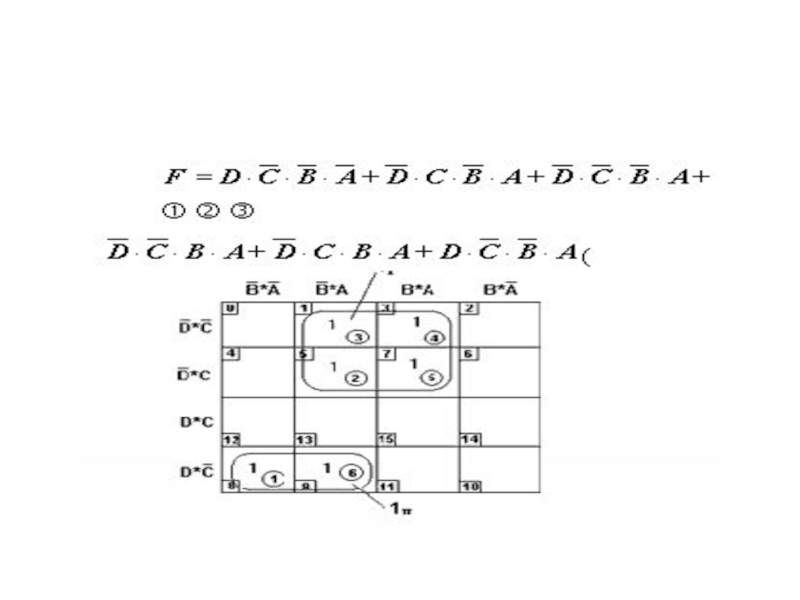
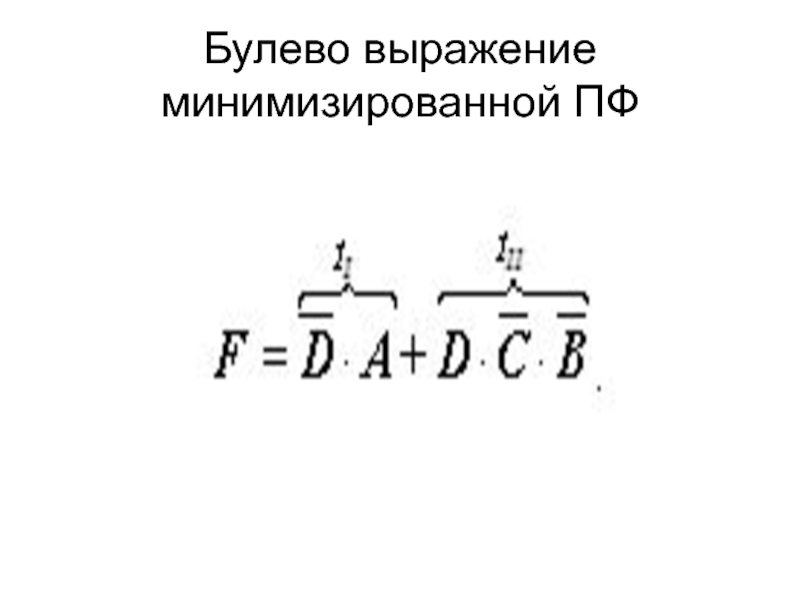
Слайд 37Булево выражение минимизированной ПФ
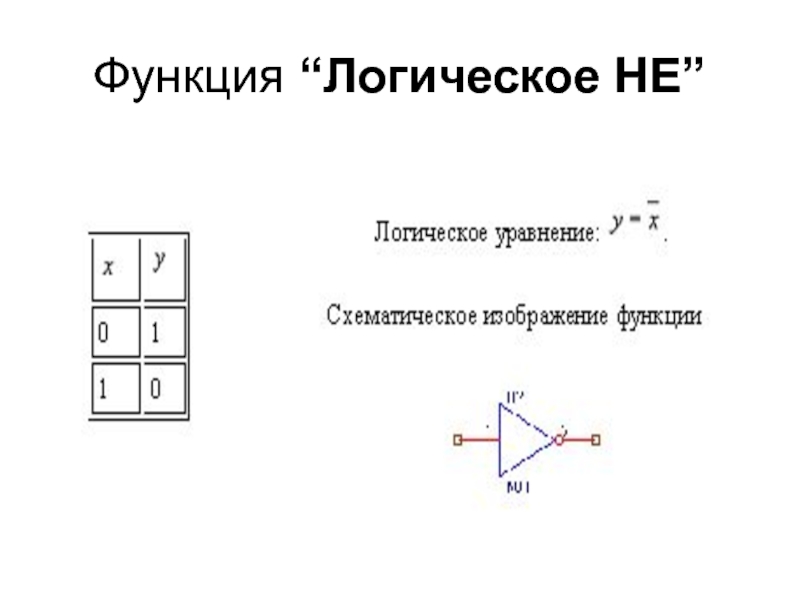
Слайд 391 Инвертор (логический элемент НЕ)
Слайд 402 Конъюнктор (логический элемент И)
Слайд 41Дизъюнктор (логический элемент ИЛИ
Слайд 43
Обычно при постановке задачи логическую функцию представляют в виде таблицы
истинности. Для получения уравнения логической функции и его минимизации используют
метод “карт Карно”.
Слайд 44
В соответствии с этим методом для получения уравнения логической функции
необходимо:
1. Составить таблицу истинности функции в которой должны быть представлены
все возможные сочетания входных сигналов и соответствующие им состояния выхода. В случае, когда состояние входа не оказывает влияния на выход, ставится X (любое значение).
2. Разбить все входные переменные на две группы произвольным образом.
3. Составить прямоугольную таблицу. Вдоль осей таблицы отложить последовательные состояния выделенных групп переменных в коде Грея.
4. Заполнить ячейки, расположенные на пересечении строк и столбцов таблицы значениями функции, соответствующими текущей комбинации состояний входных переменных.
5. Выделить в таблице все группы, содержащие 1 (либо 0).
6. Записать уравнение функции по выделенным группам