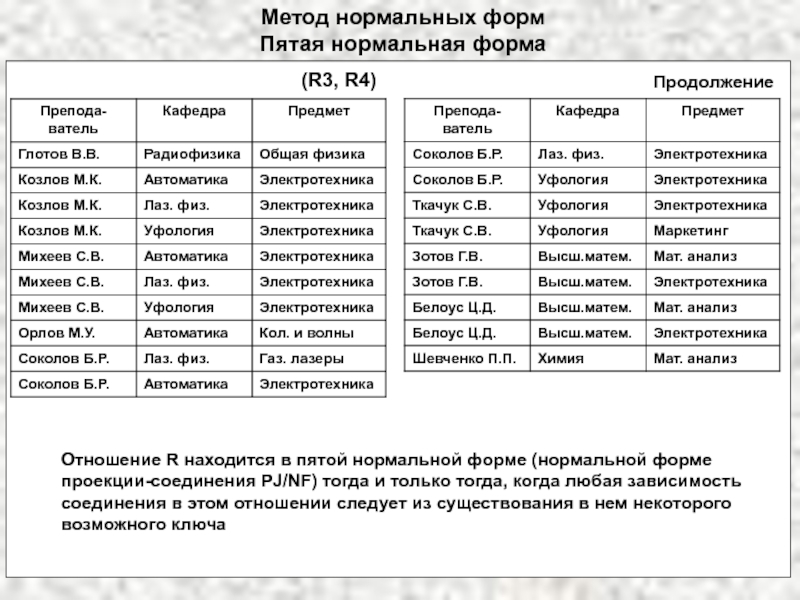
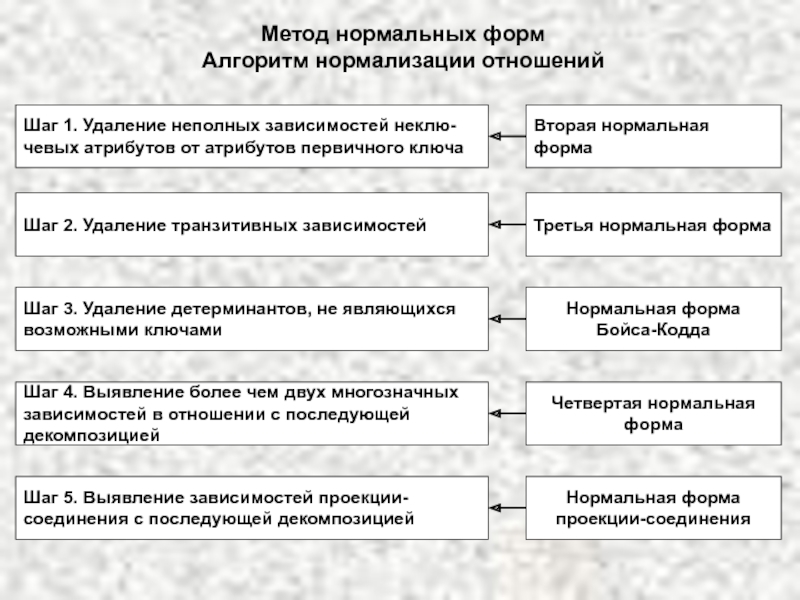
А соответствует единственное значение атрибута В
№_паспорта→ФИО; Кафедра→Факультет
Полная функциональная зависимость: атрибут
В зависит от атрибута А и не зависит от части (подмножества) атрибута АА={№_зач.книжки}; В={ФИО}: №_зач.книжки → ФИО – полная зависимость
А={№_паспорта, №_зач.книжки}; В={ФИО}:
№_паспорта, №_зач.книжки → ФИО – неполная зависимость
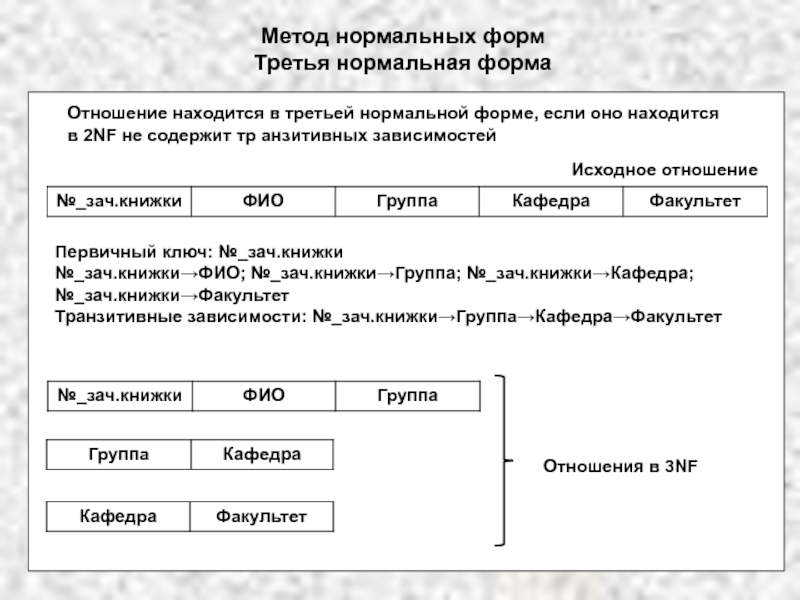
Транзитивная зависимость: атрибут С транзитивно зависит от А, если атрибут В зависит от А, атрибут С зависит от В, а обратные зависимости отсутствуют
Группа→Кафедра→Факультет; ФИО→Должность→Оклад
Многожначная зависимость А-»В: данному значению атрибута А соответствует множество значений атрибута В, не зависящих от других атрибутов
А) Один преподаватель ведет несколько предметов: ФИО-»Предмет (1:M)
Б) Несколько преподавателей ведут один предмет: ФИО«-Предмет (М:1)
В) Несколько преподавателей ведут несколько предметов: ФИО«-»Предмет (М:M)



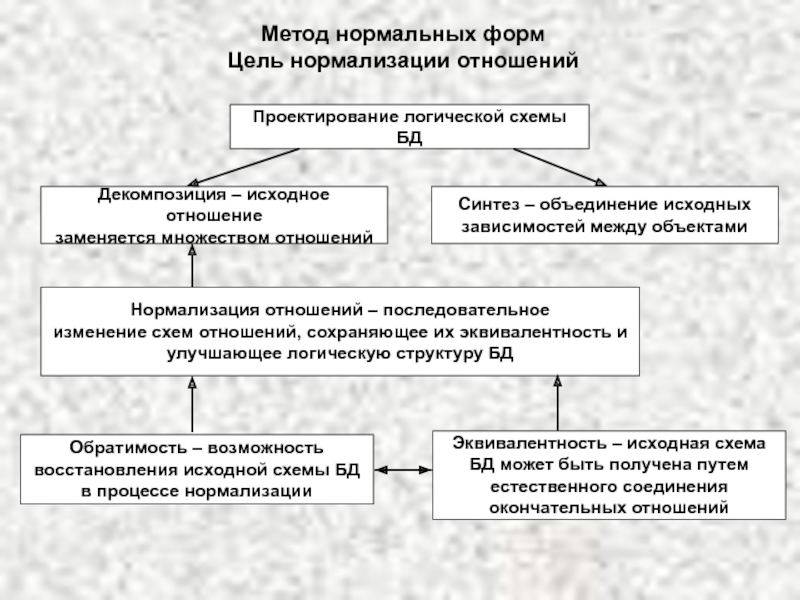

![L_4.ppt Метод нормальных формПример проецирования без потерьИсходное отношение RR1=R[A,B]R2=R[A,C]R=R1[R1.A=R2.A]R2 Метод нормальных формПример проецирования без потерьИсходное отношение RR1=R[A,B]R2=R[A,C]R=R1[R1.A=R2.A]R2](/img/thumbs/9b9f60cb527290f7f73327d73844859c-800x.jpg)