Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1_08.ppt
Содержание
- 1. 1_08.ppt
- 2. Модель сильной связиВолновая функция электрона в кристалле
- 3. Модель сильной связиОператоры рождения и уничтожения электрона:Гамильтониан
- 4. Гамильтонова матрица для модели сильной связиНужно сразу
- 5. Модель сильной связиСлагаемое, описывающее потенциальную энергию электронов,
- 6. Модель сильной связиСлагаемое, описывающее потенциальную энергию электронов,
- 7. Модель сильной связи без взаимодействияФурье-представление:Гамильтониан в этом
- 8. Модель сильной связи без взаимодействияОдномерный случай:Зона проводимости:
- 9. Пример. Одномерная цепочкаОдномерная периодическая цепочка из 6
- 10. Пример. Одномерная цепочка
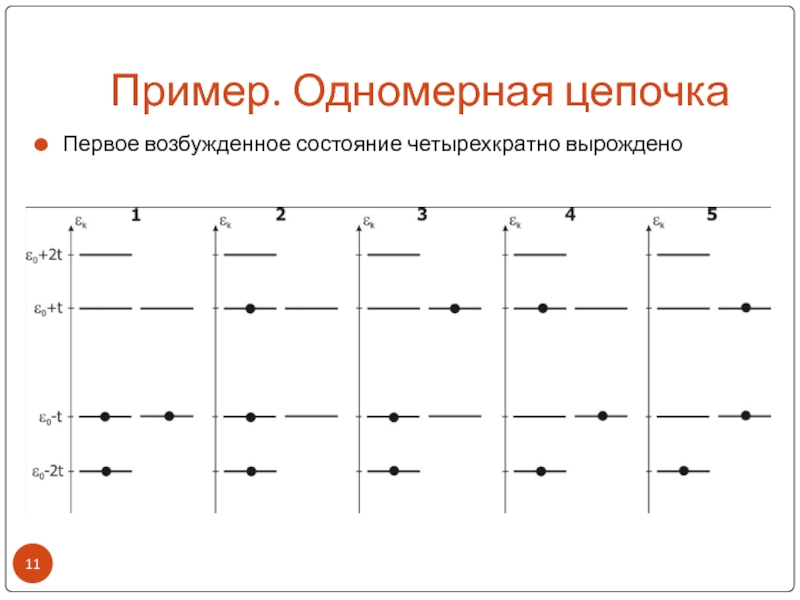
- 11. Пример. Одномерная цепочкаПервое возбужденное состояние четырехкратно вырождено
- 12. Скачать презентанцию
Модель сильной связиВолновая функция электрона в кристалле имеет максимумы вблизи ионного остова и близка к атомной волновой функции локализованного на соответствующей орбитали электрона. Вдали от иона волновая функция электрона асимптотически переходит
Слайды и текст этой презентации
Слайд 1Модель сильной связи.
Гамильтонова матрица.
Модель сильной связи без взаимодействия
1.8. Ферми-системы.
Модель сильной
связи
Слайд 2Модель сильной связи
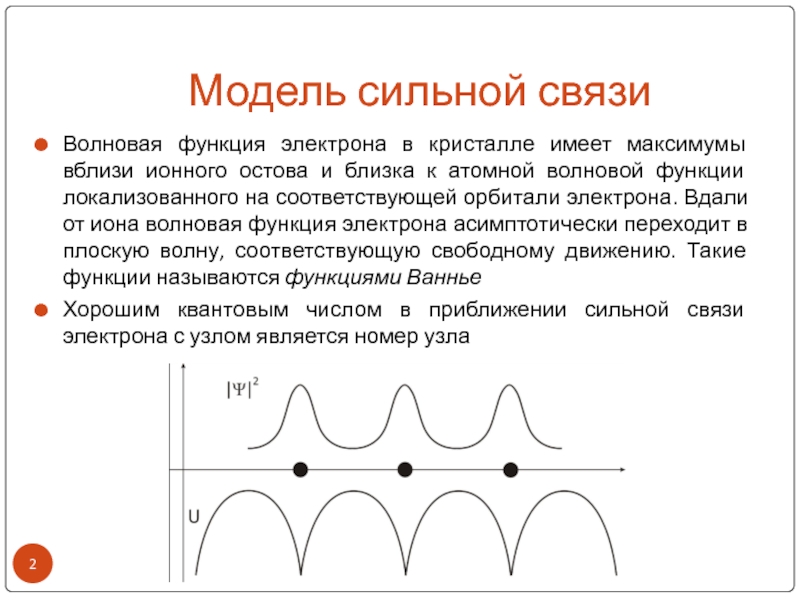
Волновая функция электрона в кристалле имеет максимумы вблизи
ионного остова и близка к атомной волновой функции локализованного на
соответствующей орбитали электрона. Вдали от иона волновая функция электрона асимптотически переходит в плоскую волну, соответствующую свободному движению. Такие функции называются функциями ВанньеХорошим квантовым числом в приближении сильной связи электрона с узлом является номер узла
Слайд 3Модель сильной связи
Операторы рождения и уничтожения электрона:
Гамильтониан системы, выраженный через
операторы рождения и уничтожения:
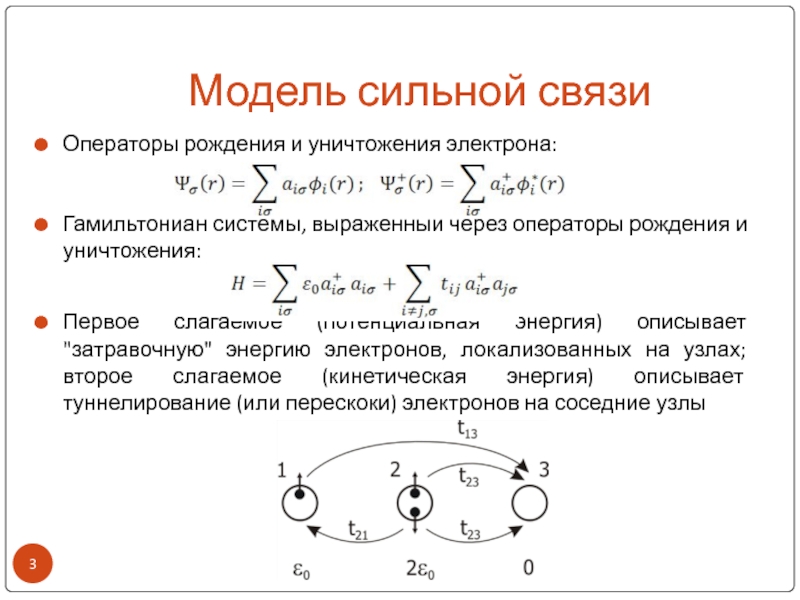
Первое слагаемое (потенциальная энергия) описывает "затравочную" энергию
электронов, локализованных на узлах; второе слагаемое (кинетическая энергия) описывает туннелирование (или перескоки) электронов на соседние узлы
Слайд 4Гамильтонова матрица
для модели сильной связи
Нужно сразу сформировать базис, упорядоченный по
числам заполнения, в котором можно организовать эффективную процедуру поиска нужного
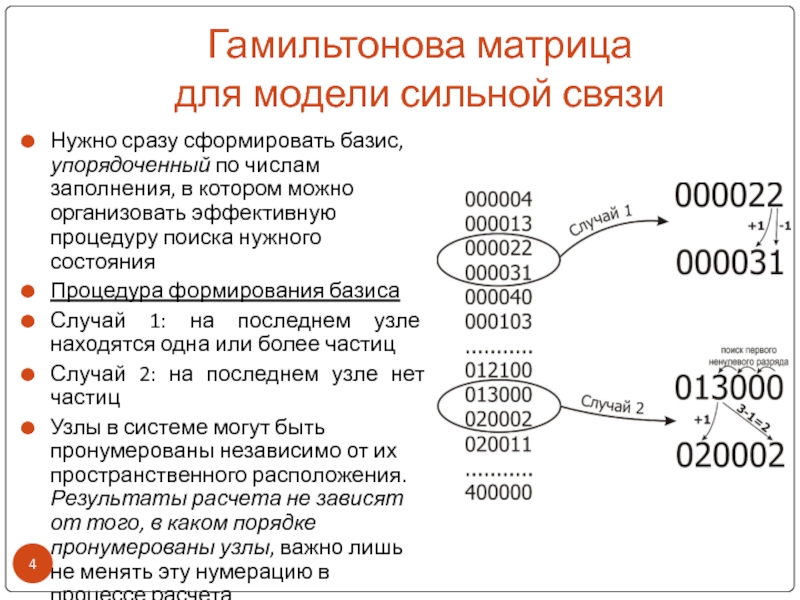
состоянияПроцедура формирования базиса
Случай 1: на последнем узле находятся одна или более частиц
Случай 2: на последнем узле нет частиц
Узлы в системе могут быть пронумерованы независимо от их пространственного расположения. Результаты расчета не зависят от того, в каком порядке пронумерованы узлы, важно лишь не менять эту нумерацию в процессе расчета
Слайд 5Модель сильной связи
Слагаемое, описывающее потенциальную энергию электронов, локализованных на узлах:
Действие
каждого из них не приводит к изменению волновой функции:
Кинетическое слагаемое
гамильтониана приводит к появлению в гамильтоновой матрице недиагональных слагаемых:Если в одномерной цепочке нечетное количество частиц, то знак матричного элемента перескока будет всегда одинаков, как если бы не было антисимметрии
Слайд 6Модель сильной связи
Слагаемое, описывающее потенциальную энергию электронов, локализованных на узлах:
Действие
каждого из них не приводит к изменению волновой функции:
Кинетическое слагаемое
гамильтониана приводит к появлению в гамильтоновой матрице недиагональных слагаемых:Если в одномерной цепочке нечетное количество частиц, то знак матричного элемента перескока будет всегда одинаков, как если бы не было антисимметрии
Слайд 7Модель сильной связи
без взаимодействия
Фурье-представление:
Гамильтониан в этом представлении диагонален – импульсное
представление является в данной задаче собственно энергетическим
Полная энергия системы:
Отрицательный знак
матричных элементов перескока выбран из удобства описания спектра системы в импульсном пространстве; такая возможность выбора знака обусловлена справедливостью следующего свойства модели сильной связи: спектр системы не меняется при изменении знака перед амплитудой перескока в случае приближения ближайших соседей
Слайд 8Модель сильной связи
без взаимодействия
Одномерный случай:
Зона проводимости: ширина зоны пропорциональна вероятности
перескока. При увеличении концентрации электронов зона будет последовательно заполняться в
соответствии с принципом Паули, так что заняты будут все состояния ниже некоторого максимального энергетического уровня, называемого уровнем ФермиПри учете взаимодейтсвия между частицами точного аналитического решения получить, как правило, не удается
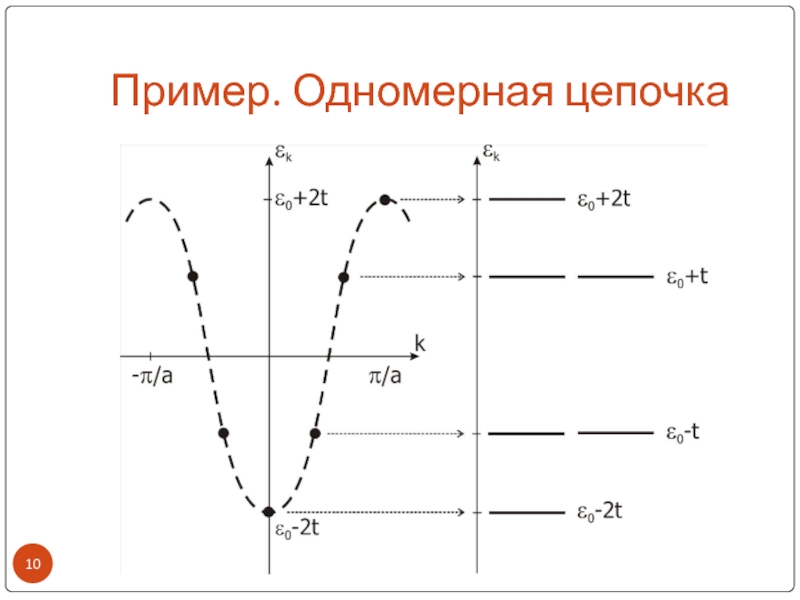
Слайд 9Пример. Одномерная цепочка
Одномерная периодическая цепочка из 6 узлов с 3
частицами
В системе 6 разрешенных одночастичных уровней энергии:
Энергия основного состояния:
Первое возбужденное
состояние:Первое возбужденное состояние
четырехкратно вырождено