2_06.ppt

Содержание

1. 2_06.ppt
2. Модель ИзингаМодель Изинга:На каждом узле есть только
3. Модель Изинга в приближении среднего поля (ферромагнетик)Самосогласованное
4. Модель Изинга в приближении среднего поля (ферромагнетик)Магнитная
5. Модель Изинга в приближении среднего поля (антиферромагнетик)Средний
6. Точное решение модели ИзингаМодель Изинга при Jij=J
7. Точное решение модели ИзингаВ температурной зависимости восприимчивости отсутствуют особенности как для ферромагнетика, так и для антиферромагнетика:
8. Точное решение модели ИзингаЗависимость теплоемкости от температуры
9. Метод Монте-Карло для модели ИзингаГамильтониан модели Изинга
10. Метод Монте-Карло для модели ИзингаЕсли учитывается только
11. Схема алгоритма Монте-Карло для модели Изинга
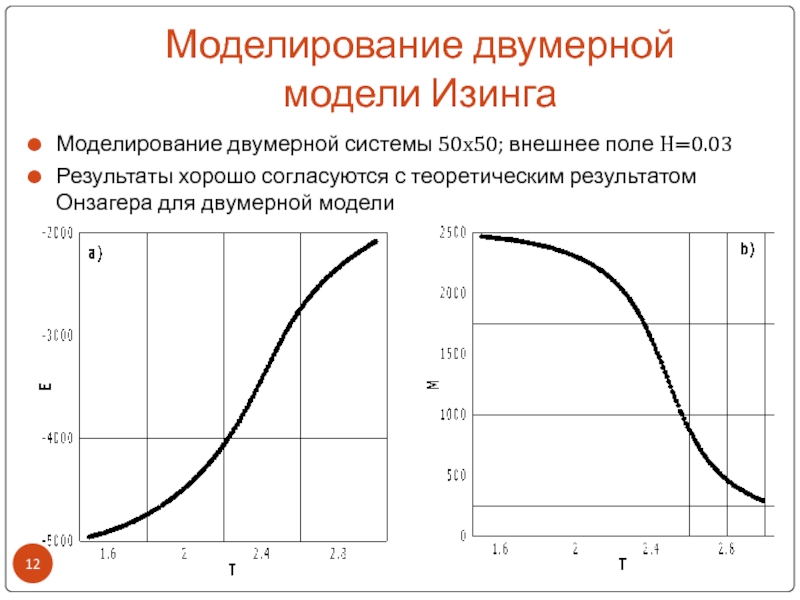
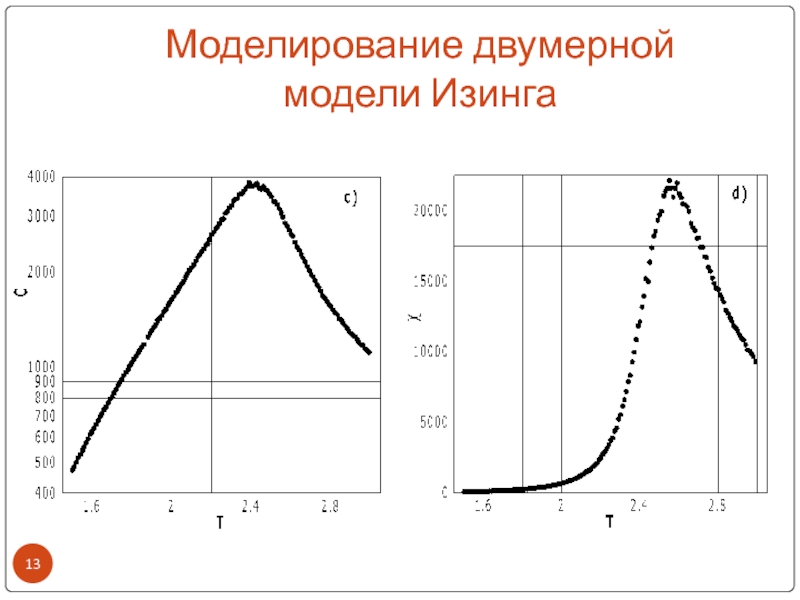
12. Моделирование двумерной модели ИзингаМоделирование двумерной системы 50х50;
13. Моделирование двумерной модели Изинга
14. Скачать презентанцию

Модель ИзингаМодель Изинга:На каждом узле есть только две степени свободыВ основном состоянии при нулевой температуре спины либо «заморожены» и ориентированы вдоль поля (ферромагнитное состояние), либо чередуются (антиферромагнитное состояние). В обоих случаях

Слайды и текст этой презентации

Слайд 1Модель Изинга в приближении среднего поля. Точное решение модели Изинга.

Метод Монте-Карло для модели Изинга
2.6. Метод Монте-Карло для модели Изинга

Модель Изинга в приближении среднего поля. Точное решение модели Изинга. Метод Монте-Карло для модели Изинга2.6. Метод Монте-Карло

Слайд 2Модель Изинга
Модель Изинга:

На каждом узле есть только две степени свободы
В

основном состоянии при нулевой температуре спины либо «заморожены» и ориентированы

вдоль поля (ферромагнитное состояние), либо чередуются (антиферромагнитное состояние). В обоих случаях основное состояние модели Изинга является упорядоченным состоянием со спонтанной намагниченностью
При достаточно большой температуре, называемой температурой Кюри для ферромагнетика и температурой Нееля для антиферромагнетика, происходит фазовый переход в неупорядоченное, парамагнитное состояние

Модель ИзингаМодель Изинга:На каждом узле есть только две степени свободыВ основном состоянии при нулевой температуре спины либо

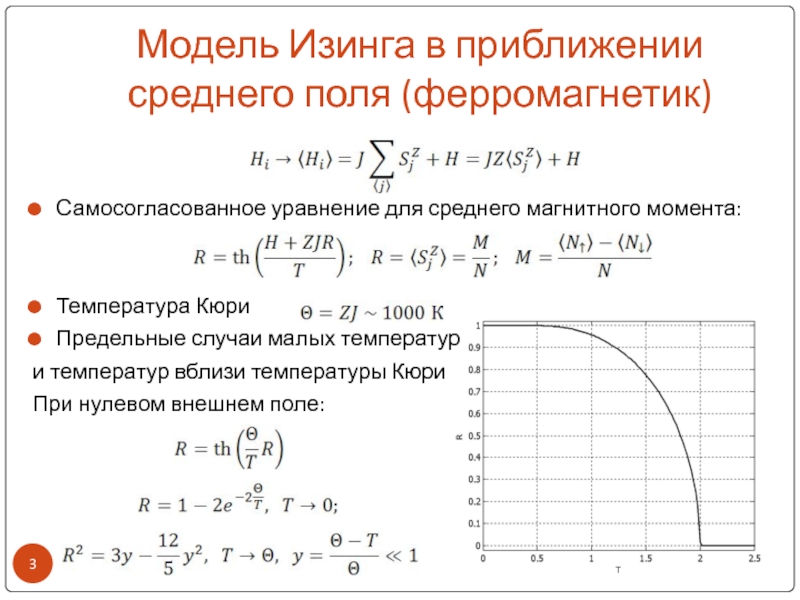
Слайд 3Модель Изинга в приближении среднего поля (ферромагнетик)

Самосогласованное уравнение для среднего

магнитного момента:

Температура Кюри
Предельные случаи малых температур
и температур вблизи температуры Кюри

При нулевом внешнем поле:

Модель Изинга в приближении среднего поля (ферромагнетик)Самосогласованное уравнение для среднего магнитного момента:Температура КюриПредельные случаи малых температури температур

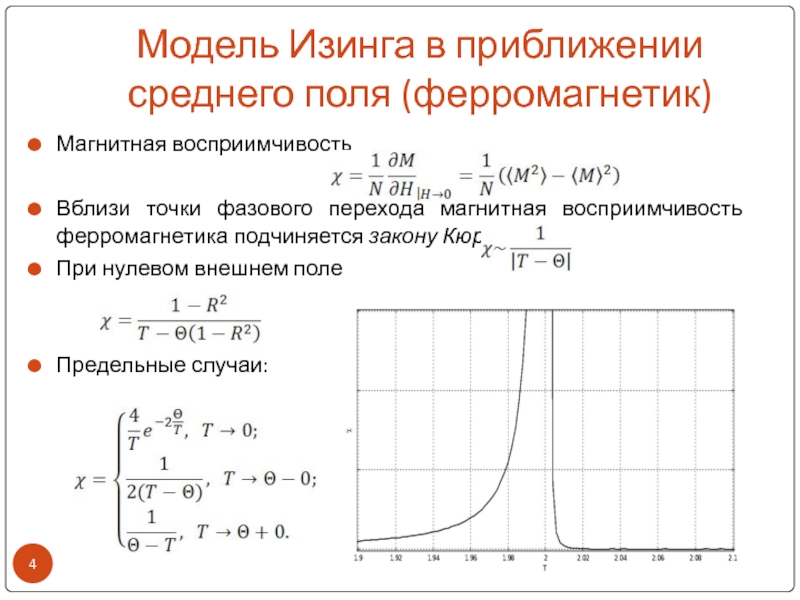
Слайд 4Модель Изинга в приближении среднего поля (ферромагнетик)
Магнитная восприимчивость

Вблизи точки фазового

перехода магнитная восприимчивость ферромагнетика подчиняется закону Кюри
При нулевом внешнем поле

Предельные

случаи:

Модель Изинга в приближении среднего поля (ферромагнетик)Магнитная восприимчивостьВблизи точки фазового перехода магнитная восприимчивость ферромагнетика подчиняется закону КюриПри

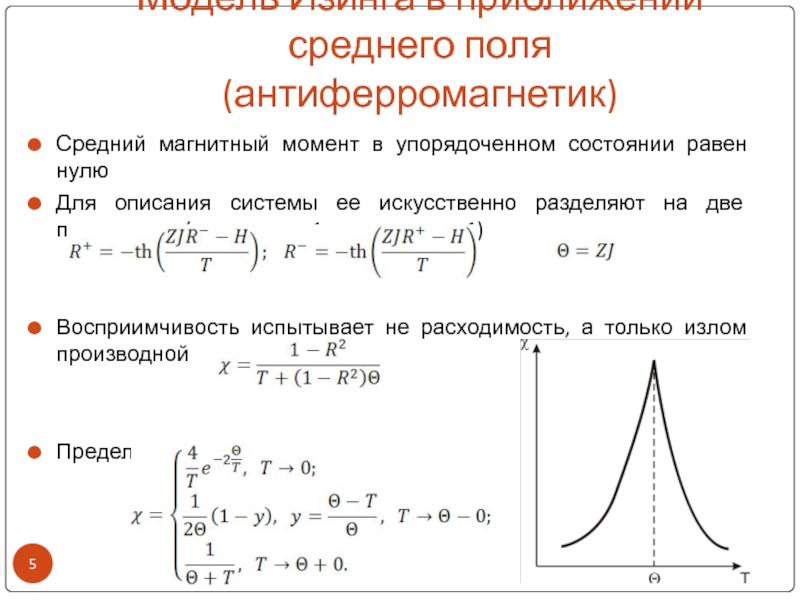
Слайд 5Модель Изинга в приближении среднего поля (антиферромагнетик)
Средний магнитный момент в

упорядоченном состоянии равен нулю
Для описания системы ее искусственно разделяют на

две подрешетки (со спином +1 и со спином –1)

Восприимчивость испытывает не расходимость, а только излом производной

Предельные случаи:

Модель Изинга в приближении среднего поля (антиферромагнетик)Средний магнитный момент в упорядоченном состоянии равен нулюДля описания системы ее

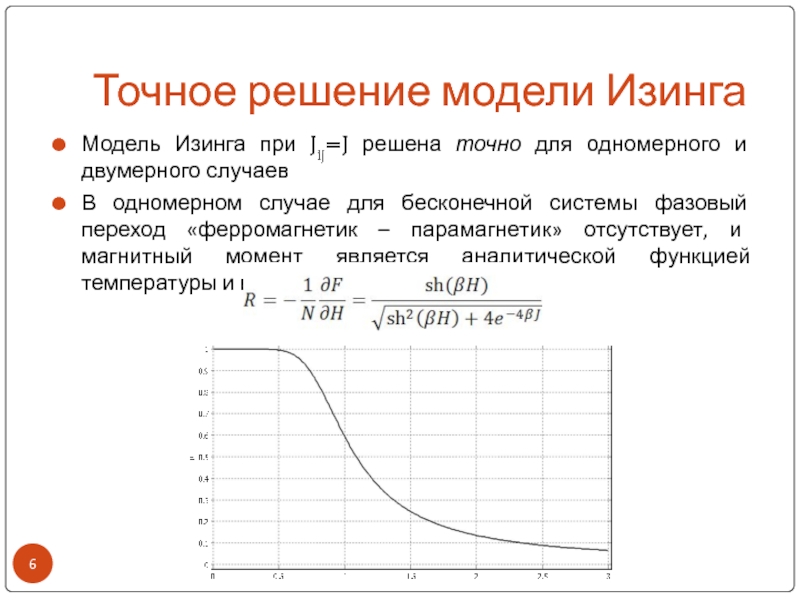
Слайд 6Точное решение модели Изинга
Модель Изинга при Jij=J решена точно для

одномерного и двумерного случаев
В одномерном случае для бесконечной системы фазовый

переход «ферромагнетик – парамагнетик» отсутствует, и магнитный момент является аналитической функцией температуры и внешнего поля

Точное решение модели ИзингаМодель Изинга при Jij=J решена точно для одномерного и двумерного случаевВ одномерном случае для

Слайд 7Точное решение модели Изинга
В температурной зависимости восприимчивости отсутствуют особенности как

для ферромагнетика, так и для антиферромагнетика:

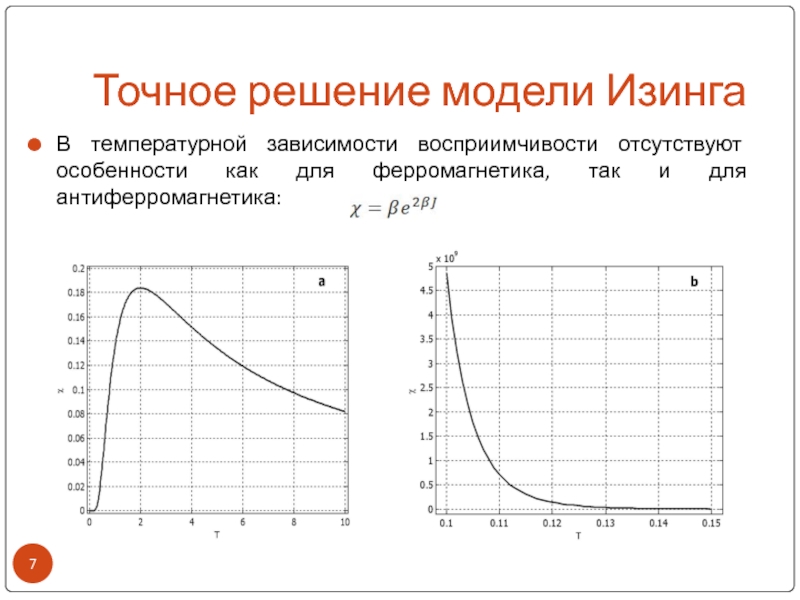
Точное решение модели ИзингаВ температурной зависимости восприимчивости отсутствуют особенности как для ферромагнетика, так и для антиферромагнетика:

Слайд 8Точное решение модели Изинга
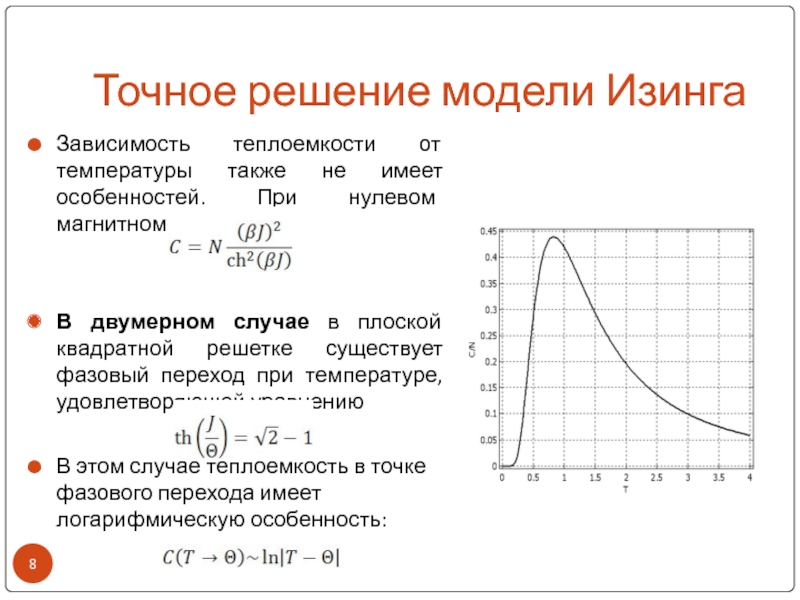
Зависимость теплоемкости от температуры также не имеет

особенностей. При нулевом магнитном поле

В двумерном случае в плоской

квадратной решетке существует фазовый переход при температуре, удовлетворяющей уравнению

В этом случае теплоемкость в точке фазового перехода имеет логарифмическую особенность:

Точное решение модели ИзингаЗависимость теплоемкости от температуры также не имеет особенностей. При нулевом магнитном поле В двумерном

Слайд 9Метод Монте-Карло для модели Изинга
Гамильтониан модели Изинга в узельном базисе диагонален:

Уравнение

детального баланса:

Интенсивность переходов
Алгоритм Метрополиса:

Алгоритм тепловой ванны:

Функция Глаубера:

Метод Монте-Карло для модели ИзингаГамильтониан модели Изинга в узельном базисе диагонален:Уравнение детального баланса:Интенсивность переходовАлгоритм Метрополиса:Алгоритм тепловой ванны:Функция

Слайд 10Метод Монте-Карло для модели Изинга
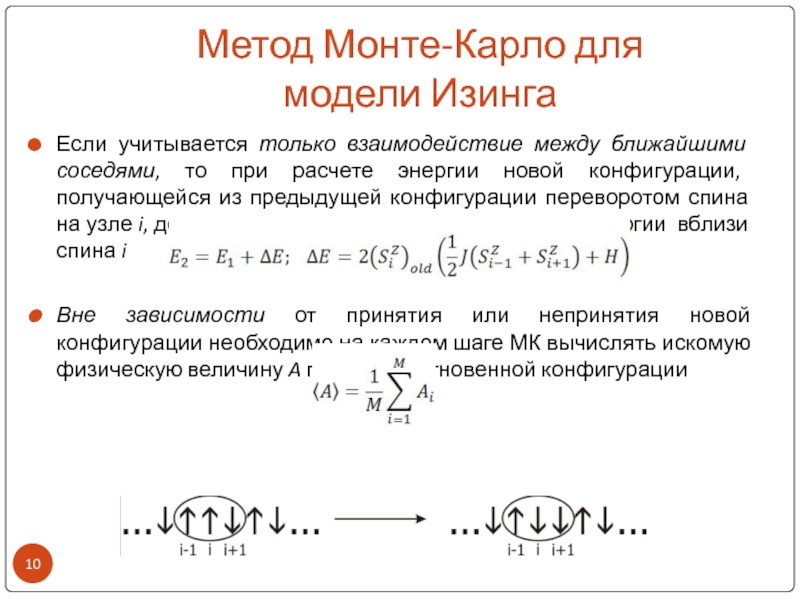
Если учитывается только взаимодействие между ближайшими соседями,

то при расчете энергии новой конфигурации, получающейся из предыдущей конфигурации

переворотом спина на узле i, достаточно лишь пересчитать изменение энергии вблизи спина i

Вне зависимости от принятия или непринятия новой конфигурации необходимо на каждом шаге МК вычислять искомую физическую величину A по данной мгновенной конфигурации

Метод Монте-Карло для модели ИзингаЕсли учитывается только взаимодействие между ближайшими соседями, то при расчете энергии новой конфигурации,

Слайд 11Схема алгоритма Монте-Карло для модели Изинга

Слайд 12Моделирование двумерной модели Изинга
Моделирование двумерной системы 50х50; внешнее поле H=0.03
Результаты хорошо

согласуются с теоретическим результатом Онзагера для двумерной модели

Моделирование двумерной модели ИзингаМоделирование двумерной системы 50х50; внешнее поле H=0.03Результаты хорошо согласуются с теоретическим результатом Онзагера для

Слайд 13Моделирование двумерной модели Изинга

Скачать презентацию

Разделы презентаций

2_06.ppt

Содержание

Слайды и текст этой презентации

Слайд 1Модель Изинга в приближении среднего поля. Точное решение модели Изинга.

Метод Монте-Карло для модели Изинга
2.6. Метод Монте-Карло для модели Изинга

Слайд 2Модель Изинга
Модель Изинга:

На каждом узле есть только две степени свободы
В

основном состоянии при нулевой температуре спины либо «заморожены» и ориентированы

Слайд 3Модель Изинга в приближении среднего поля (ферромагнетик)

Самосогласованное уравнение для среднего

магнитного момента:

Температура Кюри
Предельные случаи малых температур
и температур вблизи температуры Кюри

Слайд 4Модель Изинга в приближении среднего поля (ферромагнетик)
Магнитная восприимчивость

Вблизи точки фазового

перехода магнитная восприимчивость ферромагнетика подчиняется закону Кюри
При нулевом внешнем поле

Предельные

Слайд 5Модель Изинга в приближении среднего поля (антиферромагнетик)
Средний магнитный момент в

упорядоченном состоянии равен нулю
Для описания системы ее искусственно разделяют на

Слайд 6Точное решение модели Изинга
Модель Изинга при Jij=J решена точно для

одномерного и двумерного случаев
В одномерном случае для бесконечной системы фазовый

Слайд 7Точное решение модели Изинга
В температурной зависимости восприимчивости отсутствуют особенности как

для ферромагнетика, так и для антиферромагнетика:

Слайд 8Точное решение модели Изинга
Зависимость теплоемкости от температуры также не имеет

особенностей. При нулевом магнитном поле

В двумерном случае в плоской

Слайд 9Метод Монте-Карло для модели Изинга
Гамильтониан модели Изинга в узельном базисе диагонален:

Уравнение

детального баланса:

Интенсивность переходов
Алгоритм Метрополиса:

Алгоритм тепловой ванны:

Функция Глаубера:

Слайд 10Метод Монте-Карло для модели Изинга
Если учитывается только взаимодействие между ближайшими соседями,

то при расчете энергии новой конфигурации, получающейся из предыдущей конфигурации

Слайд 11Схема алгоритма Монте-Карло для модели Изинга

Слайд 12Моделирование двумерной модели Изинга
Моделирование двумерной системы 50х50; внешнее поле H=0.03
Результаты хорошо

согласуются с теоретическим результатом Онзагера для двумерной модели

Слайд 13Моделирование двумерной модели Изинга

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

2_06.ppt

Содержание

Слайды и текст этой презентации

Слайд 1Модель Изинга в приближении среднего поля. Точное решение модели Изинга.

Метод Монте-Карло для модели Изинга2.6. Метод Монте-Карло для модели Изинга

Слайд 2Модель ИзингаМодель Изинга:На каждом узле есть только две степени свободыВ

основном состоянии при нулевой температуре спины либо «заморожены» и ориентированы

Слайд 3Модель Изинга в приближении среднего поля (ферромагнетик)Самосогласованное уравнение для среднего

магнитного момента:Температура КюриПредельные случаи малых температури температур вблизи температуры Кюри

Слайд 4Модель Изинга в приближении среднего поля (ферромагнетик)Магнитная восприимчивостьВблизи точки фазового

перехода магнитная восприимчивость ферромагнетика подчиняется закону КюриПри нулевом внешнем полеПредельные

Слайд 5Модель Изинга в приближении среднего поля (антиферромагнетик)Средний магнитный момент в

упорядоченном состоянии равен нулюДля описания системы ее искусственно разделяют на

Слайд 6Точное решение модели ИзингаМодель Изинга при Jij=J решена точно для

одномерного и двумерного случаевВ одномерном случае для бесконечной системы фазовый

Слайд 7Точное решение модели ИзингаВ температурной зависимости восприимчивости отсутствуют особенности как

для ферромагнетика, так и для антиферромагнетика:

Слайд 8Точное решение модели ИзингаЗависимость теплоемкости от температуры также не имеет

особенностей. При нулевом магнитном поле В двумерном случае в плоской

Слайд 9Метод Монте-Карло для модели ИзингаГамильтониан модели Изинга в узельном базисе диагонален:Уравнение

детального баланса:Интенсивность переходовАлгоритм Метрополиса:Алгоритм тепловой ванны:Функция Глаубера:

Слайд 10Метод Монте-Карло для модели ИзингаЕсли учитывается только взаимодействие между ближайшими соседями,

то при расчете энергии новой конфигурации, получающейся из предыдущей конфигурации

Слайд 11Схема алгоритма Монте-Карло для модели Изинга

Слайд 12Моделирование двумерной модели ИзингаМоделирование двумерной системы 50х50; внешнее поле H=0.03Результаты хорошо

согласуются с теоретическим результатом Онзагера для двумерной модели

Слайд 13Моделирование двумерной модели Изинга

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Метод Монте-Карло для модели Изинга
2.6. Метод Монте-Карло для модели Изинга

Слайд 2Модель Изинга
Модель Изинга:

На каждом узле есть только две степени свободы
В

Слайд 3Модель Изинга в приближении среднего поля (ферромагнетик)

Самосогласованное уравнение для среднего

магнитного момента:

Температура Кюри
Предельные случаи малых температур
и температур вблизи температуры Кюри

Слайд 4Модель Изинга в приближении среднего поля (ферромагнетик)
Магнитная восприимчивость

Вблизи точки фазового

перехода магнитная восприимчивость ферромагнетика подчиняется закону Кюри
При нулевом внешнем поле

Предельные

Слайд 5Модель Изинга в приближении среднего поля (антиферромагнетик)
Средний магнитный момент в

упорядоченном состоянии равен нулю
Для описания системы ее искусственно разделяют на

Слайд 6Точное решение модели Изинга
Модель Изинга при Jij=J решена точно для

одномерного и двумерного случаев
В одномерном случае для бесконечной системы фазовый

Слайд 7Точное решение модели Изинга
В температурной зависимости восприимчивости отсутствуют особенности как

Слайд 8Точное решение модели Изинга
Зависимость теплоемкости от температуры также не имеет

особенностей. При нулевом магнитном поле

В двумерном случае в плоской

Слайд 9Метод Монте-Карло для модели Изинга
Гамильтониан модели Изинга в узельном базисе диагонален:

Уравнение

детального баланса:

Интенсивность переходов
Алгоритм Метрополиса:

Алгоритм тепловой ванны:

Функция Глаубера:

Слайд 10Метод Монте-Карло для модели Изинга
Если учитывается только взаимодействие между ближайшими соседями,

Слайд 12Моделирование двумерной модели Изинга
Моделирование двумерной системы 50х50; внешнее поле H=0.03
Результаты хорошо