Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ – 2017 по математике Базовый уровень Задание № 20 Задачи на логику и
Содержание
- 1. ЕГЭ – 2017 по математике Базовый уровень Задание № 20 Задачи на логику и
- 2. Кузнечик и координатная прямая Задача: Кузнечик прыгает
- 3. Доски и распилы Задача. На палке отмечены
- 4. Параллели и меридианы Задача: На глобусе фломастером
- 5. Зарплата за колодец Задача: Хозяин договорился с
- 6. Дом, подъезды, квартиры (1)Задача: Во всех подъездах
- 7. Дом, подъезды, квартиры (2)Задача: Саша пригласил Петю
- 8. Улитка ползёт по дереву (1)Задача: Улитка за
- 9. Улитка ползет по дереву (2)Задача: Нефтяная компания
- 10. Корзина с грибами Задача: В корзине лежит
- 11. Золотые и серебряные монеты Задача: В обменном
- 12. Прямоугольник разбит на четыре правильных многоугольника Задача:
- 13. Викторина - правильные и неправильные ответы Задача:
- 14. Получили систему из двух уравнений с тремя
- 15. Бактерии в стаканеЗадача: Каждую секунду бактерия делится
- 16. Бензоколонка на кольцевой дороге Задача: На кольцевой
- 17. Спасибо за внимание!
- 18. Скачать презентанцию
Кузнечик и координатная прямая Задача: Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Кузнечик начинает прыгать из начала координат. Сколько существует различных точек на координатной
Слайды и текст этой презентации
Слайд 2Кузнечик и координатная прямая
Задача: Кузнечик прыгает вдоль координатной прямой
в любом направлении на единичный отрезок за один прыжок. Кузнечик
начинает прыгать из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков?Пояснение.
Заметим, что кузнечик может оказаться только в точках с нечётными координатами, поскольку число прыжков, которое он делает, — нечётно. Максимально кузнечик может оказаться в точках, модуль которых не превышает одиннадцати. Таким образом, кузнечик может оказаться в точках: −11, −9, −7, −5, −3, −1, 1, 3, 5, 7, 9 и 11; всего 12 точек.
Ответ: 12.
Слайд 3Доски и распилы
Задача. На палке отмечены поперечные линии красного,
жёлтого и зелёного цвета. Если распилить палку по красным линиям,
получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?Пояснение.
Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14 + 4 + 6 = 24 линии, следовательно, кусков будет 25.
Ответ: 25.
Слайд 4Параллели и меридианы
Задача: На глобусе фломастером проведены 17 параллелей
(включая экватор) и 24 меридиана. На сколько частей проведённые линии
разделяют поверхность глобуса?Пояснение.
Представим, что на глобусе ещё не нарисованы параллели и меридианы. Заметим, что 24 меридиана разделят глобус на 24 части. Рассмотрим сектор, образованный двумя соседними меридианами. Проведение первой параллели разделит сектор на две части, проведение второй добавить ещё одну часть, и так далее, таким образом, 17 параллелей разделят сектор на 18 частей. Следовательно, весь глобус будет разбит на 24 · 18 = 432 части.
Ответ: 432.
Слайд 5Зарплата за колодец
Задача: Хозяин договорился с рабочими, что они
копают колодец на следующих условиях: за первый метр он заплатит
им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?Пояснение.
Последовательность цен за метр — арифметическая прогрессия с первым элементом и разностью
Сумма первых элементов арифметической прогрессии —
То есть, в нашем
Слайд 6Дом, подъезды, квартиры (1)
Задача: Во всех подъездах дома одинаковое число
этажей, а на каждом этаже одинаковое число квартир. При этом
число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 455 квартир?Пояснение.
Число квартир, этажей и подъездов может быть только целым числом. Заметим, что число 455 делится на 5, 7 и 13. Следовательно, в доме должно быть 5 подъезда, 7 квартир и 13 этажей.
Ответ: 13.
Слайд 7Дом, подъезды, квартиры (2)
Задача: Саша пригласил Петю в гости, сказав,
что живёт в седьмом подъезде в квартире № 462, а этаж
сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.)Пояснение.
Поскольку в первых 7 подъездах не меньше 462 квартир, в каждом подъезде не меньше 462 : 7 = 66 квартир. Следовательно, на каждом из 7 этажей не меньше 9 квартир.
Пусть на каждой лестничной площадке по 9 квартир. Тогда в первых семи подъездах всего 9 · 7 · 7 = 441 квартира, и квартира 462 окажется в восьмом подъезде, что противоречит условию.
Пусть на каждой площадке по 10 квартир. Тогда в первых семи подъездах 10 · 7 · 7 = 490 квартир, а в первых шести — 420. Следовательно, квартира 462 находится в седьмом подъезде. Она в нем 42ая по счету, поскольку на этаже по 10 квартир, она расположена на пятом этаже.
Если бы на каждой площадке было по 11 квартир, то в первых шести подъездах оказалось бы 11 · 7 · 6 = 462 квартиры, то есть 462 квартира в шестом подъезде, что противоречит условию.
Тем самым, Саша живёт на пятом этаже.
Ответ: 5.
Слайд 8Улитка ползёт по дереву (1)
Задача: Улитка за день заползает вверх
по дереву на 4 м, а за ночь сползает на
3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?Пояснение.
За день улитка заползёт на 4 метра, а за ночь — сползёт на 3 метра. Итого за сутки она заползёт на метр. За шестеро суток она поднимется на высоту шести метров. И днём следующего, седьмого, дня она окажется на вершине дерева.
Ответ: 7.
Слайд 9Улитка ползет по дереву (2)
Задача: Нефтяная компания бурит скважину для
добычи нефти, которая залегает, по данным геологоразведки, на глубине 3
км. В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?Пояснение.
За день скважина увеличивается на 300 − 30 = 270 м. К началу одиннадцатого рабочего дня нефтяники пробурят 2700 метров. За одиннадцатый рабочий день нефтяники пробурят ещё 300 метров, то есть дойдут до глубины 3 км.
Ответ: 11.
Слайд 10Корзина с грибами
Задача: В корзине лежит 50 грибов: рыжики
и грузди. Известно, что среди любых 28 грибов имеется хотя
бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине?Пояснение.
В корзине точно лежит 27 груздей и 23 рыжика, так как взять 28 груздей, как и 24 рыжика, не получится.
Ответ: 27
Слайд 11Золотые и серебряные монеты
Задача: В обменном пункте можно совершить
одну из двух операций:
1) за 4 золотых монеты получить 5
серебряных и одну медную;2) за 7 серебряных монет получить 5 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая?
Пояснение.
Последовательно получаем:
Если Николай за 1 серебряную получил 3 медных, а у него появилось 90 медных, то он истратил 30 серебряных (т. к. 90 : 3 = 30 серебряных).
Таким образом, у него количество монет уменьшилось на 30.
Ответ: 30
Слайд 12Прямоугольник разбит на четыре правильных многоугольника
Задача: Прямоугольник разбит на
четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них,
начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.Введём обозначения, как показано на рисунке. Периметр верхнего левого прямоугольника равна 24, поэтому
аналогично,
При помощи полученной системы уравнений выразим значение
Из третьего уравнения получаем:
Следовательно, искомый периметр равен 12.
Слайд 13Викторина - правильные и неправильные ответы
Задача: Список заданий викторины
состоял из 25 вопросов. За каждый правильный ответ ученик получал
7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?Пояснение.
Он дал x правильных ответов, y (y≥1) неправильных и на z вопросов не ответил совсем. x+y+z=25
За каждый правильный ответ он получал 7, за неправильный (−10), за неосвещенный вопрос — 0.
7x-10y+0z=42
Слайд 14 Получили систему из двух уравнений с тремя неизвестными. Подберем решения
этой системы уравнений.
x+y+z=25
7x-10y=42=7*6
Из второго уравнения: 7x-7*6=7(x-6)=10y.
Так как число 7(x-6) делится
на 7, то и 10у делится на 7. Рассмотрим два случая:Если у=7, то х-6=10, значит, х=16, тогда
z=25-х-у=25-16-7=2
2) Если у=14, то 7(х-6)=140, отсюда, х-6=20, значит, х=26>25, что противоречит условию.
Таким образом, ученик правильно ответил на 16 вопросов.
Ответ: 16
Слайд 15Бактерии в стакане
Задача: Каждую секунду бактерия делится на две новые
бактерии. Известно, что весь объём одного стакана бактерии заполняют за
1 час. За сколько секунд стакан будет заполнен бактериями наполовину?Пояснение.
Заметим, что каждую секунду в стакане становится в два раза больше бактерий. То есть если в какой-то момент бактериями заполнена половина стакана, то через секунду будет заполнен весь стакан. Таким образом, полстакана будет заполнено через 59 минут и 59 секунд то есть через 3599 секунд.
Ответ: 3599
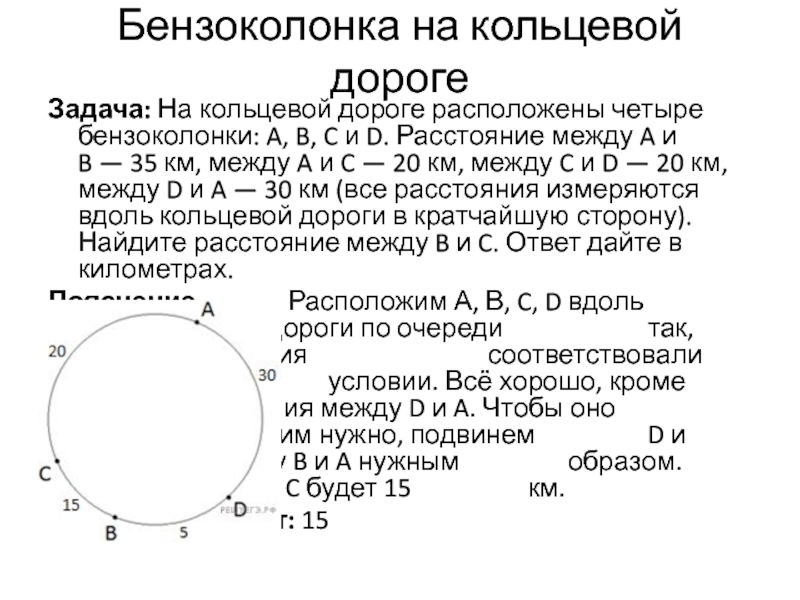
Слайд 16Бензоколонка на кольцевой дороге
Задача: На кольцевой дороге расположены четыре
бензоколонки: A, B, C и D. Расстояние между A и
B — 35 км, между A и C — 20 км, между C и D — 20 км, между D и A — 30 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в километрах.Пояснение. Расположим А, В, C, D вдоль кольцевой дороги по очереди так, чтобы расстояния соответствовали данным в условии. Всё хорошо, кроме расстояния между D и A. Чтобы оно было таким, каким нужно, подвинем D и поставим между B и A нужным образом. Тогда между B и C будет 15 км.
Ответ: 15