где f(x) некоторая функция переменной x. Число x* называется корнем
или решением данного уравнения, если при подстановке x= x* в уравнение последнее обращается в тождество f(x*)=0. Число x* называют также нулем функции y=f(x).В общем случае уравнение может иметь одно или несколько корней, как действительных, так и комплексных. Нахождение действительных корней с заданной точностью можно разбить на два этапа. Сначала корни отделяются, т.е. определяются отрезки, которые содержат по оному корню уравнения; а затем уточняются, т.е. вычисляются с требуемой точностью ε. Отделение корней уравнения f(x)=0, в области определения, непрерывной функции f(x), можно осуществлять несколькими способами:
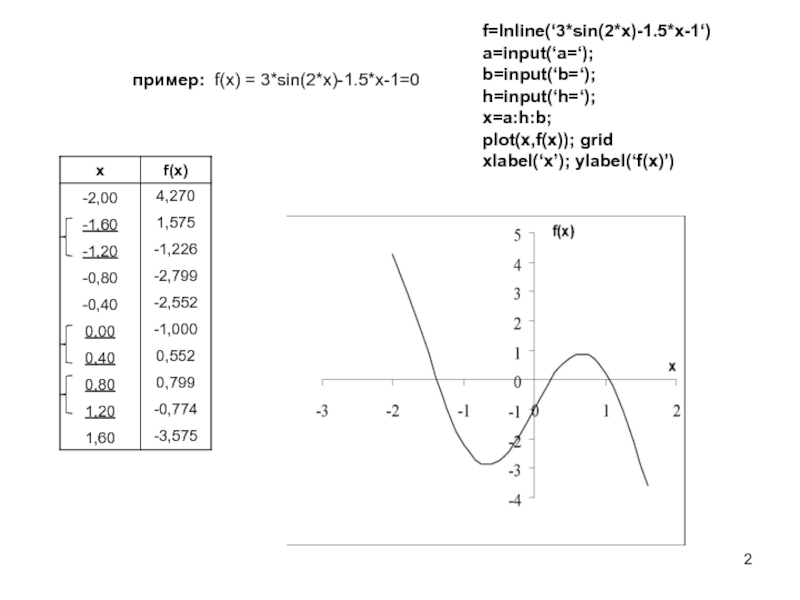
Табулирование – составление таблицы из равноотстоящих значений независимой переменной x и соответствующих значений функции и определение отрезков в которых смежные значения функции имеют различные знаки и следовательно содержат нулевые значения функции.
Графический - строим график функции f(x) и определяем минимальные отрезки, включающие точки пересечения графика функции с осью x.

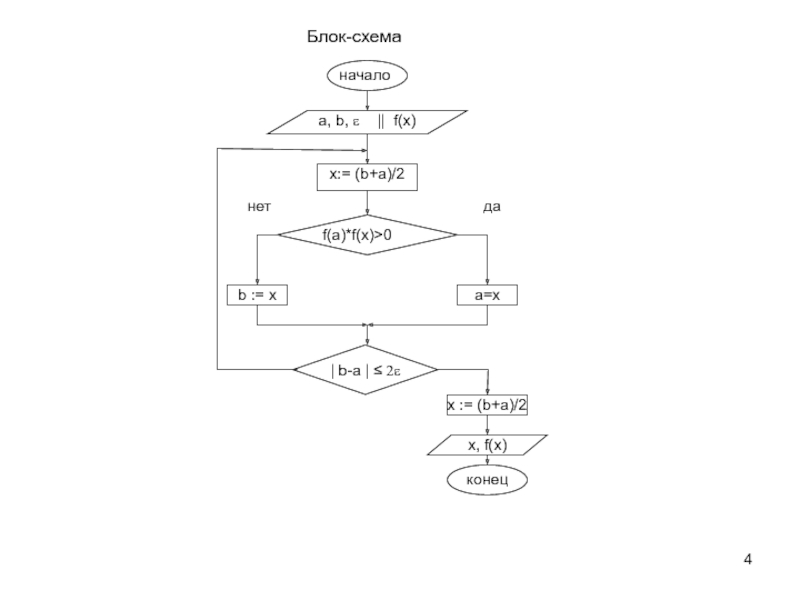
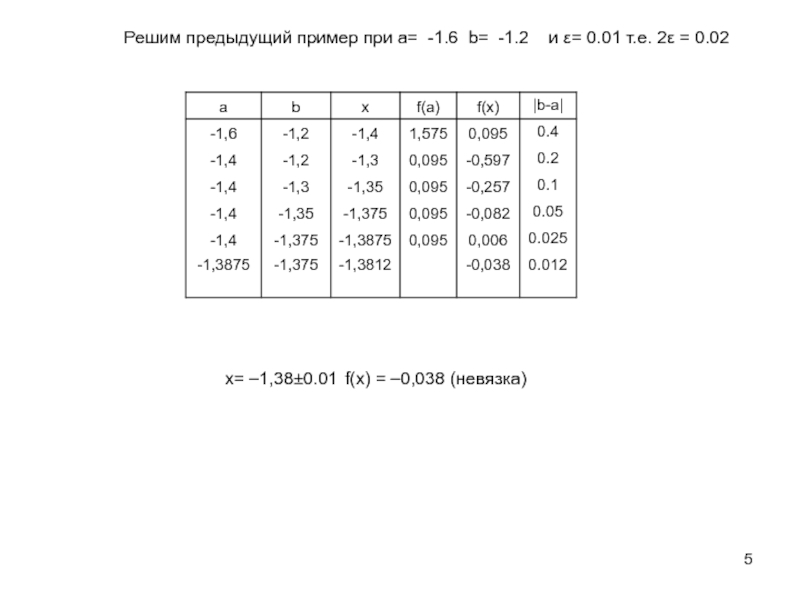
![VM-8-m-Уравнение.ppt Уточнение корня на отрезке [a,b], в котором локализован только один корень, Уточнение корня на отрезке [a,b], в котором локализован только один корень, осуществляется итерационными методами, в которых последовательно,](/img/thumbs/96bced9aa3c2093f69d7d168a2d47e97-800x.jpg)

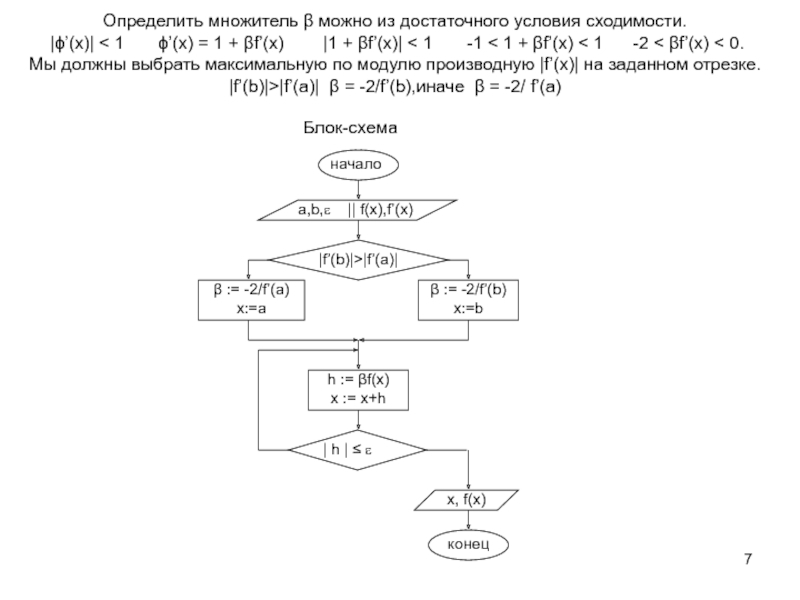
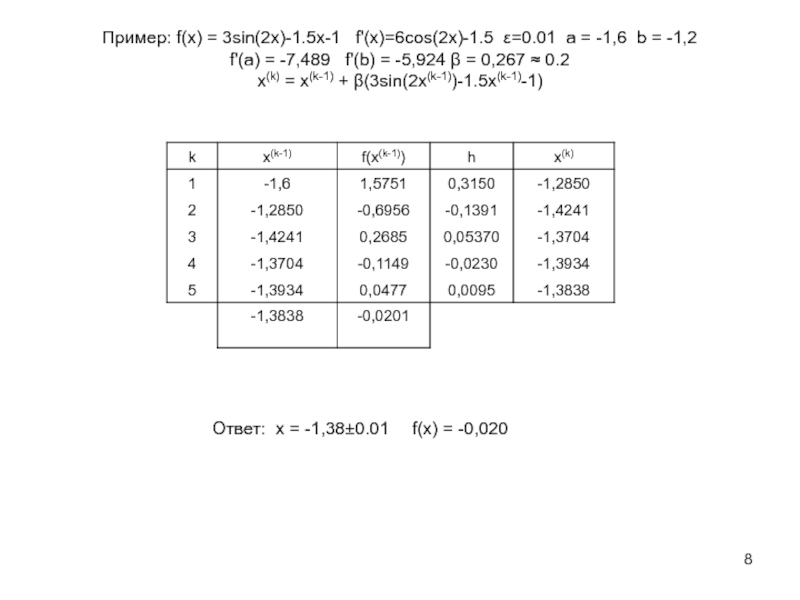

![VM-8-m-Уравнение.ppt Графическая иллюстрация. За начальное приближение к корню x(0) принимаем одну из Графическая иллюстрация. За начальное приближение к корню x(0) принимаем одну из границ отрезка [a; b], содержащего один](/img/thumbs/2a9825381a28a9b2a986addd8391a136-800x.jpg)
![VM-8-m-Уравнение.ppt алгоритмЗадаем функцию f(x) отрезок [a;b] и точность ε. За начальное приближение алгоритмЗадаем функцию f(x) отрезок [a;b] и точность ε. За начальное приближение x принимаем одну из границ заданного](/img/tmb/2/147235/191b219eecdabfd5419bf266c69ba396-800x.jpg)




















