5. В.В.Фролов 6. Н.В.Коровин
Часть 1 Строение
вещества 2002 г.(552)Часть 2 Термодин.и кинетика химического процесса 2003 г.(599)
- теоретические основы
Часть 3 Электрохим. и коррозионные процессы 2007(837)








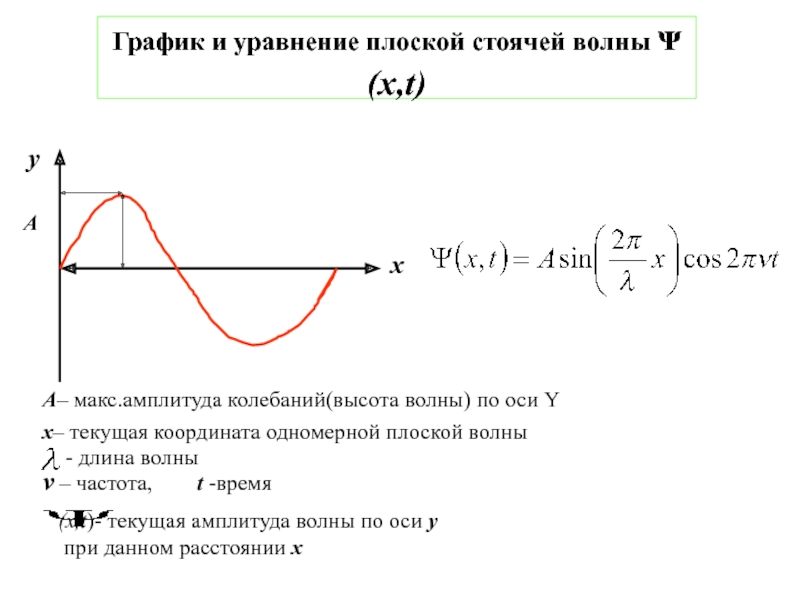













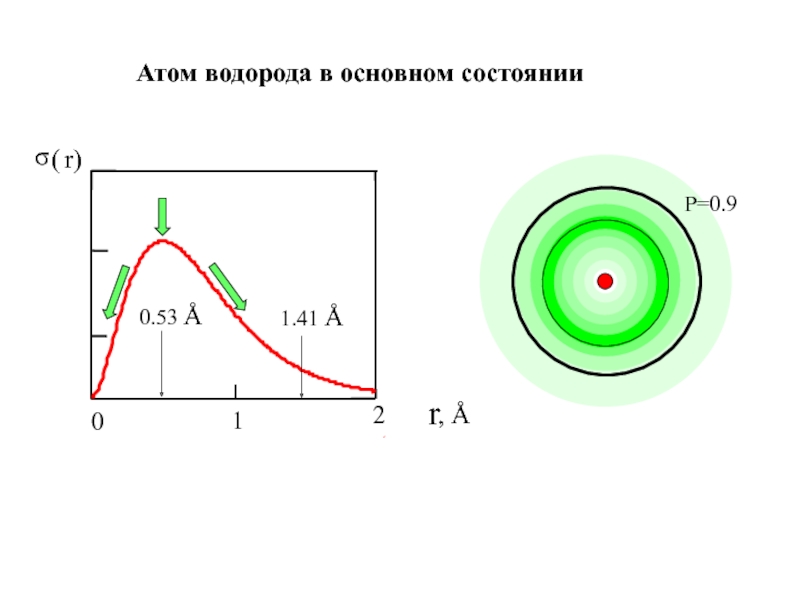
![1-АТОМ.ppt 1.6 Возбужденные состояния атома водорода Общий вид волновой функции-Ψ(r,ϑ,ϕ) = R(r)⋅Y(θ,ϕ)-[метод 1.6 Возбужденные состояния атома водорода Общий вид волновой функции-Ψ(r,ϑ,ϕ) = R(r)⋅Y(θ,ϕ)-[метод разделения переменных]R(r)n, l -](/img/thumbs/bf4c6ae606ebbac7df14594c87d8dc9c-800x.jpg)




















![Постановка звуков [ ф ] [ ф `]
Буква Ф
ЗАНЯТИЕ №3](/img/tmb/7/642013/84fdced61366e950859a20a66f9d6dc7-800x.jpg)









