Слайд 1ДИСКРЕТИЗАЦИЯ
и
КВАНТОВАНИЕ
АНАЛОГОВЫХ СИГНАЛОВ
Слайд 2ОСНОВНЫЕ ТЕМЫ ЛЕКЦИИ
ПОСТАНОВКА ЗАДАЧИ ДИСКРЕТИЗАЦИИ
ТЕОРЕМА КОТЕЛЬНИКОВА-НАЙКВИСТА
КВАНТОВАНИЕ НЕПРЕРЫВНОГО СИГНАЛА
ВЫБОР ВЕЛИЧИНЫ ШАГА
КВАНТОВАНИЯ
ЦИФРО-АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ (ЦАП)
ПАРАМЕТРЫ Ц А П
АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ (АЦП)
ПРЕОБРАЗОВАНИЕ АНАЛОГОВОГО
СИГНАЛА ВО ВРЕМЕННОЙ ИНТЕРВАЛ
ПАРАМЕТРЫ АЦП
Слайд 3Непрерывный сигнал
.
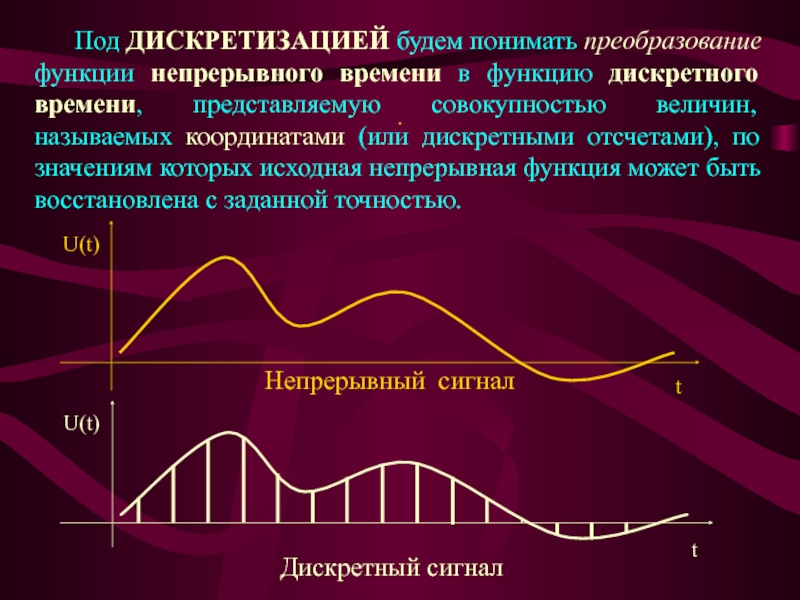
Под ДИСКРЕТИЗАЦИЕЙ будем понимать преобразование функции непрерывного времени
в функцию дискретного времени, представляемую совокупностью величин, называемых координатами (или
дискретными отсчетами), по значениям которых исходная непрерывная функция может быть восстановлена с заданной точностью.
U(t)
t
U(t)
t
Дискретный сигнал
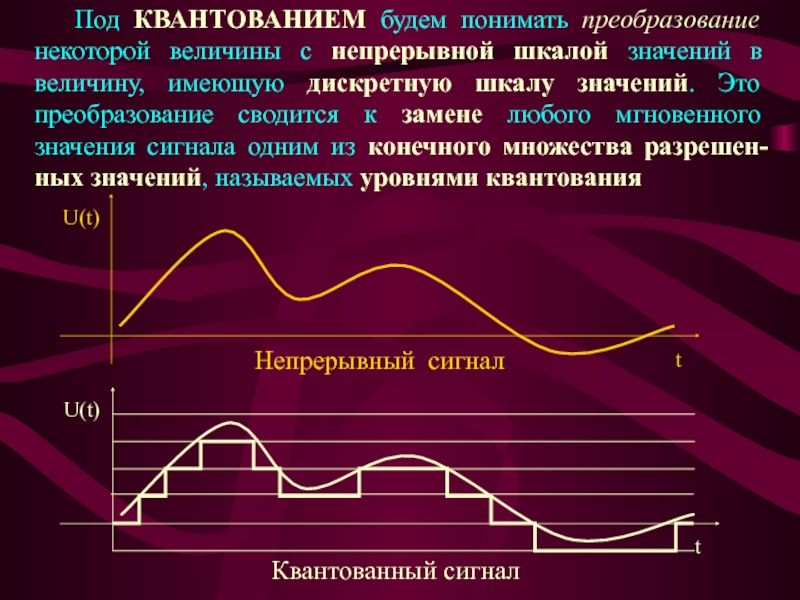
Слайд 4 Под КВАНТОВАНИЕМ будем понимать преобразование некоторой величины с непрерывной шкалой
значений в величину, имеющую дискретную шкалу значений. Это преобразование сводится
к замене любого мгновенного значения сигнала одним из конечного множества разрешен-ных значений, называемых уровнями квантования
U(t)
t
Непрерывный сигнал
Квантованный сигнал
U(t)
t
Слайд 5ПОСТАНОВКА ЗАДАЧИ ДИСКРЕТИЗАЦИИ
Спектральная плотность непрерывного сигнала
Учитывая полную симметрич-ность прямого
и обратного преобразо-вания Фурье, можно утверждать, что дискретизация сигнала по
времени приведет к образованию периодической функции спектральной плотности. (Аналогично: периодический по времени сигнал имеет дискретный спектр).
Дискретный сигнал
U(t)
t
U(kTd)
Td
Fd = 1/Td ; ωd = 2πFd = 2π/Td
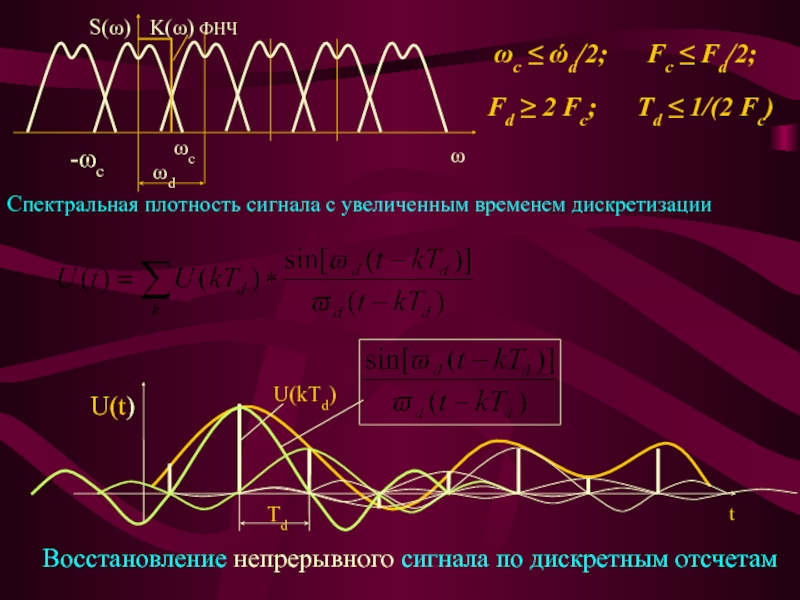
Слайд 6Спектральная плотность сигнала с увеличенным временем дискретизации
ωc ≤ ώd/2;
Fc ≤ Fd/2;
Fd ≥ 2 Fc; Td
≤ 1/(2 Fc)
Восстановление непрерывного сигнала по дискретным отсчетам
Слайд 7
U(t)
t
U(kTd)
Td
Аппроксимация полиномом нулевого порядка
Td
U(t)
t
U(kTd)
Кусочно-линейная аппроксимация полиномом первой степени
t
⮚ Более высокую
точность обеспечивает аппроксимация полиномом, имеющим порядок выше первого. Кривая такой
аппроксимирующей функции может состоять из отрезков дуг окружностей, отрезков парабол и т.п.
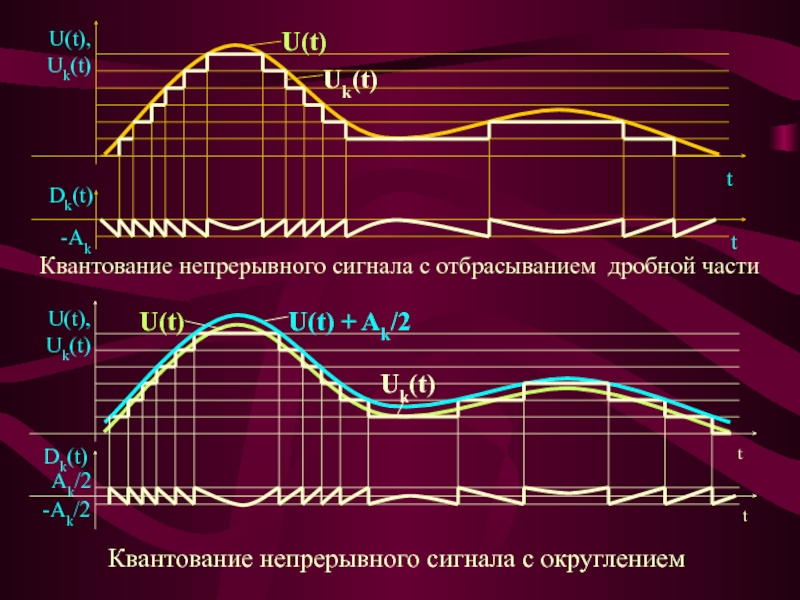
Слайд 8Квантование непрерывного сигнала с отбрасыванием дробной части
Квантование непрерывного сигнала с
округлением
Слайд 9ВЫБОР ВЕЛИЧИНЫ ШАГА КВАНТОВАНИЯ
Относительная погрешность квантования
Относительные величины
принято выражать в дециБелах или Неперах:
Величина, обратная относительной погрешности,
называется динамическим диапазоном передаваемых сообщений
Динамический диапазон непрерывных сообщений (сигналов) определяется отношением максимального сигнала к уровню шумов в непрерывном сигнале.
Слайд 10 Динамический диапазон непрерывных сообщений (сигналов) определяется отношением максималь-ного
сигнала к уровню шумов в непрерывном сигнале.
Например,
когда мы говорим о динамическом диапазоне акустических сигналов, за уровень шума (или минимального акустического сигнала) принимается уровень шума в лесу в безветренную погоду.
При этом мощность акустического сигнала при спокойном разговоре нескольких человек в 1000 раз больше или составляет 30дБ.
Уровень шума на проезжей части улицы в час пик оценивается в 1000000 раз больше мощности шума в безветренном лесу или 60дБ.
Слайд 11 Шум моторов реактивного самолета по мощности в 1012
раз больше минимального шума леса или 120дБ. Обычно этот уровень
называют порогом болевых ощущений для акустического аппарата человека (уха).
Таким образом, говоря об уровне акустического сигнала в дБ, мы сравниваем этот сигнал с минимальным шумом.
Максимальный динамический диапазон акустичес-ких сигналов, воспринимаемых человеческим ухом – 120дБ.
Акустический сигнал с таким диапазоном можно преобразовать в аналоговый электрический сигнал (например, в напряжение) с помощью микрофона.
Слайд 12 Однако, передача такого сигнала через реальные каналы связи:
проводной (телефонный), радио-канал, запись и воспроизведение на магнитофон или другие
носители информации – происходит с потерей динамического диапазона.
Динамический диапазон аналоговых каналов связи составляет от 20дБ до 60дБ. Это объясняется наличием шумов в каналах связи.
Квантование аналоговых сигналов на передаю-щем конце и передача цифровых сигналов по каналам связи позволяют передавать сигналы с динамическим диапазоном 90дБ и более. Напри-мер, запись музыкальных программ на лазерные компакт-диски (CD).
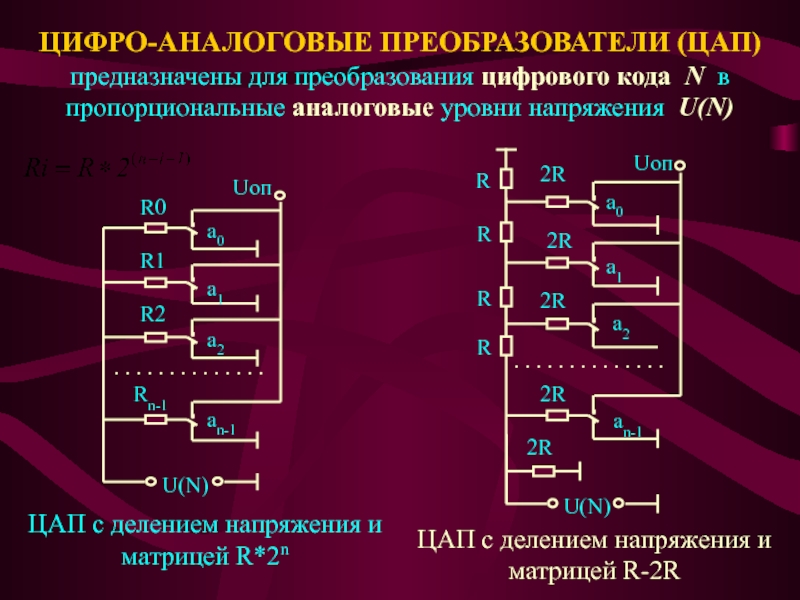
Слайд 13ЦИФРО-АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ (ЦАП) предназначены для преобразования цифрового кода N в
пропорциональные аналоговые уровни напряжения U(N)
Uоп
R0
R1
R2
Rn-1
. . . . .
. . . . . . . . .
a0
a1
a2
an-1
U(N)
ЦАП с делением напряжения и матрицей R*2n
ЦАП с делением напряжения и матрицей R-2R
Uоп
2R
2R
2R
2R
. . . . . . . . . . . . . .
a0
a1
a2
an-1
U(N)
2R
R
R
R
R
Слайд 14ЦАП с суммированием токов и резисторами R-2R
ЦАП с суммированием токов
и весовыми резисторами
Коммутация весовых резисторов осуществляется аналоговыми ключами на
МОП структурах
Изменяя номинал резистора Rос, можно менять коэффициент преобразования.
Если вместо опорного напряжения (Uоп) подать аналоговый сигнал, можно цифровым кодом регулировать коэффициент передачи, а следовательно, и уровень аналогового сигнала на выходе схемы.
Слайд 15Максимальным быстродействием обладает
Ц А П НА ПЕРЕКЛЮЧАТЕЛЯХ
ТОКОВ
и суммированием весовых токов на выходных резисторах
Весовые токи задаются резисторами R0..Rn-1 в цепях эмиттеров переключателей токов.
Выходные токи суммируются в цепях объединенных коллекторов и выделяются в виде выходного напряжения на внешних резисторах Rн1 или Rн2 номиналом 50...75 Ом.
ЦАП на переключателях токов позволяет получить на выходе два аналоговых сигнала: прямой сигнал и его инверсию
Слайд 16ПАРАМЕТРЫ Ц А П
Точность преобразования ЦАП зависит от:
⮚ степени температурного согласования сопротивлений матриц;
⮚ стабильности опорного
напряжения;
⮚ характеристик ОУ и
⮚ внутреннего сопротивления МОП коммутаторов.
Погрешность переходного процесса, т.е. выбросы на фоне выходного сигнала обусловлены эффектами гонок в логических цепях, а также разными временами включения и выключения коммутаторов ЦАП.
Для устранения выбросов переходных процессов на выходе ЦАП обязательно устанавливается Фильтр Низких Частот (ФНЧ) с граничной частотой вдвое меньшей частоты дискретизации сигнала (с учетом соотношения Котельникова).
Основной характеристикой ЦАП является передаточная харак-теристика: U=f(N), которая представляет собой ступенчатую линию. При этом реальная характеристика отличается от идеальной. Для оценки этих различий вводят статические и динамические параметры ЦАП.
Слайд 17СТАТИЧЕСКИЕ ПАРАМЕТРЫ Ц А П
⮚ ⮚ РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ или
ШАГ КВАНТОВАНИЯ (∆Uр.с) минимальное приращение выходного напряжения при преобразовании соседних
кодов (эта величина равна е.м.р.).
∆ Uр.с = Uмакс(N) / (2n),
где: n - количество двоичных разрядов ЦАП.
⮚ ПОГРЕШНОСТЬ СМЕЩЕНИЯ НУЛЯ - Uсм(0) - выходное напряжение при нулевом входном коде (N=0). Эта погрешность называется АДДИТИВНОЙ (она складывается с выходным напряжением).
Слайд 18⮚ АБСОЛЮТНАЯ ПОГРЕШНОСТЬ ПРЕОБРАЗОВАНИЯ (∆) - отклонение выходного напряжения от
номинального, соответствующего конечной точке преобразования. Измеряется "∆" в единицах младшего
разряда (е.м.р.). Эта погрешность называется МУЛЬТИ-ПЛИКАТИВНОЙ.
НЕЛИНЕЙНОСТЬ ПРЕОБРАЗО-ВАНИЯ (∆л) - отклонение реальной передаточной характеристики от идеальной. Значение нелинейности не должно выходить за пределы ± е.м.р.
Слайд 19ДИНАМИЧЕСКИЕ ПАРАМЕТРЫ Ц А П
⮚ ВРЕМЯ УСТАНОВЛЕНИЯ ВЫХОДНОГО НАПРЯЖЕНИЯ
(tуст) – интервал времени от момента подачи кода N на
вход ЦАП до момента, при котором напряжение окончательно войдет в зону шириной ±е.м.р. или другой оговоренной величины, симметрично расположенной относительно установившегося значения.
⮚ МАКСИМАЛЬНАЯ ЧАСТОТА ПРЕОБРАЗОВАНИЯ - наибольшая частота, при которой параметры ЦАП соответствуют заданным.
Слайд 20 Одним из важных параметров ЦАП является - ШУМ ПРЕОБРАЗОВАНИЯ или
ШУМ КВАНТОВАНИЯ. Уровень шума (Dш) измеряется в относительных единицах, как
отношение максимального выходного напряжения ЦАП к величине шага квантования. Обычно уровень шума измеряется в "дециБелах":
Dш = 20 * lg (Uмакс(N) / ∆ Uр.с).
Dш = 20 * lg (Nмакс) = 20 * lg (2n).
Уровни шумов квантования ЦАП
Разрядность ЦАП (бит) 6 7 8 10 12 14 16
Уровень шума (дБ) 36 42 48 60 72 84 96
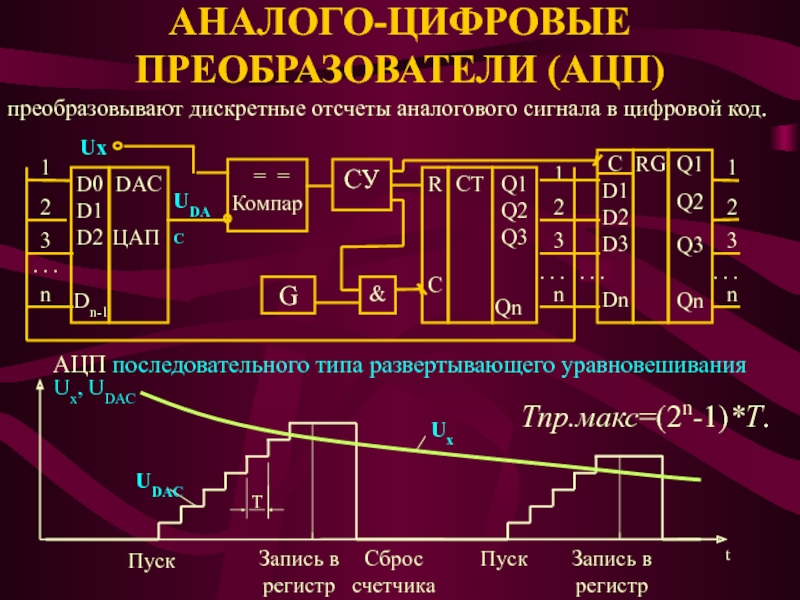
Слайд 21АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ (АЦП)
преобразовывают дискретные отсчеты аналогового сигнала в цифровой код.
АЦП последовательного типа развертывающего уравновешивания
Тпр.макс=(2n-1)*T.
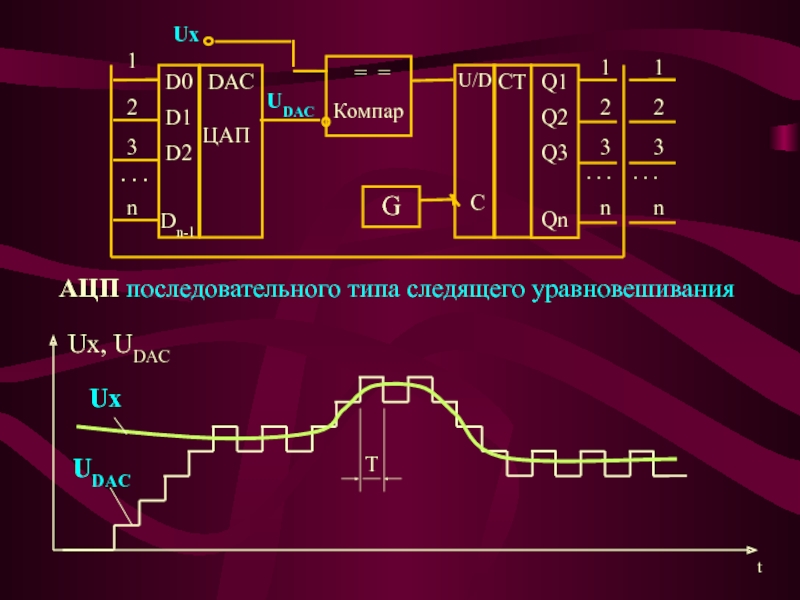
Слайд 22АЦП последовательного типа следящего уравновешивания
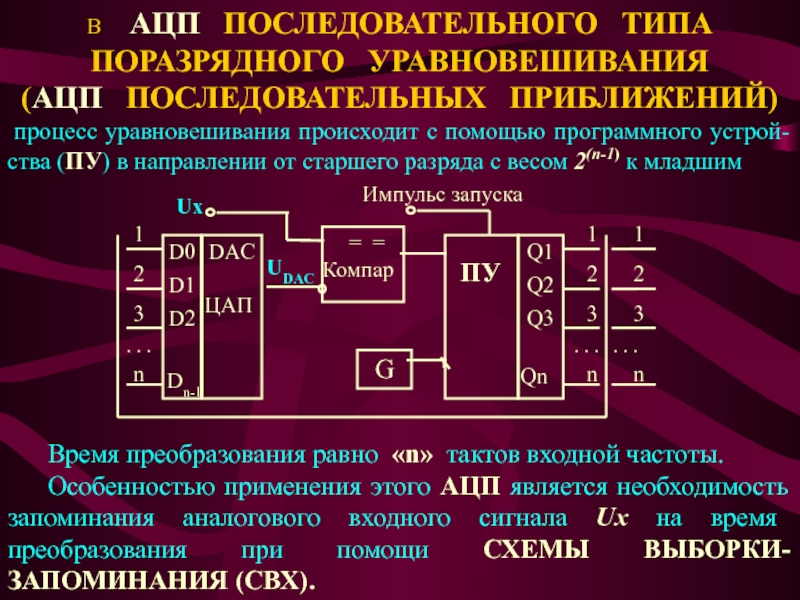
Слайд 23В АЦП ПОСЛЕДОВАТЕЛЬНОГО ТИПА ПОРАЗРЯДНОГО
УРАВНОВЕШИВАНИЯ
(АЦП ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ)
процесс уравновешивания происходит с
помощью программного устрой-ства (ПУ) в направлении от старшего разряда с весом 2(n-1) к младшим
Импульс запуска
. . .
1
2
3
n
1
2
3
n
1
2
3
n
D0
D1
D2
DAC
ЦАП
Dn-1
UDAC
Ux
. . .
G
. . .
Время преобразования равно «n» тактов входной частоты.
Особенностью применения этого АЦП является необходимость запоминания аналогового входного сигнала Ux на время преобразования при помощи СХЕМЫ ВЫБОРКИ-ЗАПОМИНАНИЯ (СВХ).
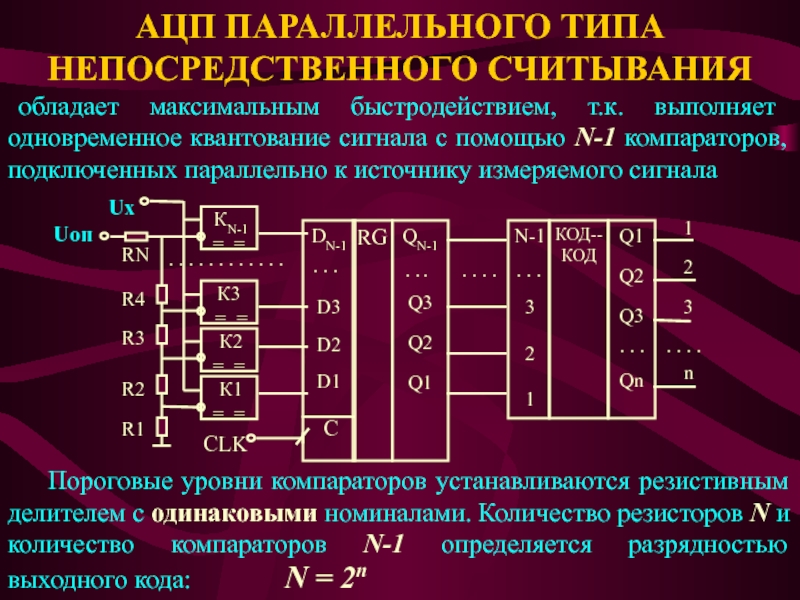
Слайд 24АЦП ПАРАЛЛЕЛЬНОГО ТИПА НЕПОСРЕДСТВЕННОГО СЧИТЫВАНИЯ
обладает максимальным быстродействием, т.к. выполняет
одновременное квантование сигнала с помощью N-1 компараторов, подключенных параллельно к
источнику измеряемого сигнала
Пороговые уровни компараторов устанавливаются резистивным делителем с одинаковыми номиналами. Количество резисторов N и количество компараторов N-1 определяется разрядностью выходного кода: N = 2n
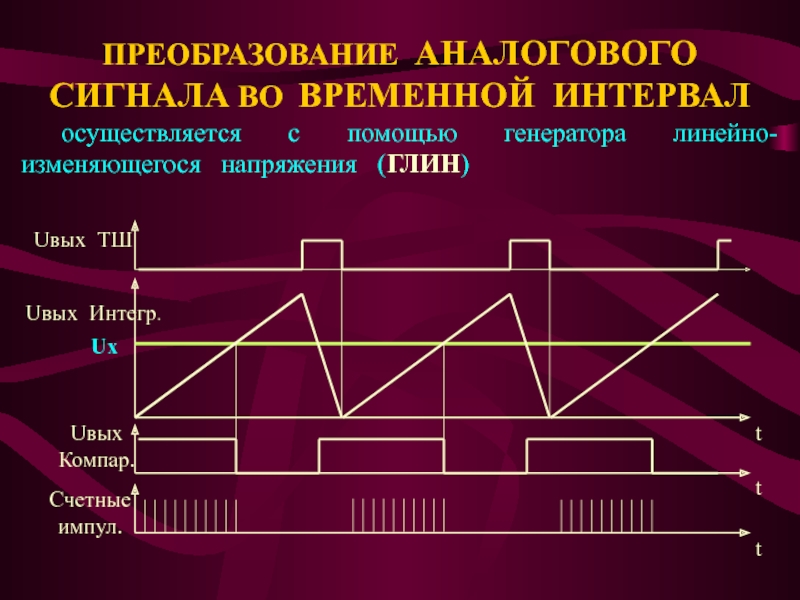
Слайд 25ПРЕОБРАЗОВАНИЕ АНАЛОГОВОГО СИГНАЛА ВО ВРЕМЕННОЙ ИНТЕРВАЛ
осуществляется с помощью генератора
линейно-изменяющегося напряжения (ГЛИН)
Слайд 26
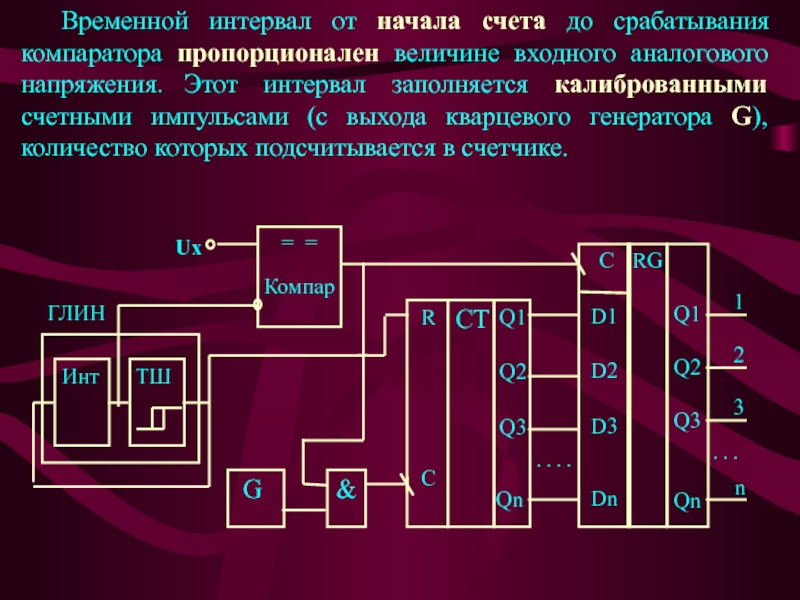
Временной интервал от начала счета до срабатывания компаратора пропорционален величине
входного аналогового напряжения. Этот интервал заполняется калиброванными счетными импульсами (с
выхода кварцевого генератора G), количество которых подсчитывается в счетчике.
Слайд 27 Алгоритм работы этой схемы аналогичен АЦП последо-вательного типа развертывающего уравновешивания.
Поэтому оба преобразователя могут использоваться для преобразования аналогового напряжения во
временной интервал.
Основным недостатком рассмотренных АЦП последо-вательного типа является их низкая помехоустойчивость от наводок питающей сети. Этот недостаток можно устранить, если в процессе преобразования использовать операцию интегрирования за фиксированный интервал времени, кратный периоду сетевого напряжения.
Такой алгоритм реализован в АЦП С ДВУХТАКТНЫМ ИНТЕГРИРОВАНИЕМ, в котором полный цикл работы состоит из двух тактов.
Слайд 28 В первом такте с помощью аналогового интегратора на операци-онном усилителе
интегри-руется входное напряжение за фиксированный интервал времени Т1. При этом
на интегрирующем конден-саторе С накапливается заряд:
T1
T2′
T2″
Uвых интегр
t
где: Ux - среднее входное напряжение за время Т1.
Во втором такте происходит разряд конденсатора от источника опорного напряжения Uоп, который имеет полярность противоположную входному напряжению, и подключается на вход интегратора с помощью аналогового ключа (АК).
Слайд 29&
. . . .
1
2
3
n
R
C
CT
Q1
Q2
Q3
Qn
. . .
G
Uоп
ОУ
СУ
АК
Uх
R
C
Импульс запуска
Этот процесс продолжается до полного разряда конденсатора, что
фиксируется компаратором. При этом удаленный из конденсатора заряд: g2=Uоп*T2/(R*C),
где: Т2 - время разряда конденсатора.
T2 = Ux * T1 / Uоп
Слайд 30ПАРАМЕТРЫ АЦП
⮚ ДИАПАЗОН ИЗМЕРЯЕМЫХ ВЕЛИЧИН - максимальное Uмакс и минимальное
Uмин для данного АЦП значения измеряемой величины.
⮚ ПОГРЕШНОСТЬ КВАНТОВАНИЯ (дискретности)
Uкв – методическая погрешность, вызываемая конечным значением шага квантования (единицей младшего разряда е.м.р.).
U кв = (Uмакс - Uмин) / (2n).
⮚ ПОГРЕШНОСТЬ СМЕЩЕНИЯ НУЛЯ (аддитивная погрешность) Uсм - характеризует параллельный сдвиг всей передаточной характеристики реального АЦП по отношению к идеальному.
⮚ ПОГРЕШНОСТЬ КОЭФФИЦИЕНТА ПЕРЕДАЧИ (мультипликативная погрешность) - величина, характеризующая отклонение крутизны усредненной передаточной характе-ристики АЦП от крутизны идеальной характеристики.
Слайд 31 ⮚ НЕЛИНЕЙНОСТЬ - отклонение передаточной характеристики АЦП во всем диапазоне изменения
входного сигнала.
⮚ ЧАСТОТА ДИСКРЕТИЗАЦИИ Fд - частота, с которой происходит образование
дискретных значений сигнала.
⮚ ВРЕМЯ ПРЕОБРАЗОВАНИЯ Тпр - время, отсчитываемое от начала преобразования до появления на выходе кода, соответствующего данной выборке.
⮚ ВРЕМЯ ВЫБОРКИ Тв - время, в течение которого происходит образование одного выбранного значения.
Слайд 32Вопросы для экспресс-контроля
1. Зачем применяется преобразование непрерыв-ных сигналов в дискретные?
2.
Назовите основные соотношения Котельникова-Найквиста при дискретизации сигнала.
3. Назовите точный метод восстановления
непре-рывного сигнала из дискретного. Привести практи-ческие примеры восстановления непрерывных сигналов из дискретных с меньшей точностью.
4. Чем определяется выбор величины шага кванто-вания непрерывных сигналов?
5. В чем отличие абсолютной погрешности кванто-вания от относительной погрешности? Величины измерения относительной погрешности.
Слайд 33Вопросы для экспресс-контроля
6. Назначение ЦАП и АЦП.
7. Преимущества ЦАП с
матрицей R-2R.
8. Какой ЦАП обладает максимальным быстро-действием? Чем достигается
максимальное быстродействие?
9. От чего зависит точность ЦАП?
10. Перечислите основные статические и динами-ческие параметры ЦАП.
11. Что такое шум квантования? Как его уменьшить?
Слайд 34ЛЕКЦИЯ ОКОНЧЕНА
СПАСИБО ЗА
ВНИМАНИЕ