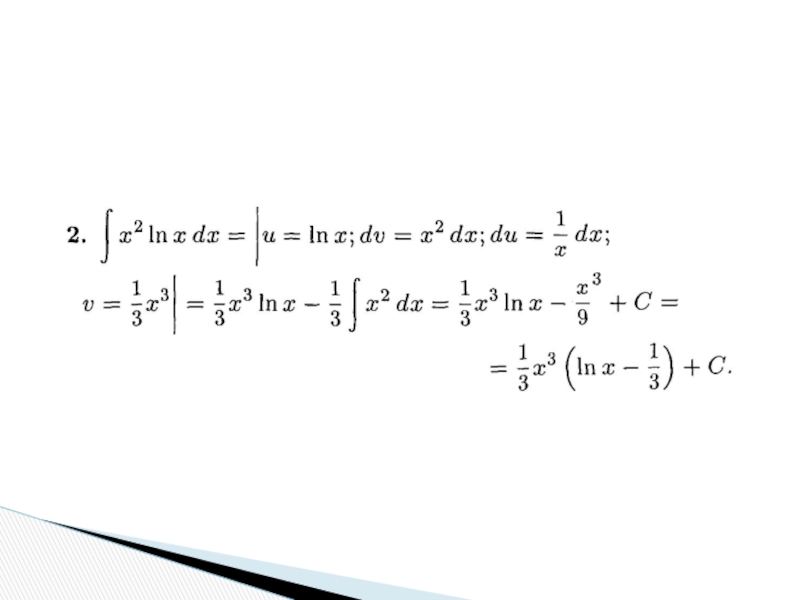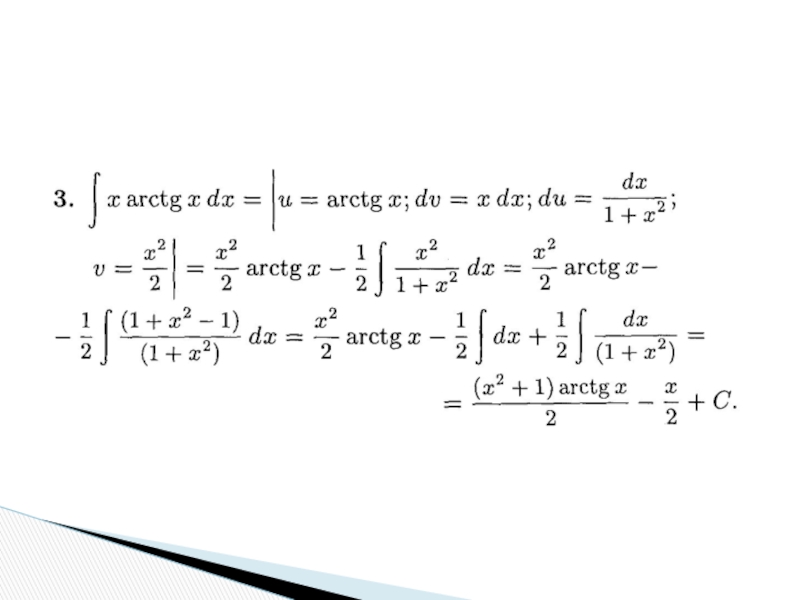Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация-Лекция 3 -математика-Фармация.pptx
Содержание
- 1. Презентация-Лекция 3 -математика-Фармация.pptx
- 2. При изучении дифференциального исчисления рассматривалась задача нахождения
- 3. Например, известна скорость перемещения точки v(t), а
- 4. Определение: Дифференцируемая функция F(x) называется первообразной для
- 5. Первообразная для заданной функции f(x) существует только,
- 6. Определение: Выражение F(x)+C, где С - произвольная
- 7. Знак ∫ - знак неопределенного интеграла;f(x)dx – подынтегральное выражение;f(x) – подынтегральная функция.
- 8. Определение: Операция нахождения первообразной по заданной производной
- 9. Придавая постоянной величине С различные значения С1,
- 10. Следовательно, геометрически неопределенный интеграл представляет собой семейство интегральных кривых.
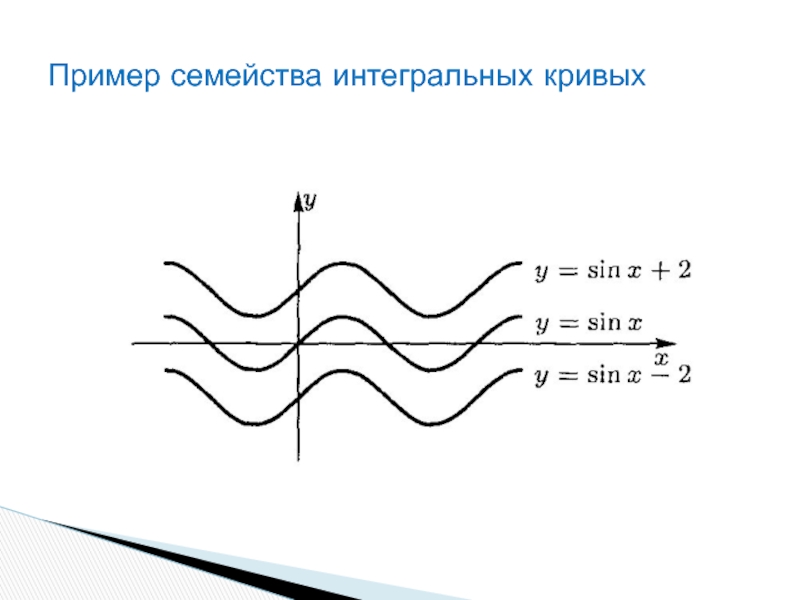
- 11. Пример семейства интегральных кривых
- 12. Чтобы находить первообразные, необходимо составить и выучить
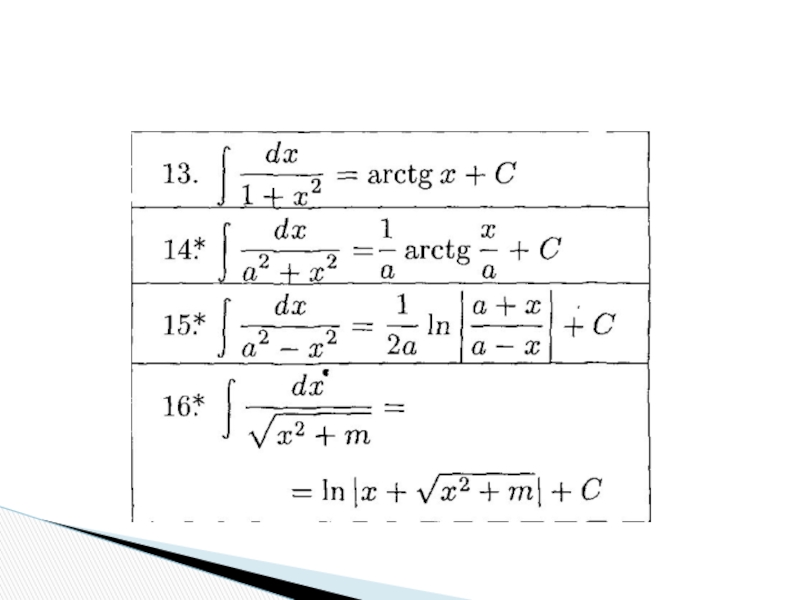
- 13. Таблица основных неопределенных интегралов
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. 1) Производная от неопределенного интеграла равна подынтегральной функции.2. Свойства неопределенных интегралов
- 18. 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
- 19. 3) Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:
- 20. 4) Постоянный множитель можно выносить за знак интеграла:
- 21. 5) Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:
- 22. Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если
- 23. Этот метод заключается в прямом использовании табличных интегралов и свойств.3. Непосредственное интегрирование
- 24. Слайд 24
- 25. Этот метод заключается в разложении подынтегральной функции
- 26. Слайд 26
- 27. Таких методов два:а) метод замены переменной;б) интегрирование по частям.3. Основные методы интегрирования
- 28. Метод основан на замене переменной в неопределенном
- 29. Пример: Найти неопределенный интеграл: ∫cos2xdxЭтот интеграл не является табличным.Произведем замену: y = 2xТогда dy=(y)’dx=2dxdx = dy/2Соответственно:
- 30. Дифференциал произведения двух функций определяется формулой:d(u•v) =
- 31. Применение этого метода требует субъективного представления подынтегрального
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Любой результат можно проверить дифференцированием.Например, в последнем случае:
- 39. Слайд 39
- 40. Слайд 40
- 41. Скачать презентанцию
При изучении дифференциального исчисления рассматривалась задача нахождения производной или дифференциала по заданной функции y=F(x), то есть нужно было найти f(x)=F’(x) или dF(x)=F’(x)dx=f(x)dx.Можно поставить обратную задачу: восстановить продифференцированную функцию, т.е., зная производную
Слайды и текст этой презентации
Слайд 1ЛЕКЦИЯ № 3
по дисциплине «Математика»
на тему: «Неопределенный интеграл»
для курсантов I
курса по военной специальности «Фармация»
медицинской физики
Слайд 2При изучении дифференциального исчисления рассматривалась задача нахождения производной или дифференциала
по заданной функции y=F(x), то есть нужно было найти f(x)=F’(x)
или dF(x)=F’(x)dx=f(x)dx.Можно поставить обратную задачу: восстановить продифференцированную функцию, т.е., зная производную f(x) или дифференциал f(x)dx, найти такую функцию F(x), чтобы F’(x) = f(x).
1. Понятие неопределенного интеграла
Слайд 3
Например, известна скорость перемещения точки v(t), а найти нужно закон
ее перемещения: S(t).
Эта задача является более трудной, чем задача дифференцирования.
Для решения подобных задач вводятся новые понятия и действия.
Слайд 4Определение: Дифференцируемая функция F(x) называется первообразной для функции f(x) на
интервале (a,b), если F’(x)=f(x) на интервале (a,b).
Например, для f(x) =x2
первообразная F(x) = x3/3, так как F’(x)=(x3/3)’=x2.
Для f(x) =cosx первообразной будет
F(x) =sinx, так как F’(x)=(sinx)’=cosx.
Слайд 5Первообразная для заданной функции f(x) существует только, если эта функция
непрерывна на (a,b).
Кроме того, первообразных – множество, и отличаются они
только постоянным слагаемым.Действительно, sinx+2, sinx-2, sinx+C – все эти функции будут являться первообразными для функции f(x) =cosx .
Слайд 6Определение: Выражение F(x)+C, где С - произвольная постоянная величина, определяющее
множество первообразных для функции f(x) называется неопределенным интегралом и
обозначается
символомт.е.
Слайд 7
Знак ∫ - знак неопределенного интеграла;
f(x)dx – подынтегральное выражение;
f(x) –
подынтегральная функция.
Слайд 8Определение: Операция нахождения первообразной по заданной производной или дифференциалу называется
интегрированием.
Интегрирование – действие, обратное дифференцированию.
Его можно проверить дифференцированием, причем
дифференцирование однозначно, а интегрирование дает ответ с точностью до постоянной.
Слайд 9Придавая постоянной величине С различные значения С1, С2, С3, получим
различные функции y1(x)=F(x)+C1, y2(x)=F(x)+C2, y3(x)=F(x)+C3, каждая из которых задает на
координатной плоскости кривую, называемую интегральной.Все графики интегральных кривых сдвинуты друг относительно друга вдоль оси OY.
Слайд 10
Следовательно, геометрически неопределенный интеграл представляет собой семейство интегральных кривых.
Слайд 12Чтобы находить первообразные, необходимо составить и выучить наизусть таблицу неопределенных
интегралов от основных элементарных функций.
Она получается в результате обращения соответствующих
формул дифференцирования.Например, если (sinx)’=cosx, то ∫cosxdx=sinx+C.
Слайд 171) Производная от неопределенного интеграла равна подынтегральной функции.
2. Свойства неопределенных
интегралов
Слайд 193) Неопределенный интеграл от дифференциала функции равен этой функции, сложенной
с произвольной постоянной:
Слайд 215) Интеграл от алгебраической суммы двух функций равен алгебраической сумме
интегралов от этих функций:
Слайд 22Формула интегрирования остается справедливой, если переменная интегрирования является функцией:
если
Слайд 23Этот метод заключается в прямом использовании табличных интегралов и свойств.
3.
Непосредственное интегрирование
Слайд 25Этот метод заключается в разложении подынтегральной функции в линейную комбинацию
более простых функций с использованием известных формул.
Метод разложения
Слайд 27
Таких методов два:
а) метод замены переменной;
б) интегрирование по частям.
3. Основные
методы интегрирования
Слайд 28Метод основан на замене переменной в неопределенном интеграле с целью
свести его нахождение к нахождению такого неопределенного интеграла, который может
быть найден методом разложения.Другими словами, необходимо получить:
∫f1(x)dx = ∫f2(y)dy, где y = φ(x)
Метод замены переменной
Слайд 29Пример: Найти неопределенный интеграл: ∫cos2xdx
Этот интеграл не является табличным.
Произведем замену:
y = 2x
Тогда dy=(y)’dx=2dx
dx = dy/2
Соответственно:
Слайд 30Дифференциал произведения двух функций определяется формулой:
d(u•v) = udv + vdu
Интегрируя это равенство, получаем:
u•v = ∫udv+∫vdu
Отсюда:
∫udv= u•v -
∫vdu Это и есть формула интегрирования по частям.
Интегрирование по частям
Слайд 31
Применение этого метода требует субъективного представления подынтегрального выражения в виде
udv, причем интеграл ∫vdu не должен быть труднее, чем интеграл
∫udv.
