Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 13.pptx
Содержание
- 1. Лекция 13.pptx
- 2. 1. Геометрические примитивы.Под геометрическими примитивами понимают тот
- 3. Такой расширенный набор примитивов связан с аппаратной
- 4. Существует альтернативное направление - конструктивная геометрией тел.
- 5. Исторически сложилось так, что первые дисплеи были
- 6. 2. Полигональные модели.Для полигональных моделей используются в
- 7. Полигон моделирует плоский объект и может описывать
- 8. Достоинства векторно-полигональной модели: удобство масштабирования объектов; небольшой объем данных
- 9. 3. Воксельные модели.Воксельная модель - это представление
- 10. Достоинства воксельной модели: возможность представлять внутренность объекта, а
- 11. Недостатки воксельной модели: большое количество информации, необходимое
- 12. 4. Функциональные модели.Характерной особенностью задания поверхностей с
- 13. Внешняя область квадрика - множество точек, удовлетворяющих
- 14. Достоинства функциональной модели: легкая процедура расчета координат каждой
- 15. 5. Системы координат: мировая, объектная, наблюдателя и
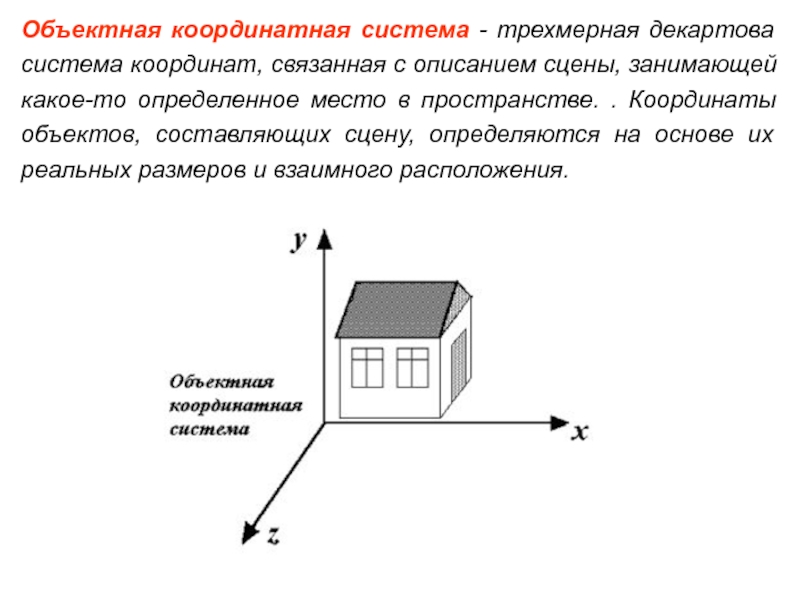
- 16. Объектная координатная система - трехмерная декартова система
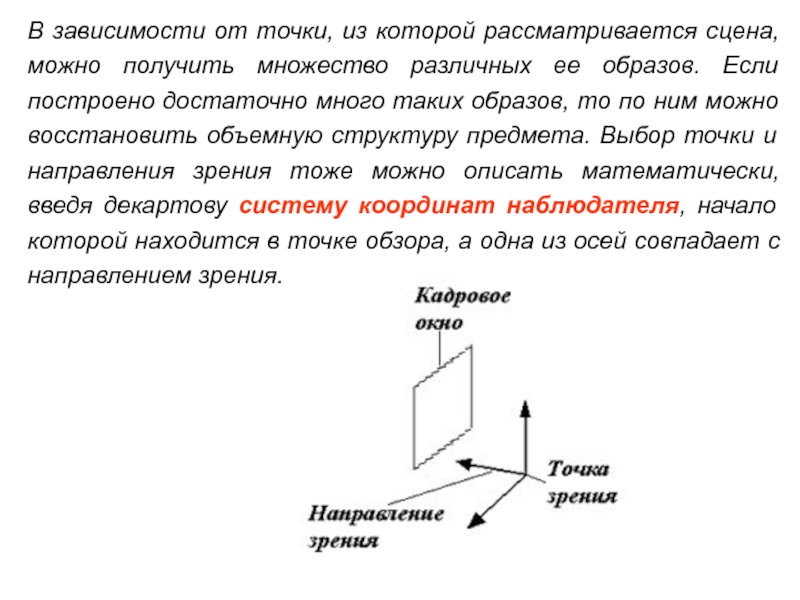
- 17. В зависимости от точки, из которой рассматривается
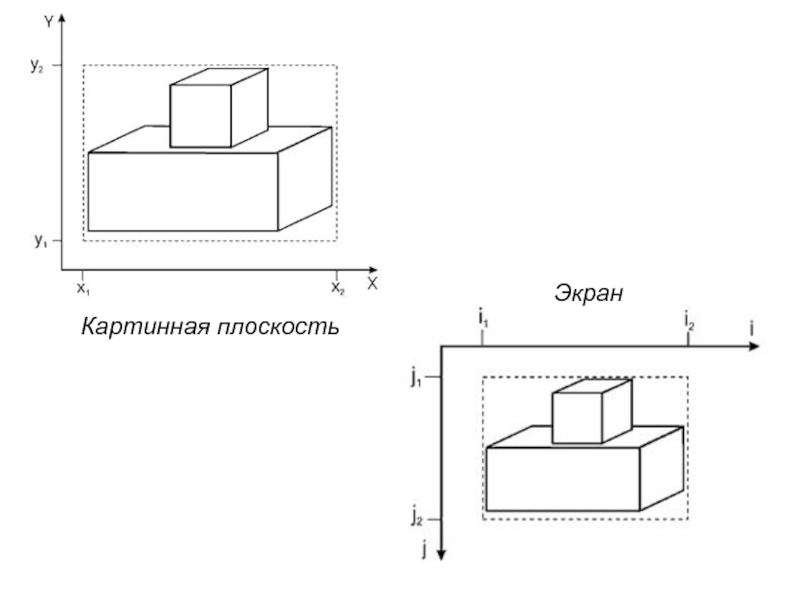
- 18. Картинная плоскость – плоскость, на которой формируется
- 19. Картинная плоскость Экран
- 20. Слайд 20
- 21. При таком отображении прямоугольная область образа в
- 22. Слайд 22
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 13.
Геометрические примитивы.
План лекции:
1. Геометрические примитивы.
2. Полигональные модели.
Слайд 21. Геометрические примитивы.
Под геометрическими примитивами понимают тот базовый набор геометрических
фигур, который лежит в основе всех графических построений, причем эти
фигуры должны образовывать "базис" в том смысле, что ни один из этих объектов нельзя построить через другие.Существует точка зрения, что базисный набор можно ограничить отрезком, многоугольником и набором литер (символов). Другая точка зрения состоит в том, что в набор примитивов необходимо включить гладкие кривые различного рода (окружности, эллипсы), некоторые классы поверхностей и даже сплошные геометрические тела.
Слайд 3Такой расширенный набор примитивов связан с аппаратной реализацией и создает
проблему перенесения программных приложений с одного компьютера на другой.
При
создании трехмерных геометрических примитивов программисты сталкиваются с проблемой их математического описания, разработки методов манипулирования такими объектами. Те типы объектов, которые не попадают в список базовых, надо уметь приближать с помощью этих примитивов.
Слайд 4Существует альтернативное направление - конструктивная геометрией тел. В системах, использующих
этот подход, объекты строятся из объемных примитивов с использованием теоретико-множественных
операций (объединение, пересечение).Система трехмерной графики OpenGL включает примитивы:
точки (вершины);
отрезки;
ломаные;
многоугольники (среди которых особо выделяются треугольники и четырехугольники);
полосы (группы треугольников или четырехугольников с общими вершинами);
шрифты.
Слайд 5Исторически сложилось так, что первые дисплеи были векторными, поэтому базовым
примитивом был отрезок.
Самая первая интерактивная программа Sketchpad А.Сазерленда в
качестве одного из примитивов имела прямоугольник, после чего этот объект уже традиционно входил в различные графические библиотеки. В систему OpenGL входят также некоторые геометрические тела: сфера, цилиндр, конус и др.
Слайд 62. Полигональные модели.
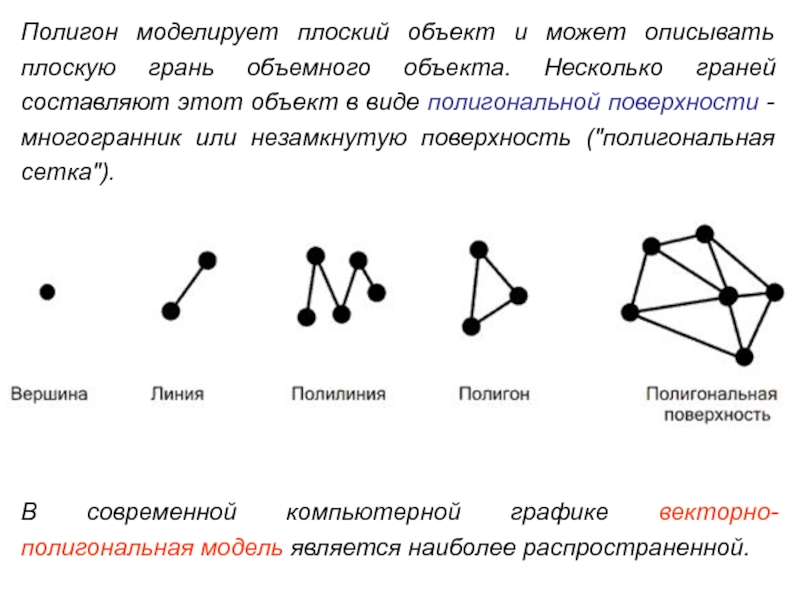
Для полигональных моделей используются в качестве примитивов вершины
(точки в пространстве), отрезки прямых (векторы), из которых строятся
полилинии,
полигоны и
полигональные поверхности.
Главным элементом описания является вершина, все остальные являются производными.
В трехмерной декартовой системе координаты вершины определяются своими координатами (x,y,z), линия задается двумя вершинами, полилиния представляет собой незамкнутую ломаную линию, полигон - замкнутую ломаную линию.
Слайд 7Полигон моделирует плоский объект и может описывать плоскую грань объемного
объекта. Несколько граней составляют этот объект в виде полигональной поверхности
- многогранник или незамкнутую поверхность ("полигональная сетка").В современной компьютерной графике векторно-полигональная модель является наиболее распространенной.
Слайд 8Достоинства векторно-полигональной модели:
удобство масштабирования объектов;
небольшой объем данных для описания простых
поверхностей;
аппаратная поддержка многих операций.
Недостатки:
алгоритмы визуализации выполнения топологических операций (например,
построение сечений) довольно сложны;аппроксимация плоскими гранями приводит к значительной погрешности, особенно при моделировании поверхностей сложной формы.
Слайд 93. Воксельные модели.
Воксельная модель - это представление объектов в виде
трехмерного массива объемных (кубических) элементов. Название "воксель" составлено из двух
слов: volume element. Так же как и пиксель, воксель имеет свои атрибуты (цвет, прозрачность и т. п.).Полная прозрачность вокселя означает пустоту в соответствующей точке объема. Чем больше вокселей в определенном объеме и меньше их размер, тем точнее моделируются трехмерные объекты.
Слайд 10Достоинства воксельной модели:
возможность представлять внутренность объекта, а не только внешний
слой; простая процедура отображения объемных сцен;
простое выполнение топологических операций; например,
чтобы показать сечение пространственного тела, достаточно воксели сделать прозрачными.Слайд 11Недостатки воксельной модели:
большое количество информации, необходимое для представления объемных
данных ;
значительные затраты памяти, ограничивающие разрешающую способность, точность моделирования;
проблемы
при увеличении или уменьшении изображения; например, с увеличением ухудшается разрешающая способность изображения.Слайд 124. Функциональные модели.
Характерной особенностью задания поверхностей с помощью поверхностей свободных
(или функциональных моделей) является то, что основным примитивом здесь является
поверхность второго порядка - квадрик. Он определяется с помощью вещественной непрерывной функции трех переменных в виде неравенства:Квадрик - это замкнутое подмножество евклидова пространства, все точки которого удовлетворяют неравенству
Граница квадрика описывается уравнением
Слайд 13Внешняя область квадрика - множество точек, удовлетворяющих неравенству
Свободная форма
- это произвольная поверхность, обладающая свойствами гладкости, непрерывности и неразрывности.
На базе квадриков строятся свободные формы, которые описывают функциональные модели.
Слайд 14Достоинства функциональной модели:
легкая процедура расчета координат каждой точки;
небольшой объем информации
для описания достаточно сложных форм;
возможность строить поверхности на основе скалярных
данных без предварительной триангуляции.Слайд 155. Системы координат: мировая, объектная,
наблюдателя и экранная.
Одной из распространенных
задач компьютерной графики является изображение двумерных графиков в некоторой системе
координат. Эти прикладные координаты позволяют задавать объекты в двумерном или трехмерном мире пользователя, и их принято называть мировыми координатами.Пространственная сцена - группы трехмерных объектов, предназначенных для изображения.
Образ - двумерное изображение пространственной сцены.