Статистическая проверка гипотез

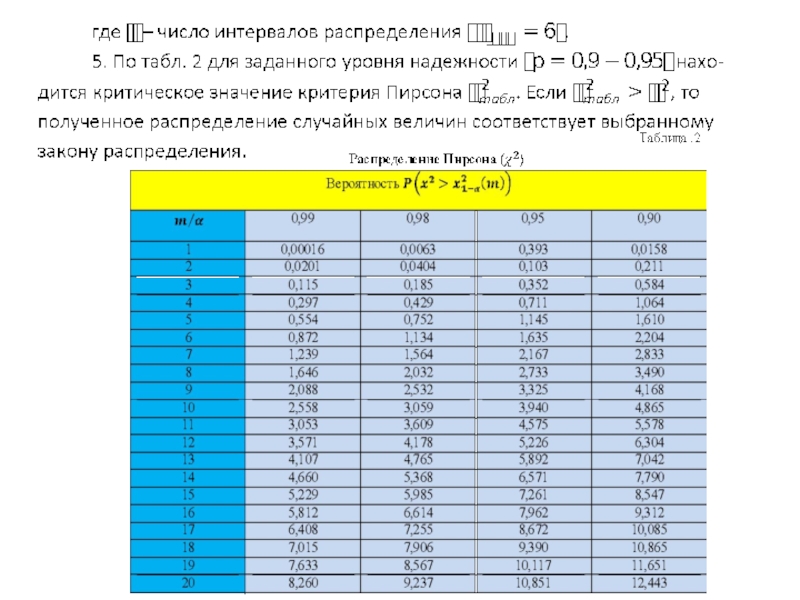
и корреляционного отношения.
Если число опытов в каждой точке эксперимента равно

единице, то значимость корреляционного отношения (η), т.е. его отличие от нуля, оценивается при помощи критерия Стьюдента по формуле:



где n – число экспериментальных точек;
n-2 – число степеней свободы;
p – уровень значимости (1 – p = q – вероятность того, что корреляционное отношение значимо отличается от нуля), обычно q = 0,95;
- табличное значение критерия Стьюдента.
Значимость коэффициентов регрессии (ai) также оценивается при помощи критерия Стьюдента:



где - дисперсия эксперимента;

- среднее квадратическое отклонение оценки коэффициента ai.

Если число опытов в каждой точке разное и равно ki , число экспериментальных точек равно (n), а общее число экспериментов во всех точках , то дисперсия эксперимента находится из формулы:

в виде


Пример: Определить значимость корреляционного отношения зависимости

, полученной после статистической обработки результатов эксперимента, приведенных в таблице 1.
Таблица 1
Критические значения критерия Стьюдента

формулы:




Табличные значения критерия Стьюдента для вероятности 95% приведены в табл.

1. При n-2=3, q = 95%, tкр< t, следовательно, корреляционное отношение значимо отличается от нуля.
Значимость коэффициентов модели « т.е. » находится из формул:






Так как табличные значения критерия Стьюдента при n – 2 = 3, q = 95%, tкр=0,873 больше, чем расчетные, то оба коэффициента значимы.