Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Закон сохранения импульса
Содержание
- 1. Закон сохранения импульса
- 2. Законы сохраненияСуществуют величины, обладающие важным свойством оставаться
- 3. Импульс частицыИмпульсом частицы (количеством движения) называется вектор,
- 4. «Импульсная» форма записи II закона НьютонаТаким
- 5. Импульс силыПусть зависимость силы от времени F(t)
- 6. Импульс системы частицРассмотрим произвольную систему частиц.Внутренние силы
- 7. Импульс системы частицПусть на каждую частицу системы
- 8. Вывод закона изменения импульса системыНайдем физическую величину,
- 9. Вывод закона изменения импульса системыПо III закону
- 10. Закон изменения импульса системы частицПроизводная по времени
- 11. Закон сохранения импульсаЗамкнутая система тел (частиц) –
- 12. Частные случаи закона сохранения импульса незамкнутой системы
- 13. Частные случаи закона сохранения импульса незамкнутой системы
- 14. Частные случаи закона сохранения импульса незамкнутой системы
- 15. ГЛАВА 3. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА3.2 Движение центра масс системы частиц
- 16. Центр масс системыРассмотрим систему частиц с массами
- 17. Свойства центра масс 1. Импульс p системы частиц
- 18. Свойства центра масс 2. Центр масс замкнутой системы
- 19. Свойства центра масс 3. Теорема о движении центра
- 20. Система центра массДля описания движения иногда удобно
- 21. Свойства системы центра масс 1. Импульс системы частиц
- 22. Свойства системы центра масс 2. Если система состоит
- 23. ГЛАВА 3. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА3.3 Движение тела с переменной массой
- 24. Уравнение МещерскогоУравнение движения тела с переменной массой
- 25. Вывод уравнения МещерскогоРассмотрим движение ракеты относительно неподвижной
- 26. Вывод уравнения МещерскогоПриращение импульсы системы «ракета -
- 27. Вывод уравнения Мещерского В этом уравнении масса является
- 28. Формула ЦиолковскогоВ качестве примера использования уравнения Мещерского
- 29. Формула ЦиолковскогоДля определения постоянной C рассмотрим начальные
- 30. Формула ЦиолковскогоФормула Циолковского позволяет оценить относительный запас
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Законы сохранения
Существуют величины, обладающие важным свойством оставаться в процессе движения
механической системы неизменными (т.е. сохраняться):
импульс
энергия
момент импульса
Законы сохранения этих величин являются
фундаментальными принципами физики(они выполняются для любых, а не только механических, систем)
Слайд 3Импульс частицы
Импульсом частицы (количеством движения) называется вектор, равный произведению массы
частицы на ее скорость:
Запишем уравнение движения частицы (II закон Ньютона
через импульс):
Слайд 4«Импульсная» форма записи
II закона Ньютона
Таким образом, производная по времени
импульса частицы равна действующей на нее силе:
Если на частицу никакие
силы не действуют, то ее импульс сохраняется:
Слайд 5Импульс силы
Пусть зависимость силы от времени F(t) известна:
Импульсом силы называется
вектор, равный произведению средней силы на промежуток времени t
ее действия:
Слайд 6Импульс системы частиц
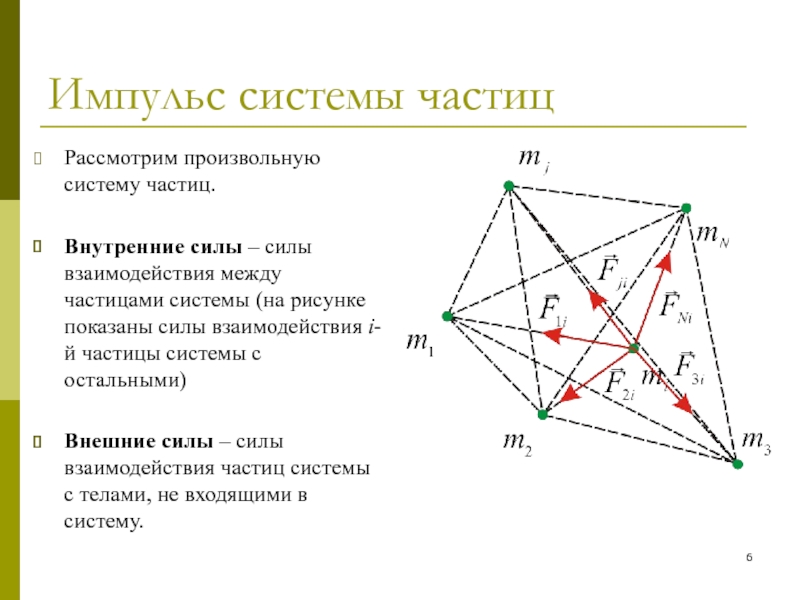
Рассмотрим произвольную систему частиц.
Внутренние силы – силы взаимодействия
между частицами системы (на рисунке показаны силы взаимодействия i-й частицы
системы с остальными)Внешние силы – силы взаимодействия частиц системы с телами, не входящими в систему.
Слайд 7Импульс системы частиц
Пусть на каждую частицу системы действуют как внутренние,
так и внешние силы.
Обозначим: i – порядковый номер частицы,
Fi внутр и Fi внеш – равнодействующие всех внутренних и внешних сил, приложенных к i-й частице системы.Импульс системы – это векторная сумма импульсов всех входящих в систему частиц:
Слайд 8Вывод закона изменения импульса системы
Найдем физическую величину, которая определяет скорость
изменения импульса системы. Для этого запишем уравнение движения i-й частицы:
Сложим
аналогичные уравнения для всех N частиц:
Слайд 9Вывод закона изменения импульса системы
По III закону Ньютона силы взаимодействия
частицы системы друг с другом попарно равны по модулю и
противоположны по направлению. Поэтому сумма всех внутренних сил равна нулю:Тогда
Слайд 10Закон изменения импульса системы частиц
Производная по времени импульса системы частиц
равна сумме всех внешних сил (т.е. изменить импульс системы могут
только внешние силы):Приращение импульса системы равно импульсу внешних сил:
Слайд 11Закон сохранения импульса
Замкнутая система тел (частиц) – система, не взаимодействующая
с внешними (не входящими в систему) телами:
Закон сохранения импульса системы:
импульс замкнутой системы частиц с течением времени не изменяется (сохраняется):
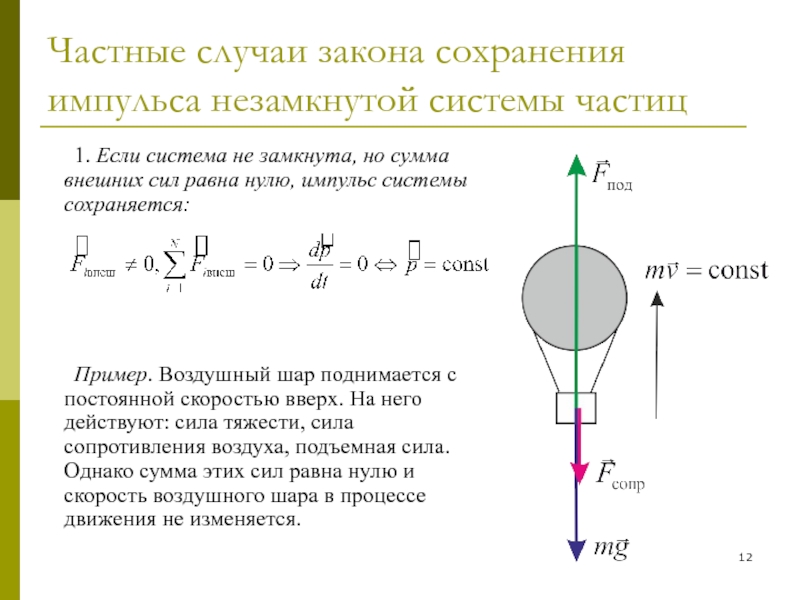
Слайд 12Частные случаи закона сохранения импульса незамкнутой системы частиц
1. Если система
не замкнута, но сумма внешних сил равна нулю, импульс системы
сохраняется:Пример. Воздушный шар поднимается с постоянной скоростью вверх. На него действуют: сила тяжести, сила сопротивления воздуха, подъемная сила. Однако сумма этих сил равна нулю и скорость воздушного шара в процессе движения не изменяется.
Слайд 13Частные случаи закона сохранения импульса незамкнутой системы частиц
2. Если проекция
на некоторое направление суммы внешних сил равна нулю, проекция на
это же направление импульса системы сохраняется:Пример. Тело массой m брошено с начальной скоростью v0 под углом α к горизонту. Если пренебречь сопротивлением воздуха, то проекция на горизонтальную ось X действующей на тело внешней силы – силы тяжести – равна нулю. Проекция на ось X импульса тела, равна в начальный момент движения mv0cosα = const в любой момент полета.
Слайд 14Частные случаи закона сохранения импульса незамкнутой системы частиц
3. Импульс системы
приблизительно сохраняется, если ограниченная по модулю внешняя сила действует в
течение очень короткого промежутка времени:Пример. Во время взрыва в воздухе снаряда на него действует внешняя сила – сила тяжести. Время взрыва мало, так что импульсом силы тяжести можно пренебречь. Следовательно, импульс снаряда непосредственно перед взрывом равен суммарному импульсу его осколков сразу после взрыва.
Слайд 16Центр масс системы
Рассмотрим систему частиц с массами m1, m2, …,
mi, …, mN. Пусть положения частиц в пространстве заданы радиусами-векторами
r1, r2, …, ri, …, rN.Центром масс (центром инерции) системы частиц называется точка C в пространстве, положение которой определяется радиусом-вектором:
Слайд 17Свойства центра масс
1. Импульс p системы частиц равен произведению массы
m системы на скорость vC ее центра масс:
Доказательство:
Слайд 18Свойства центра масс
2. Центр масс замкнутой системы частиц движется равномерно
и прямолинейно (или покоится).
Доказательство: если система замкнута, то p =
const, следовательно, из первого свойства следует, что vС = const.Слайд 19Свойства центра масс
3. Теорема о движении центра масс. Центр масс
системы частиц движется как материальная точка, в которой заключена масса
всей системы, и к которой приложена сила, равна сумме всех внешних сил:Здесь Fвнеш – сумма всех внешних сил, приложенных ко всем частицам системы.
Слайд 20Система центра масс
Для описания движения иногда удобно использовать систему отсчета,
в которой центр масс покоится.
Системой центра масс называется жестко связанная
с центром масс система отсчета, которая движется поступательно по отношению к инерциальной системе отчета.Слайд 21Свойства системы центра масс
1. Импульс системы частиц в системе центра
масс равен нулю:
Доказательство. Поскольку в системе центра масс скорость центра
масс равна нулю, vC = 0, то в соответствии со вторым свойством центра масс, p = mvC = 0.
Слайд 22Свойства системы центра масс
2. Если система состоит из двух частиц,
то их импульсы p1 и p2 в системе центра масс
равны по величине и противоположны по направлению:Доказательство. Импульс системы частиц в системе центра масс равен нулю:
Слайд 24Уравнение Мещерского
Уравнение движения тела с переменной массой было впервые получено
русским механиком И.В. Мещерским (1859 – 1935), и носит его
имя. Выведем его на примере движения ракеты.Принцип действия ракеты: ракета с большой скоростью выбрасывает вещество (газообразные продукты сгорания топлива), которое с силой воздействует на ракету и сообщает ей ускорение. Пусть на ракету действует внешняя сила F (это может быть сила тяготения, сила сопротивления среды, в которой движется ракета и т.д.)
Слайд 25Вывод уравнения Мещерского
Рассмотрим движение ракеты относительно неподвижной системы отсчета.
Пусть в
момент времени t m(t) – масса ракеты, v(t) – ее
скорость, mv(t) – импульс ракеты.Спустя промежуток времени dt: масса и скорость ракеты получат приращения dm и dv, при этом dm < 0, т.к. масса ракеты уменьшается за счета сгорания топлива.
Импульс ракеты станет равным (m + dm)(v + dv).
Импульс образовавшихся за промежуток времени dt газов равен dmгvг, где dmг – масса газов, vг – скорость газов в неподвижной системе отсчета.
Масса образовавшихся газов равна убыли массы ракеты: dmг = – dm.
Слайд 26Вывод уравнения Мещерского
Приращение импульсы системы «ракета - топливо» за промежуток
времени dt:
Раскроем скобки и пренебрежем малой величиной dmdv, заменим dmг
на –dm, тогда получим:Обозначим u = vг – v – относительная скорость истечения газов из ракеты; разделим обе части уравнения на dt
Слайд 27Вывод уравнения Мещерского
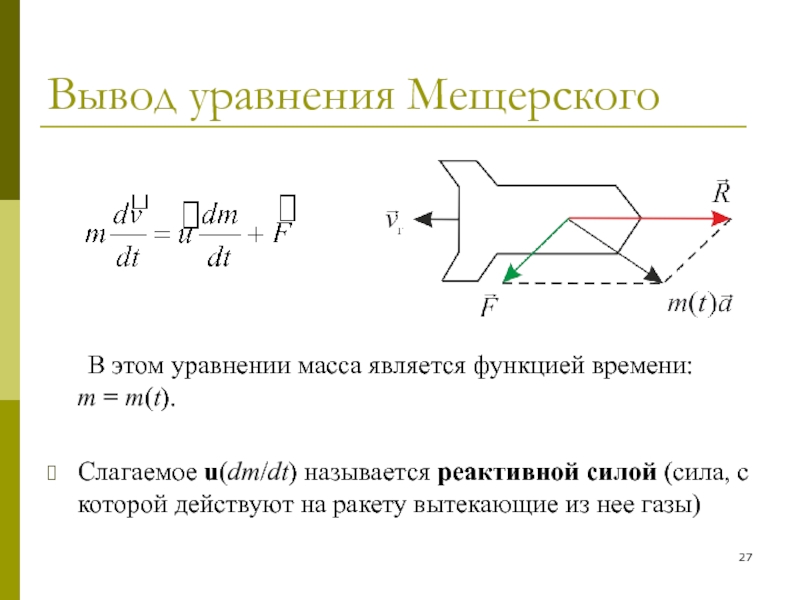
В этом уравнении масса является функцией времени:
m = m(t).
Слагаемое u(dm/dt) называется реактивной силой (сила,
с которой действуют на ракету вытекающие из нее газы)
Слайд 28Формула Циолковского
В качестве примера использования уравнения Мещерского применим его к
движению ракеты, на которую внешние силы не действуют (F =
0):Пусть ракета движется прямолинейно. Учтем, что u↑↓v, тогда уравнение примет вид:
Слайд 29Формула Циолковского
Для определения постоянной C рассмотрим начальные условия: m(t =
0) = m0 – начальная масса ракеты, когда ее скорость
равна нулю: v(t = 0) = 0. Тогда C = m0.Формула Циолковского: