Эффект Джозефсона

единой комплексной волновой функцией – параметром порядка:
Ψ=Ψ(r,t)=Ψ⋅eiχ (1.1)
2. |Ψ| – энергия

связи пар. Иногда обозначают, как |Δ|; Δ=Δ(r,t).
3. χ – фаза параметра порядка.
4. |Ψ| и χ=f(r, t)
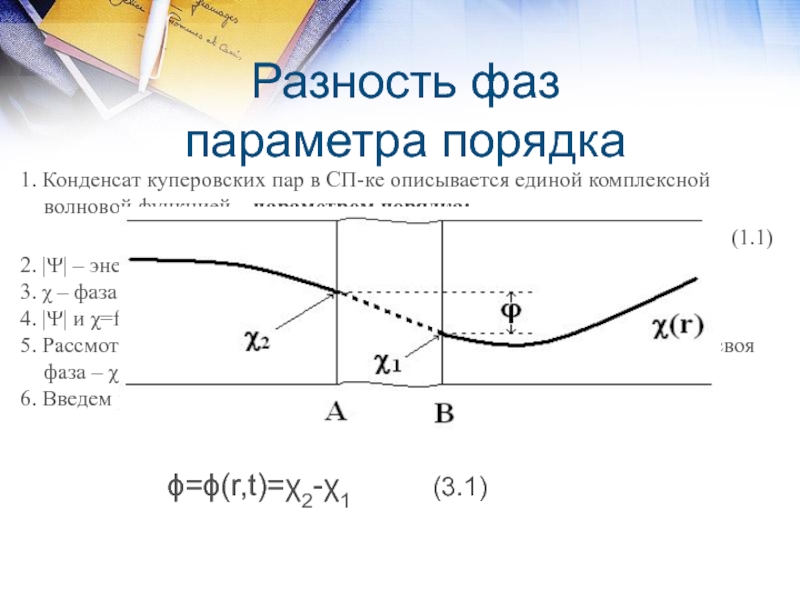
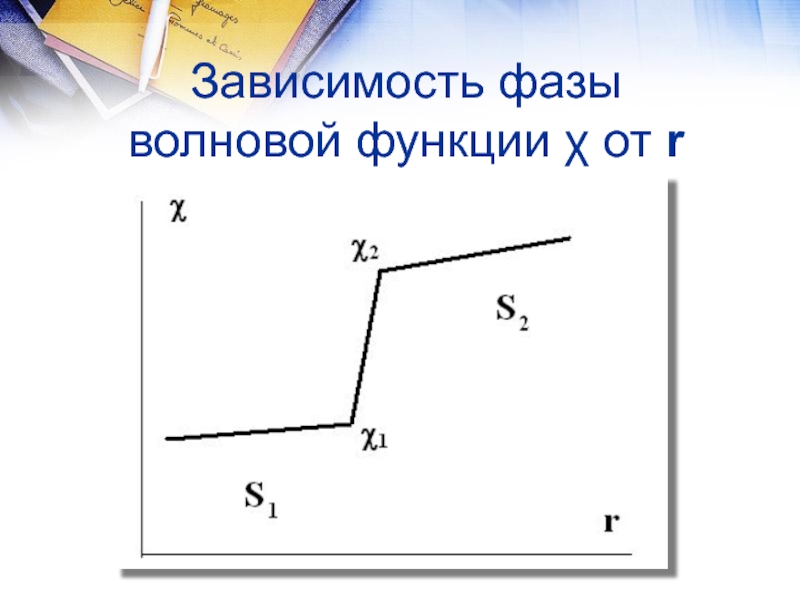
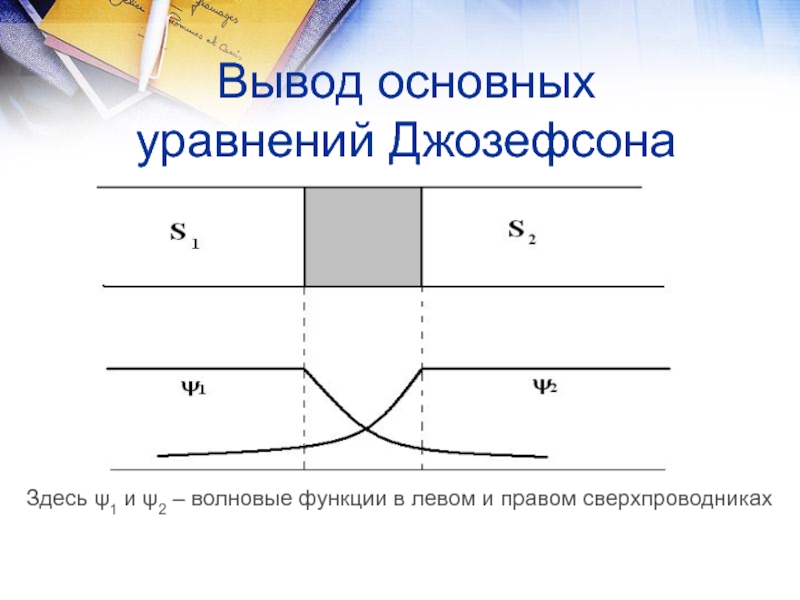
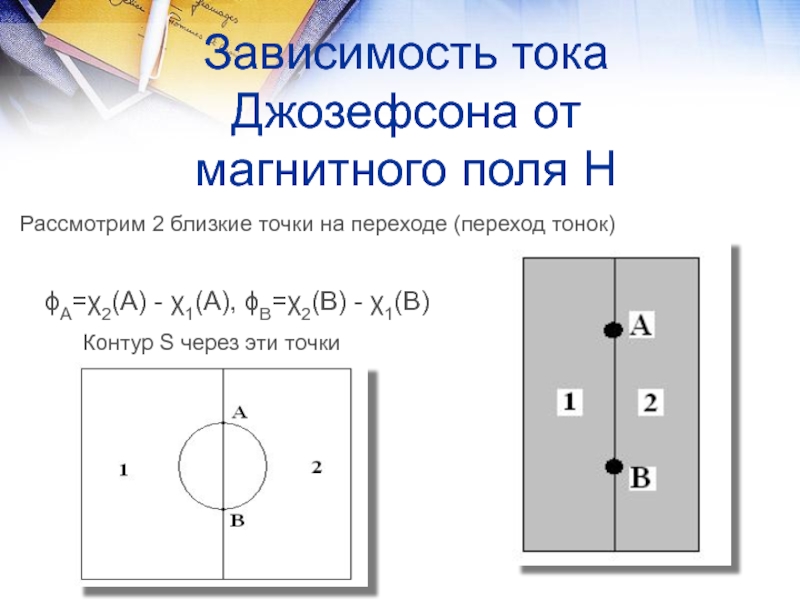
5. Рассмотрим контакт двух сверхпроводников. Как мы знаем, у каждого своя фаза – χ1, χ2.
6. Введем разность фаз эти двух сверхпроводников на их границах

ϕ=ϕ(r,t)=χ2-χ1 (3.1)

ток проходит через тонкий слой диэлектрика (d < ξ, λ),

разделяющего 2 сверхпроводника, без затухания

Второе свойство:

Существует критический ток Джозефсона Ic. Это максимальный ток, при котором еще нет затухания в барьере (диэлектрике).
Этот ток называют еще критический ток слабой связи

в сверхпроводнике определяется как
j=(e∇/2m)Ns∇χ (3.2)
Здесь ∇=∂/∂r (градиент),

Ns – концентрация «сверхпроводящих» электронов.
Это выражение следует из общего квантовомеханического выражения
j~ψ∇ψ*-ψ*∇ψ
при ψ=|ψ|eiχ, если |ψ|=√ρ не меняется

2) Т.е. χ меняется в сверхпроводнике вдоль тока. И ∇χ≠0

в левом и правом сверхпроводниках

одной стороне перехода зависит от мгновенных значений волновых функций по

обе стороны перехода. Т.е., например, ∂ψ1/∂t~αψ1+βψ2, причем β<<α.
Таким образом
i∇∂ψ1/∂t=E1ψ1+Kψ2 ⎞
i∇∂ψ2/∂t=E2ψ2+Kψ1 ⎠ (3.3)
Замечания:
1. Написаны уравнения Шредингера.
2. Е1, Е2 – собственные значения энергий (энергии основного состояния).
3. ψ1, ψ2 – это амплитуды (комплексные) волновой функции=амплитуды вероятностей. 4. K – константа связи, характеризующая переход.
1) K=0, то сверхпроводники никак не связаны и (3.3) – обычное уравнение Шредингера для одной частицы.
2) Если у нас есть связь, и она слабая, то K≠0 и K<

Т.е. V≠0 на переходе.
2. Энергетическая схема такого перехода:
И из (3.3)

имеем
i∇∂ψ1/∂t=eVψ1+Kψ2 ⎞
i∇∂ψ2/∂t=-eVψ2+Kψ1 ⎠ (3.4)
Это уточнение (3.3)

Здесь ϕ=χ2-χ1

числа частиц (пар)
j=jcsinϕ
(3.7)
Основное уравнение Джозефсона для тока:
jc=jJ=2Kρ/ħ
Для рассмотренной модели (слабая

связь с коэффициентом К) :

Величина К зависит от свойств обоих сверхпроводников и геометрии (толщины изолятора)

следует
(при равных справа числах ρ1 и ρ2):


Второе фундаментальное уравнение,

уравнение для фазы:

Итак, (3.7) и (3.8) – основные соотношения для перехода Джозефсона.

(3.8)

t, т.е., например, ϕ≠ϕ(t).
2. В ур-нии для тока (3.7) нет

времени явно, оно остается:
j=jcsinϕ
Или I=Icsinϕ.
3. А из выражения (3.8) следует
V=0,
ϕ=Const.
Эта система уравнений (3.9) и есть
основные уравнения стационарного эффекта Джозефсона

(3.9)

т.е. короткая слабая связь)
I≡IS=Icsinϕ
где Ic=Co(T)

=(при |ρ1|=|ρ2|)=Co(T)⋅

Здесь Co(T) – некоторая «постоянная» (зависящая от Т), произведение σN⋅RN – не зависит от RN, а лишь от геометрии мостика, т.к. RN~1/σN (RN-сопротивление мостика в N-состоянии, σN-удельная проводимость)

дает:
Со=

Ic=

Я заменил ρ=|Ψ|2=Δ2. Вблизи Тс величина Δ2(Т)=

Здесь ζ(х)=

- дзета-функция Римана, ζ(3)=1,202…

Т.е. вблизи Тс

Ic≈635⋅ мкА (Т в градусах К, RN в Омах).

При Тс-Т=1 К и RN=1 Ом Ic≈600 мкА

Н ток в сверхпроводнике
j=(e/m){(iħ/2)(Ψ▽Ψ*-Ψ*▽Ψ)-(2e/c)A|Ψ|2} (3.10)
B=rotA, A-векторный потенциал, 2е-заряд «частицы».
2. Ψ=

⋅еiχ, ρ≠ρ(r).
Подставим в (3.10). Появится ▽χ. Определим тогда из (3.10) этот градиент фазы:
▽χ=(2e/ħc){A+(mc/2e2ρ)j} (3.11)
3. Рассмотрим переход S-I-S

у, т.е. Ву≠0, Bx=Bz=0. Оно сосредоточено в переходе

на переходе (переход тонок)
ϕА=χ2(А) - χ1(А), ϕВ=χ2(В) - χ1(В)
Контур S

через эти точки

S

(3.12)

(3.13)

в контуре S
(3.14)

Действительно, j2-j1=δj, δj⋅dl-второй порядок малости
Из (3.12)-(3.15) получим
δϕ=(2е/ħс)δФ
где δФ=By⋅d⋅δx,
δx=xA-xB

– расстояние между точками А и В,
d=do+λ1+λ2,
do – толщина изолятора, λ1, λ2 – глубины проникновения поля в СП-и.
Поле проникает и в металл!

получим
dϕ/dx=(2ed/ ħс)By. (3.16)
Т.е. δϕ~B, т.е. магнитному полю. Очень важный результат
Проинтегрируем (3.16)

по х:
ϕ=(2ed/ ħс)By⋅x+ϕo. (3.17)
Здесь ϕo=Const, это фаза в точке, принятой нами за начало отсчета.
 
Вывод: поскольку j=jcsinϕ, то при наличии поля плотность тока разная в разных точках перехода (ϕ=ϕ(х))

ток через переход:

Здесь: начало интегрирования в центре, dx⋅dy – элемент

площади, By≠0, ϕ=ϕ(x) – см. (3.17), jc – максимальная плотность тока без поля

(3.18)

максимальный ток как Im. Это критический ток, но в поле

Н≠0. Из (3.18) находим

Ф=Byaxd

А Фо=hc/2e=2.07⋅10-7 Гс⋅см2 (CGSM)

Ic=jc⋅ax⋅ay- максимальный ток без поля

от поля (потока в переходе)

что только Ву≠0, а Вх=0

переходе-диэлектрике μ=1);
d=do+λ1+λ2 – «эффективная» толщина барьера.
3) В диэлектрике-переходе справедливы уравнения

Максвелла:
rotH = (4π/c)j + (1/c)∂D/∂t (3.21)
Сейчас мы пренебрежем емкостью перехода, и значит токами смещения ∂D/∂t.
Для принятой геометрии (3.21) будет
dHy/dx = (4π/c)jz
Полная производная, т.к. у нас только Ну≠0

Сюда подставим Ну из (3.20)
(ħс2/8πed)d2ϕ/dx2 = jz = jcsinϕ

Вообще-то и Нх≠0, поэтому в общем случае в (3.22) должен

быть и член d2ϕ/dу2

(3.22)

(3.23)

(3.22А)

Это уравнение Феррела-Прейнджа

и создаваемые ими поля Н малы), то (3.22) будет:

Решение этого

уравнения (за начало координат возьмем точку с максимальным током):
ϕ=ϕоexp(-x/λJ) (3.24)
Здесь ϕо-фаза в начале координат (где ток максимален).

Видно, что ток экспоненциально затухает с ростом х. Т.е. λJ-это глубина проникновения Джозефсоновских токов в большой переход

λJ=0.5мм (типично 0.1-1мм)