Булевы функции

Содержание

1. Булевы функции
2. 4.1 Способы задания булевой функцииПусть х1, х2, ... , хn – некоторые
3. При фиксации значений всех переменных получается набор
4. Задание булевой функции f на булевом пространстве
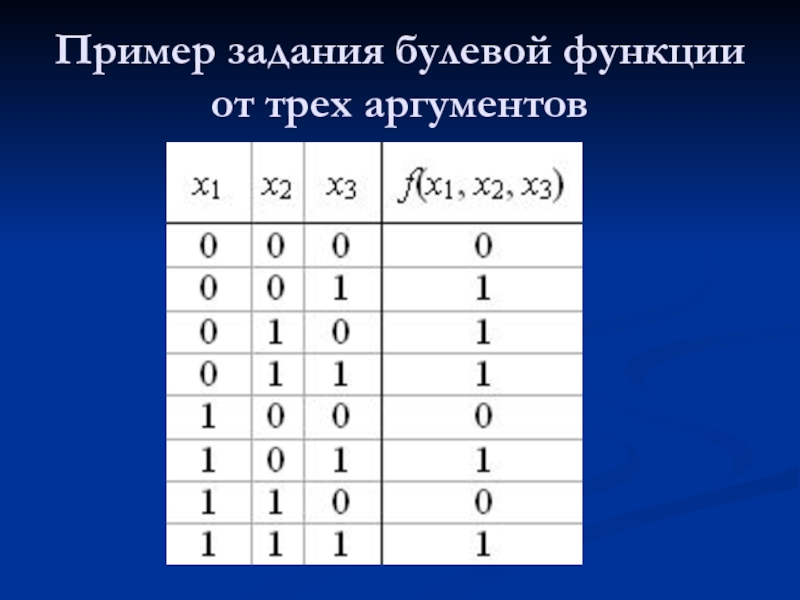
5. Пример задания булевой функции от трех аргументов
6. Для задания булевой функции можно ограничиться перечислением
7. Компактность представления характеристического множества Mf1 можно повысить,
8. Булевы векторы а = (а1, а2, … , аn) и b = (b1, b2, … , bn) находятся в
9. Троичная матрица эквивалентна булевой матрице, получаемой из
10. Такой способ задания булевой функции называют еще
11. Векторное задание булевой функции представляет собой булев
12. Если значения булевой функции определены для всех
13. 4.2 Элементарные булевы функции и алгебраические формы Рассматривая
14. Функция f(х1, х2, ... , хn) существенно зависит от аргумента хi,
15. Элементарными булевыми функциями являются функции от одной
16. Функция f1 также является тривиальной, любое ее
17. В таблице приведены все булевы функции fi (х1, х2)
18. Продолжение таблицы
19. Слайд 19
20. Слайд 20
21. Слайд 21
22. Слайд 22
23. Слайд 23
24. Слайд 24
25. Слайд 25
26. Слайд 26
27. Слайд 27
28. Слайд 28
29. Слайд 29
30. Слайд 30
31. Слайд 31
32. Слайд 32
33. Слайд 33
34. Слайд 34
35. Слайд 35
36. Слайд 36
37. Слайд 37
38. Скачать презентанцию

4.1 Способы задания булевой функцииПусть х1, х2, ... , хn – некоторые булевы переменные, т. е. переменные, принимающие значение из множества {0, 1}. Упорядоченную совокупность булевых переменных (х1, х2, ... , хn) можно рассматривать как n‑компонентный булев вектор х. Число компонент вектора

Слайды и текст этой презентации

Слайд 1Тема 4. Булевы функции

Слайд 24.1 Способы задания булевой функции
Пусть х1, х2, ... , хn – некоторые булевы переменные, т. е.

переменные, принимающие значение из множества {0, 1}. Упорядоченную совокупность булевых переменных

(х1, х2, ... , хn) можно рассматривать как n‑компонентный булев вектор х. Число компонент вектора определяет его длину, или размерность.

4.1 Способы задания булевой функцииПусть х1, х2, ... , хn – некоторые булевы переменные, т. е. переменные, принимающие значение из множества {0, 1}. Упорядоченную

Слайд 3При фиксации значений всех переменных получается набор значений переменных (х1, х2, ..., хn),

задаваемый булевым вектором длины n, состоящим из констант 0 и

1. Очевидно, 2n – число всех таких векторов. Они образуют булево пространство. Булевой функцией называется функция f : {0, 1}n → {0, 1}. Областью определения булевой функции является булево пространство М = {0, 1}n, областью значений – множество {0, 1}.

При фиксации значений всех переменных получается набор значений переменных (х1, х2, ..., хn), задаваемый булевым вектором длины n, состоящим из

Слайд 4Задание булевой функции f на булевом пространстве М делит его

на две части: Mf1 – область, где функция принимает значение

1, и Mf0 – область, где функция принимает значение 0. Множество Mf1 называется характеристическим множеством функции f.
Универсальным способом задания для любой дискретной функции является табличный способ. Таблица, представляющая функцию и называемая таблицей истинности, имеет два столбца. В левом столбце перечислены все наборы значений аргументов, в правом столбце – соответствующие им значения функции.

Задание булевой функции f на булевом пространстве М делит его на две части: Mf1 – область, где

Слайд 5Пример задания булевой функции от трех аргументов

Слайд 6Для задания булевой функции можно ограничиться перечислением элементов ее характеристического

множества Mf1. Множество Mf1 задается булевой матрицей, строки которой представляют

элементы этого множества.
Матрица является матричным способом представления булевой функции:

Для задания булевой функции можно ограничиться перечислением элементов ее характеристического множества Mf1. Множество Mf1 задается булевой матрицей,

Слайд 7Компактность представления характеристического множества Mf1 можно повысить, используя троичные векторы,

компоненты которых могут принимать в качестве своих значений кроме символов

0 и 1 также символ «–». В этом случае значения булевой функции будут задаваться не на отдельных элементах, а на интервалах пространства переменных х1, х2, ..., хn. Чтобы определить понятие интервала булева пространства, введем отношение ≤ на множестве булевых векторов.

Компактность представления характеристического множества Mf1 можно повысить, используя троичные векторы, компоненты которых могут принимать в качестве своих

Слайд 8Булевы векторы а = (а1, а2, … , аn) и b = (b1, b2, … , bn) находятся в отношении ≤ (а ≤ b)

и говорят, что а меньше b, если аi ≤ bi для любого

i = 1, 2, … , n, в противном случае они несравнимы. При этом считается, что 0 ≤ 1. Интервалом булева пространства называется множество векторов, среди которых есть минимальный и максимальный векторы, а также все векторы, меньшие максимального и большие минимального. Интервал представляется троичным вектором, который задает множество всех булевых векторов, получаемых заменой символа «–» на 1 или 0.

Булевы векторы а = (а1, а2, … , аn) и b = (b1, b2, … , bn) находятся в отношении ≤ (а ≤ b) и говорят, что а меньше b, если

Слайд 9Троичная матрица эквивалентна булевой матрице, получаемой из нее заменой каждой

троичной строки на представляемую ею совокупность булевых строк с последующим

устранением повторяющихся строк. Приведенная выше булева матрица оказывается эквивалентной троичной матрице, которая представляет ту же булеву функцию f (x1, x2, x3).

Троичная матрица эквивалентна булевой матрице, получаемой из нее заменой каждой троичной строки на представляемую ею совокупность булевых

Слайд 10Такой способ задания булевой функции называют еще интервальным. Представление булевой

функции троичной матрицей не однозначно, т. е. для одной и той

же булевой матрицы существует в общем случае не одна эквивалентная ей троичная матрица.
Две троичные матрицы эквивалентны, если они эквивалентны одной и той же булевой матрице, т. е. если они представляют одну и ту же булеву функцию.

Такой способ задания булевой функции называют еще интервальным. Представление булевой функции троичной матрицей не однозначно, т. е. для

Слайд 11Векторное задание булевой функции представляет собой булев вектор, компоненты которого

соответствуют наборам значений аргументов. Эти наборы упорядочиваются обычно согласно порядку

чисел, двоичные коды которых они представляют. Рассмотренная выше булева функция f(x1, x2, x3) представляется вектором (0 1 1 1 0 1 0 1), показывающим, что функция принимает значение 0 на наборах (0 0 0), (1 0 0), (1 1 0) и значение 1 на наборах (0 0 1), (0 1 0), (0 1 1), (1 0 1), (1 1 1)

Векторное задание булевой функции представляет собой булев вектор, компоненты которого соответствуют наборам значений аргументов. Эти наборы упорядочиваются

Слайд 12Если значения булевой функции определены для всех 2n наборов значений

вектора x, она называется полностью определенной, в противном случае –

не полностью определенной, или частичной. Задание не полностью определенной булевой функции f разбивает булево пространство на три множества: кроме Mf1 и Mf0 в нем присутствует множество Mf –, где значения функции f не определены. Для задания частичной булевой функции необходимо задать не менее двух множеств. Обычно это Mf1 и Mf0 .

Если значения булевой функции определены для всех 2n наборов значений вектора x, она называется полностью определенной, в

Слайд 134.2 Элементарные булевы функции и алгебраические формы
Рассматривая векторную форму задания

булевой функции, легко определить число булевых функций от n переменных

– это число всех 2n-компонентных булевых векторов, т. е. . Однако это число учитывает также функции и от меньшего числа аргументов. Любую функцию от n аргументов можно считать функцией от большего числа аргументов. Для этого вводится понятие существенной зависимости и несущественной зависимости.

4.2 Элементарные булевы функции и алгебраические формы Рассматривая векторную форму задания булевой функции, легко определить число булевых функций

Слайд 14Функция f(х1, х2, ... , хn) существенно зависит от аргумента хi, если
f(х1, х2, ... , хi -1, 0, хi + 1, … , хn) ≠
≠

f(х1, х2, ... , хi – 1, 1, хi + 1, … , хn).
Переменная хi в этом случае называется существенным аргументом. В противном

случае она является несущественным или фиктивным аргументом.

Функция f(х1, х2, ... , хn) существенно зависит от аргумента хi, еслиf(х1, х2, ... , хi -1, 0, хi + 1, … , хn) ≠ ≠ f(х1, х2, ... , хi – 1, 1, хi + 1, … , хn).Переменная хi в этом случае называется существенным

Слайд 15Элементарными булевыми функциями являются функции от одной и двух переменных.

Число функций от одной переменной равно 221= 4. Эти функции представлены

в таблице.

Две из них, f0 и f3, являются константами 0 и 1, переменная x для них является несущественным аргументом

Элементарными булевыми функциями являются функции от одной и двух переменных. Число функций от одной переменной равно 221= 4.

Слайд 16Функция f1 также является тривиальной, любое ее значение совпадает со

значением аргумента: f1(x) = x. Нетривиальной функцией является функция f2(x) =x, называемая отрицанием,

или инверсией.

Функция f1 также является тривиальной, любое ее значение совпадает со значением аргумента: f1(x) = x. Нетривиальной функцией является функция

Слайд 17В таблице приведены все булевы функции fi (х1, х2) от двух аргументов.

В левом столбце показаны их выражения в терминах нескольких функций,

принятых за основные.

В таблице приведены все булевы функции fi (х1, х2) от двух аргументов. В левом столбце показаны их выражения в

Разделы презентаций