Избирательные системы

Избирательная система в широком смысле –
это совокупность общественных отношений

как урегулированных, так и неурегулированных нормами права, посредством которых формируются органы законодательной, исполнительной и судебной власти.
Избирательная система в узком смысле –
это способ распределения депутатских мандатов между кандидатами в зависимости от результатов голосования избирателей.

систем
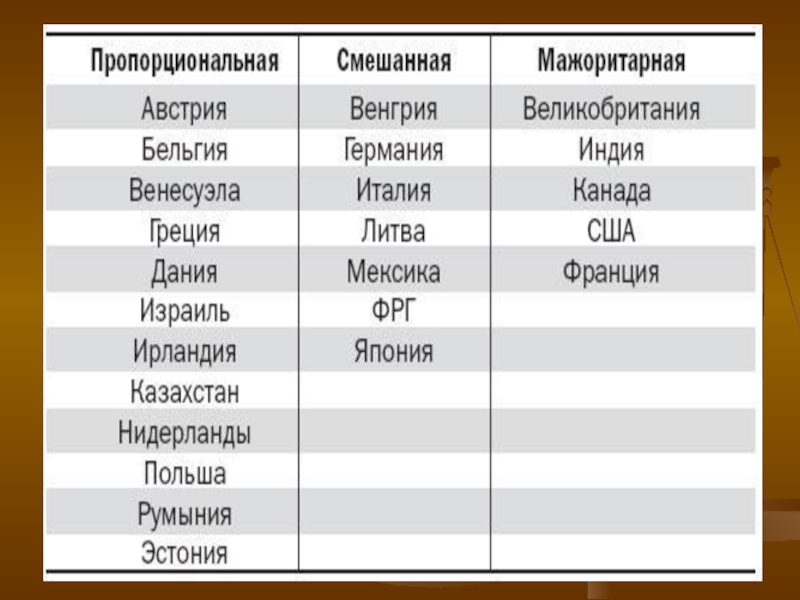
Мажоритарной
Пропорциональной (по партийным спискам)
Иногда законодательство предусматривает сочетание обеих указанных систем

по пропорциональной — 25%; неодинаковы доли в Азербайджане и Венгрии,

где по мажоритарной системе замещаются 2/3 мест в парламенте, а по пропорциональной - 1/3

победившим на выборах считается кандидат, набравший определенное большинство голосов избирателей.

большинства,
квалифицированного большинства.

кандидатов), который набрал голосов больше, чем каждый из его противников

в отдельности, даже если он набрал меньше половины.
Чаще всего применяется в одномандатных округах. Победителем объявляется кандидат, ставший первым по количеству поданных за него голосов, даже если это число существенно ниже 50% проголосовавших. Отсюда и второе название этой системы:
“первый, который считается избранным”

между ними следующим образом:
А-11%;
Б-23%;
В-34%;
Г-32%.
Победившим на

выборах будет признан кандидат В,
набравший 34% голосов избирателей, несмотря на то, что
фактически против него проголосовало 66% избирателей.
Таким образом, голоса 2/3 избирателей остаются
неучтенными, «выброшенными», а депутат в выборном
органе представляет лишь 1/3 избирателей своего округа.

в пяти избирательных округах с равной численностью избирателей в 30 тыc. Борьбу за мандаты вели кандидаты партий А и Б и голоса избирателей распределились между ними следующим образом:
I II III IV V
А 17тыс. 18 16 17 5
Б 13 12 14 13 25

В данном примере партия А получит 4 мандата при общем числе избирателей, проголосовавших за ее кандидатов 73 тыс., а партия Б получит 1 мандат, в то время как за ее кандидатов проголосовало 77 тыс. избирателей. Значит, правящей будет партия, пользующаяся поддержкой меньшинства избирателей.

за кандидата голосов (50% +1).
При такой системе обычно устанавливается

нижний порог участия избирателей в голосовании.
При данной системе также бывает второй тур в его двух вариантах:
на повторное голосование выносятся либо две кандидатуры, набравшие наибольшее количество голосов и проводится так называемая перебаллотировка;
либо все кандидатуры, получившие установленный законом процент голосов.

В обоих случаях избранным считается кандидат, который получит относительное большинство голосов по сравнению с другими.

место – кандидат партии Б (левые силы)
3 место – кандидат

партии В (левые силы)

Б слагает с себя полномочия в пользу В

округе
избиратель голосует только за одного кандидата, а не за список
кандидатов

(Япония).
При этом избранными считаются кандидаты, собравшие больше
голосов, чем другие, т.е. действует принцип мажоритарной
системы относительного большинства.

не обязан отдавать все свои голоса представителям одной
партии, он может

отдать предпочтение двум, трем и более партиям,
участвующим в выборах, т.е. проголосовать за кандидатов из разных партийных списков, ориентируясь не на партийную принадлежность, а на личные качества того или иного кандидата.

округе имеет столько голосов, сколько следует избрать кандидатов (2,3,4) и
распределяет

свои голоса между кандидатами как угодно: может
отдать нескольким кандидатам по одному голосу, либо одному
все голоса. Ныне она применяется при выборах органов местного самоуправления в некоторых землях Германии, в частности в Баварии,

голосование ведется по
партийным спискам. Каждая партия, участвующая в
выборах, получает количество

депутатских мест,
пропорциональное числу полученных ею голосов
избирателей. Эта система строится не на принципе
большинства, а на принципе пропорциональности
между полученными голосами и завоёванными
мандатами.

на основе избирательной квоты, которая вычисляется путем деления общего числа

голосов избирателей, поданных в округе, на число мандатов, подлежащих распределению.
Таким образом, определяется минимальное число голосов избирателей, которое необходимо набрать партии, чтобы получить один мандат (т.е. удельный вес мандата).

5 партий, и голоса избирателей между ними распределились следующим образом:

А-20.000;
Б-16.000;
В-34.000;
Г-43.000;
Д-37.000.

Таким образом, в голосовании приняли участие 150.000 избирателей.
Определяем избирательную квоту: 150.000:6=25.000.
В соответствии с полученной квотой распределяем мандаты между партиями. Для этого число голосов избирателей, полученных каждой партией, делим на избирательную квоту:

А 20.000 : 25.000 = 0 ( 20.000 в остатке )
Б 16.000 : 25.000 = 0 ( 16.000 в остатке )
В 34.000 : 25.000 = 1 ( 9.000 в остатке )
Г 43.000 : 25.000 = 1 ( 18.000 в остатке )
Д 37.000 : 25.000 = 1 ( 12.000 в остатке )

Из 6 мандатов сразу распределить удалось лишь 3 из 6 мандатов.

например, в Германии и Италии в многомандатных округах

Метод наибольшей средней

Используется в Австрии, Бельгии, Нидерландах

голосов избирателей.
В рассматриваемом примере по 1 мандату получат партии

А, Г и Б.

Окончательные результаты будут следующие:
А-1; Б-1; В-1; Г-2; Д-1.

А 20.000 : 25.000 = 0 ( 20.000 в остатке )
Б 16.000 : 25.000 = 0 ( 16.000 в остатке )
В 34.000 : 25.000 = 1 ( 9.000 в остатке )
Г 43.000 : 25.000 = 1 ( 18.000 в остатке )
Д 37.000 : 25.000 = 1 ( 12.000 в остатке )

Чтобы вычислить среднюю каждого
списка, необходимо число голосов избирателей, поданных за

партию, разделить на число полученных ею мандатов плюс 1.
В нашем примере это будет выглядеть так:
А 20.000 : 1 ( 0 мандатов + 1) = 20.000
Б 16.000 : 1 ( 0 мандатов + 1) = 16.000
В 34.000 : 2 ( 1 мандат + 1) = 17.000
Г 43.000 : 2 ( 1 мандат + 1) = 21.500
Д 37.000 : 2 ( 1 мандат + 1) = 18.500
По одному мандату получат партии Г, А и Д, имеющие наибольшую среднюю.

Окончательные результаты будут иными, чем при использовании правила
Наибольшего остатка:
А-1; Б-0; В-1; Г-2; Д-2.

квоте наибольшей средней
А-1; Б-0; В-1; Г-2; Д-2.



А - 20.000;

Б - 16.000;
В - 34.000;
Г - 43.000;
Д - 37.000.

ряд натуральных чисел (1,2,3,4…).
Частные от деления располагаются в убывающем порядке:

43.000, 37.000, 34.000, 21.500, 20.000, 18.500, 17.000, 16.000…
Избирательной квотой будет число, порядковый номер которого соответствует числу мандатов распределяемых в округе (в нашем примере – 6).
Таким образом, избирательным частным будет 18.500.
Разделив голоса на избирательную квоту, получаем такое распределение мандатов:
А-1, Б-0, В-1, Г-2, Д-2.

А 20.000 : 1 ( 0 мандатов + 1) = 20.000
Б 16.000 : 1 ( 0 мандатов + 1) = 16.000
В 34.000 : 2 ( 1 мандат + 1) = 17.000
Г 43.000 : 2 ( 1 мандат + 1) = 21.500
Д 37.000 : 2 ( 1 мандат + 1) = 18.500

партиями окончательная картина выборов будет различной в зависимости от применяемого

способа распределения мандатов.

мандатов, как правило, не возникают.
Кандидаты в списке располагаются не

в алфавитном порядке и не произвольно, а в
зависимости от «веса» кандидата, его положения в партии. Голосуя за список в целом,
избиратели не высказывают отношение к отдельным кандидатам. Выигранные списком
мандаты отдаются кандидатам в соответствии с очередностью их расположения в
списке.

в целом,
избиратель указывает кандидата, которому отдает
предпочтение. Соответственно, мандат получит

кандидат, имеющий наибольшее число
знаков предпочтения.

не просто за список, а проставляет кандидатам в бюллетене
преференции

1, 2, 3..., указывая, тем самым, в какой последовательности избрание
кандидатов для него наиболее желательно. На основе выраженных преференций
определяется индивидуальная цифра каждого кандидата, и в соответствии с
индивидуальными цифрами составляется таблица кандидатов каждого списка. При
равенстве индивидуальных цифр учитывается очередность кандидата в избирательном
списке. По каждому списку, получившему мандат, избранным считается кандидат,
имеющий наибольшую индивидуальную цифру.

традиционной данная система являлась для формирования Государственной Думы, когда 225

мандатов определялись по округам (мажоритарное начало), а оставшиеся 225 мандатов формировались по партийным спискам.

выборах депутатов Государственной Думы Федерального Собрания Российской Федерации“ (с изм.

от 2 мая 2012 г. N 41-ФЗ)

не являющихся членами политических партий. Указанные лица могут составлять не

более 50 процентов от числа кандидатов, включенных в федеральный список кандидатов. Политическая партия не вправе включать в федеральный список кандидатов лиц, являющихся членами иных политических партий.

на региональные группы кандидатов, соответствующие субъекту Российской Федерации, группе субъектов

Российской Федерации, части территории субъекта Российской Федерации. 9.1. Политическая партия вправе определить региональную группу кандидатов, к которой будут отнесены поданные за федеральный список кандидатов голоса избирателей, проживающих за пределами территории Российской Федерации. 10. Число избирателей, зарегистрированных на территории группы субъектов Российской Федерации, которой соответствует региональная группа кандидатов, не может превышать 3 миллиона. Число избирателей, зарегистрированных на части территории субъекта Российской Федерации, которой соответствует региональная группа кандидатов, не может быть менее 650 тысяч. 11. Региональная группа кандидатов может соответствовать части территории субъекта Российской Федерации при условии, что численность зарегистрированных на всей территории данного субъекта Российской Федерации избирателей превышает 1,3 миллиона.