Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тепловое излучение
Содержание
- 1. Тепловое излучение
- 2. Излучение телами электромагнитных волн – свечение тел
- 3. Излучение неравновесное и равновесное Окружим излучающее тело
- 4. Излучение неравновесное и равновесное Хемилюминесценция – свечение
- 5. Излучение неравновесное и равновесное Тепловое излучениеЕсли равновесие
- 6. Энергетическая светимость RВведем величину, которая может быть
- 7. Закон КирхгофаОпределенияКоличество энергии, испущенное единицей поверхности за
- 8. Закон КирхгофаОпределенияЕсли характеризовать излучение не частотой, а
- 9. Закон КирхгофаОпределенияДля произвольного участка спектра испускательнаяспособность в
- 10. Закон КирхгофаОпределенияОтношение лучистой энергиипоглощенной некоторой площадкой к
- 11. Закон КирхгофаОпределенияТело, которое полностью поглощает всю упавшую
- 12. Закон КирхгофаДля абсолютно черного телапоэтомуТаким образом, универсальная функция Кирхгофаесть испускательная способность абсолютно черного тела!
- 13. Смысл функциизаключается в том, что она представляет
- 14. В экспериментальных исследованиях удобнейкоторая связана с частотной
- 15. Закон Стефана - БольцманаВ 1879 году Стефан
- 16. Закон Стефана - БольцманаВ 1879 году Стефан
- 17. Закон Стефана - БольцманаЭнергетическая светимость пропорциональна четвёртоё степени температурыПостоянная Стефана – Больцмана равна
- 18. Закон смещения ВинаВ 1893 году Вин установил,
- 19. Закон смещения ВинаВ 1893 году Вин установил,
- 20. Закон смещения Вина
- 21. Закон смещения ВинаВсе эти кривые – результат экспериментального наблюдения
- 22. Формула ПланкаТеоретически зависимость получил Макс Планк в
- 23. Формула ПланкаПредложенная Планком зависимость имеет вид: в которой постоянная Больцмана равна
- 24. Формула ПланкаПредложенная Планком зависимость имеет вид: в которой постоянная Больцмана равна
- 25. Формула ПланкаПереход к частотной спектральной плотности осуществим по формулеоткуда
- 26. Вывод закона Стефана – Больцмана из формулы
- 27. Вывод закона Стефана – Больцмана из формулы
- 28. Вывод закона Стефана – Больцмана из формулы Планкаоткуда
- 29. Вывод закона Стефана – Больцмана из формулы Планкаоткуда
- 30. Вывод закона Стефана – Больцмана из формулы ПланкаследовательноИнтеграл можно вычислитьоткуда
- 31. Получение закона смещения Винаиз формулы ПланкаследовательноИнтеграл можно
- 32. Пример 1.меняется медленно.Солнце вполне можно считать чёрным
- 33. Пример 1.В соответствии с законом смещения Винагде
- 34. Пример 2.Температура поверхности СолнцаСчитая, что поглощательная способность
- 35. Пример 2.С единицы поверхности Солнца ежесекундно уходит
- 36. Пример 2.Энергия равномерно распределена по сфере с
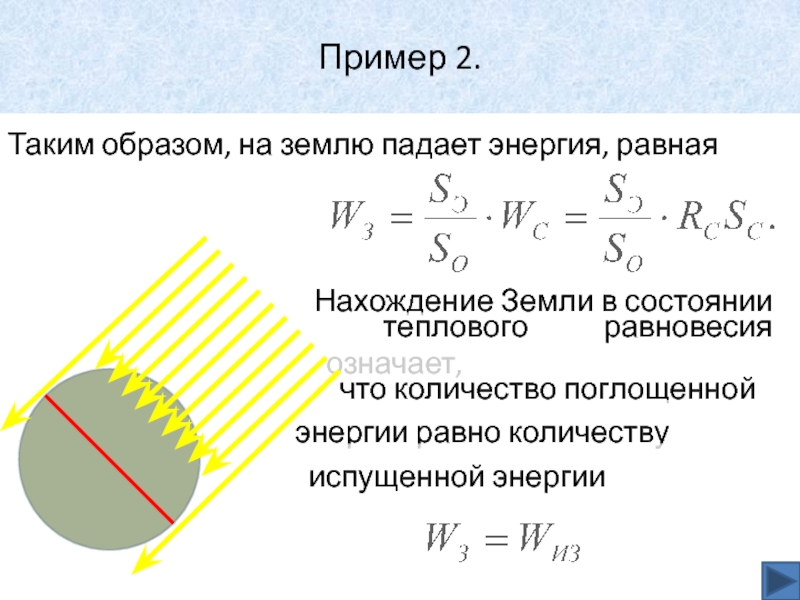
- 37. Пример 2.Таким образом, на землю падает энергия,
- 38. Пример 2.Состояние теплового равновесия: Сколько энергии приходит, столько и уходит(по всем направлениям).Отсюда:
- 39. Пример 2.Однако энергия, испущенная Землёй, тоже может быть выражена через её испускательную способностьОкончательно получаем:
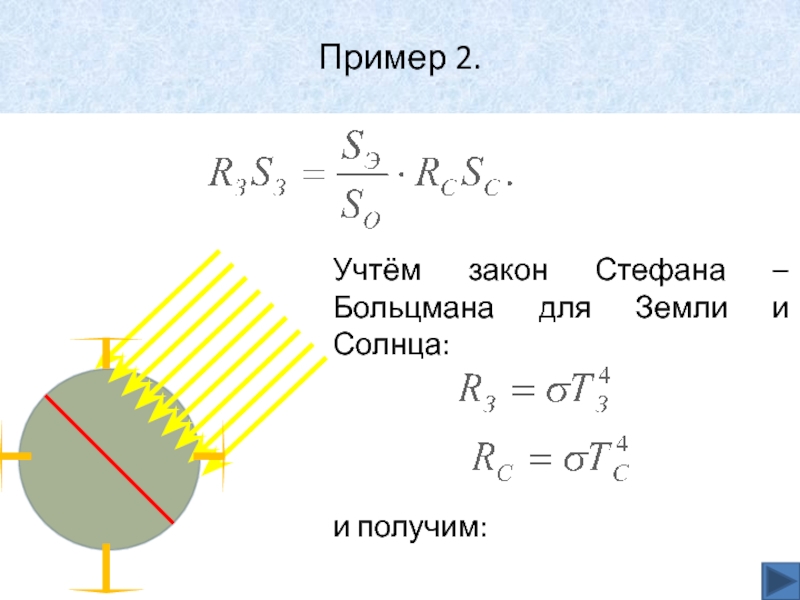
- 40. Пример 2.Учтём закон Стефана – Больцмана для Земли и Солнца:и получим:
- 41. Пример 2.В этом выражении площади равны соответственно:–
- 42. Пример 2.Подставляя, получаем:Сократим всё, что сокращается и получим:
- 43. Пример 2.Извлекая корень четвертой степени, будем иметь:Подставим табличные значенияи подсчитаем самостоятельно.
- 44. Ключевые понятия и выводы Тепловое излучение.Абсолютно черное
- 45. Ключевые формулы
- 46. Ключевые формулы
- 47. ☺
- 48. Скачать презентанцию
Излучение телами электромагнитных волн – свечение тел Испускание электромагнитных волн за счет внутренней энергии телаТепловое излучениеЛюминесценция хемилюминесценция электролюминесценция катодолюминесценция …Тепловое излучение – наиболее распространенный вид излучения, который имеет место при любой
Слайды и текст этой презентации
Слайд 2Излучение телами электромагнитных волн – свечение тел
Испускание электромагнитных волн
за счет внутренней энергии тела
излучение – наиболее распространенный вид излучения, который имеет место при любой температуре
Слайд 3Излучение неравновесное и равновесное
Окружим излучающее тело оболочкой с идеально
отражающей поверхностью, из которой удалим воздух .
Отраженное оболочкой излучение, упав
на тело , частично или полностью поглотится им.Если распределение энергии между телом и излучением остается неизменным для каждой длины волны,
состояние системы тело – излучение будет равновесным
Слайд 4Излучение неравновесное и равновесное
Хемилюминесценция – свечение тел в результате
протекания химической реакции
По мере излучения тело расходует запас химических веществ.
Поглощение
отраженного стенкой излучения ведет к нагреву и ускорению химической реакции.Люминесценция – неравновесный процесс
Слайд 5Излучение неравновесное и равновесное
Тепловое излучение
Если равновесие нарушено, и тело
излучает больше, чем поглощает, его внутренняя энергия уменьшается – тело
остывает и количество излучённой энергии уменьшаетсяЕсли тело поглощает больше, чем излучает – его внутренняя энергия увеличивается, а тело нагревается
Тепловое излучение – равновесный процесс
Слайд 6
Энергетическая светимость R
Введем величину, которая может быть найдена как отношение
всей испущенной нагретым телом за время t энергии W к
площади поверхности тела S и к этому времени.
Слайд 7Закон Кирхгофа
Определения
Количество энергии, испущенное единицей поверхности за единицу времени (поток
энергии) в пределах полусферы называют энергетической светимостью и обозначают R.
Поток
энергии, испускаемый в узком интервале частот пропорционален ширине этого интервала
Коэффициент пропорциональности
называют
испускательной способностью тела
Слайд 8Закон Кирхгофа
Определения
Если характеризовать излучение не частотой, а длиной
волны, то выражение
для испускательной способности
получим, используя связь частоты и длины волны
Отсюда,
после дифференцирования, получаемгде знак «–» указывает, что при возрастании длины волны частота убывает.
Слайд 9Закон Кирхгофа
Определения
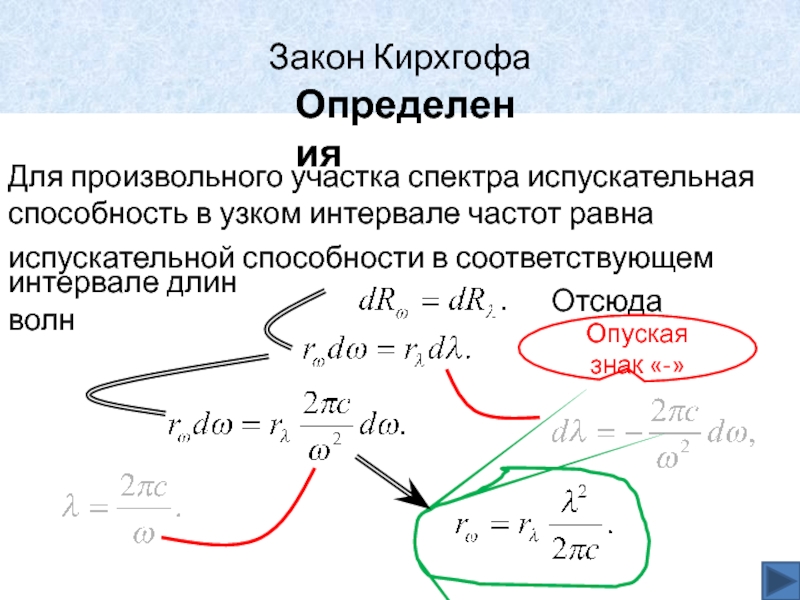
Для произвольного участка спектра испускательная
способность в узком интервале частот
равна
испускательной способности в соответствующем
интервале длин волн
Отсюда
Опуская знак «-»
Слайд 10Закон Кирхгофа
Определения
Отношение лучистой энергии
поглощенной некоторой площадкой к энергии
упавшей на
эту площадку, называют
поглощательной способностью
из интервала
По определению
Слайд 11Закон Кирхгофа
Определения
Тело, которое полностью поглощает всю упавшую на него
энергию, называется
абсолютно черным телом.
Для абсолютно черного тела поглощательная способность
Слайд 12Закон Кирхгофа
Для абсолютно черного тела
поэтому
Таким образом, универсальная функция Кирхгофа
есть испускательная
способность абсолютно черного тела
!
Слайд 13
Смысл функции
заключается в том, что она представляет собой
спектральную плотность излучения,
то есть показывает,
сколько энергии излучает абсолютно черное тело в
единичном интервале
частот или длин волн.Закон Кирхгофа
Слайд 14
В экспериментальных исследованиях удобней
которая связана с частотной функцией соотношением
где частота
и длина волны также связаны:
пользоваться функцией длины волны
Закон Кирхгофа
Слайд 15Закон Стефана - Больцмана
В 1879 году Стефан предположил, что
В 1884
Больцман,
исходя из термодинамических соображений,
для абсолютно черных тел получил
теоретически выражение – постоянная Стефана – Больцмана.
Слайд 16Закон Стефана - Больцмана
В 1879 году Стефан установил, что
В 1884
Больцман,
исходя из термодинамических соображений
получил теоретически выражение
– постоянная
Стефана – Больцмана.
Слайд 17Закон Стефана - Больцмана
Энергетическая светимость пропорциональна
четвёртоё степени температуры
Постоянная Стефана
– Больцмана равна
Слайд 18Закон смещения Вина
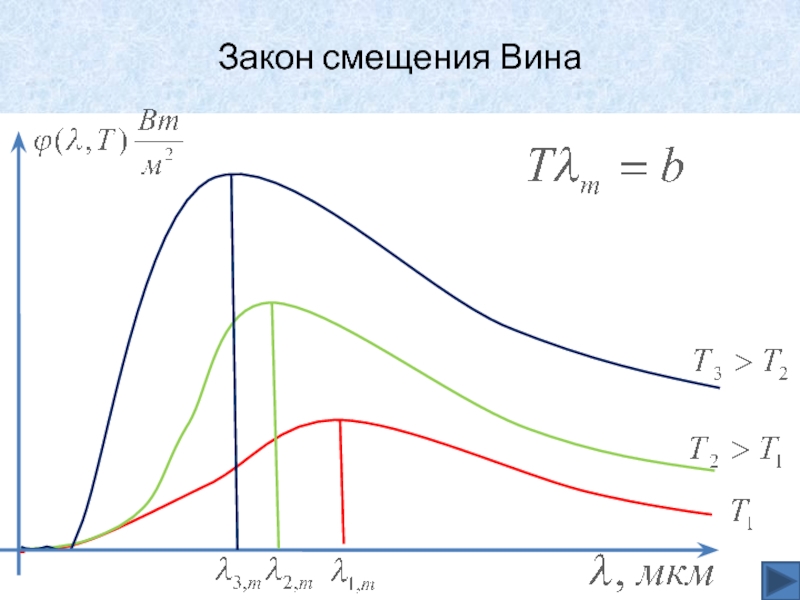
В 1893 году Вин установил, что
длина волны,
соответствующая максимуму функции спектрального распределения связанна с температурой соотношением
– постоянная
в законе смещения Вина.
Слайд 19Закон смещения Вина
В 1893 году Вин установил, что
длина волны,
соответствующая максимуму функции спектрального распределения связанна с температурой соотношением
– постоянная
в законе смещения Вина.
Слайд 22Формула Планка
Теоретически зависимость
получил Макс Планк в 1900, сделав чуждое
классической
физике предположение, что электромагнитное излучение
испускается порциями энергии, величина которых
равнагде
– постоянная Планка, читается «аш с чертой».
Слайд 23Формула Планка
Предложенная Планком зависимость имеет вид:
в которой постоянная Больцмана
равна
Слайд 24Формула Планка
Предложенная Планком зависимость имеет вид:
в которой постоянная Больцмана
равна
Слайд 26Вывод закона Стефана – Больцмана
из формулы Планка
Для получения закона
Стефана – Больцмана
в котором сделаем замену переменных
Формула Планка
воспользуемся частотной спектральной
плотностью Энергетическая светимость определяется выражением
Слайд 27Вывод закона Стефана – Больцмана
из формулы Планка
Для получения закона
Стефана – Больцмана
в котором сделаем замену переменных
Воспользуемся частотной спектральной плотностью
Энергетическая светимость определяется выражением
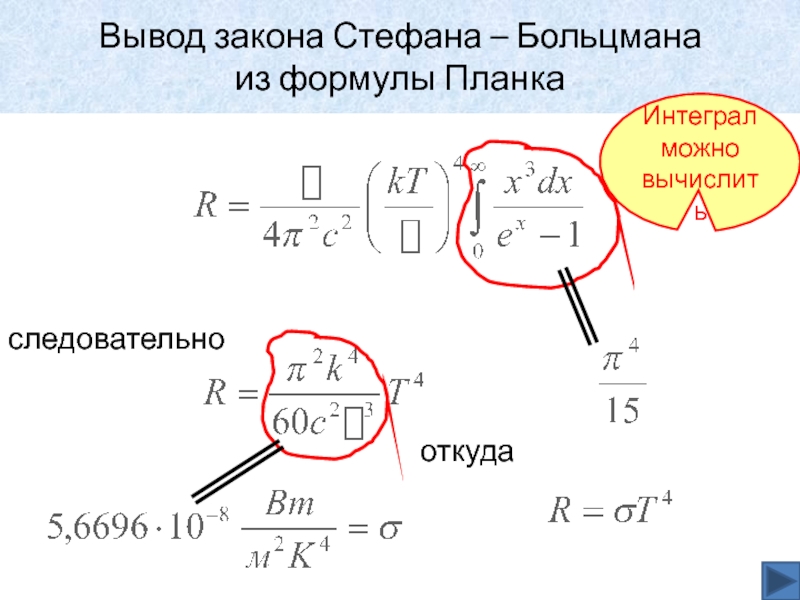
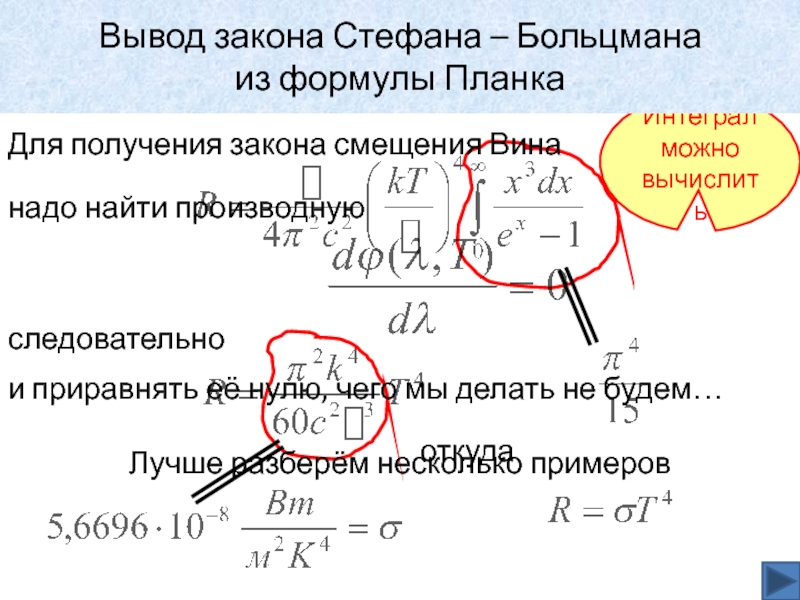
Слайд 30Вывод закона Стефана – Больцмана
из формулы Планка
следовательно
Интеграл можно вычислить
откуда
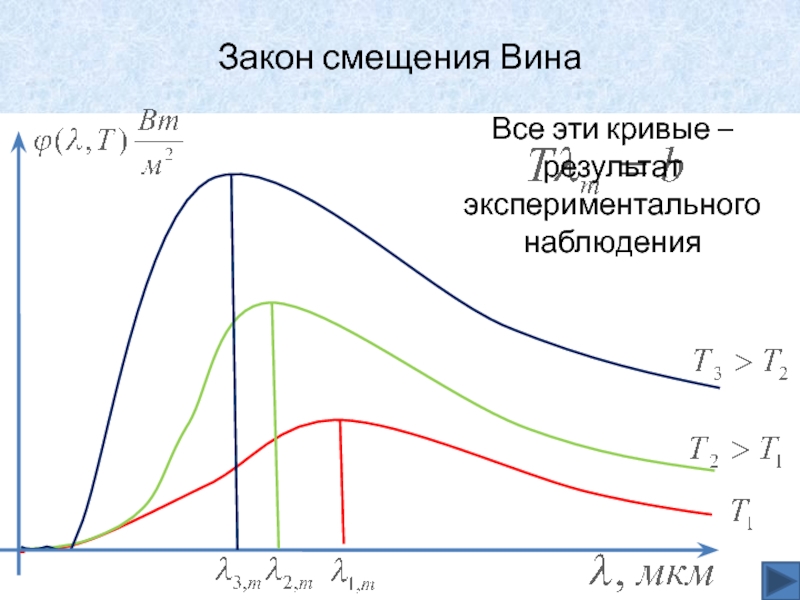
Слайд 31Получение закона смещения Вина
из формулы Планка
следовательно
Интеграл можно вычислить
откуда
Вывод закона Стефана
– Больцмана
из формулы Планка
Для получения закона смещения Вина
надо
найти производнуюи приравнять её нулю, чего мы делать не будем…
Лучше разберём несколько примеров
Слайд 32Пример 1.
меняется медленно.
Солнце вполне можно считать чёрным телом, так как
падающий на него свет проникает в глубинные слои,
почти не
испытывая отражения. Это объясняется тем, что плотность слоёв (и их показатель преломления)
Область максимального излучения Солнца
приходится примерно на длину волны
Оценим температуру поверхности Солнца
Слайд 33Пример 1.
В соответствии с законом смещения Вина
где постоянная b равна
Отсюда
получаем:
Подставляя численные значения, имеем:
Более точные расчеты дадут
Слайд 34Пример 2.
Температура поверхности Солнца
Считая, что поглощательная способность Солнца и
Земли равна
единице и что Земля находится в состоянии
теплового равновесия, оценить её
температуру.Будем считать, что Солнце
испускает лучистую энергию
равномерно по всем
направлениям.
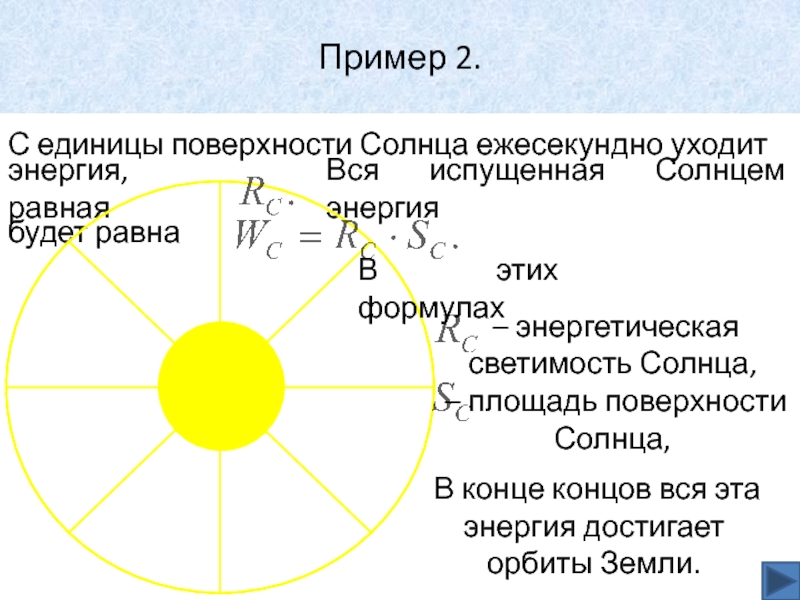
Слайд 35Пример 2.
С единицы поверхности Солнца ежесекундно уходит
энергия, равная
Вся
испущенная Солнцем энергия
будет равна
В этих формулах
– энергетическая светимость Солнца,
– площадь поверхности Солнца,
В конце концов вся эта энергия достигает орбиты Земли.
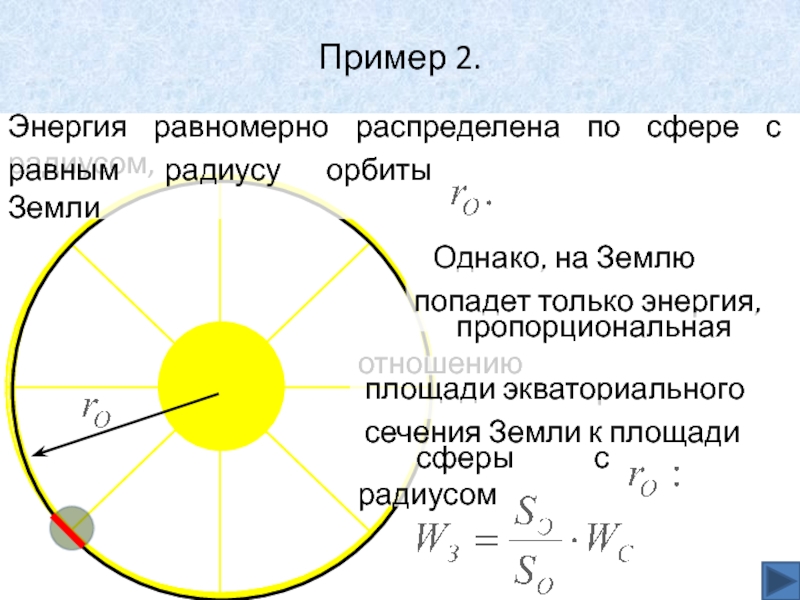
Слайд 36Пример 2.
Энергия равномерно распределена по сфере с радиусом,
равным радиусу орбиты
Земли
Однако, на Землю
попадет только энергия,
пропорциональная отношению
площади экваториального
сечения Земли к площади сферы с радиусом
Слайд 37Пример 2.
Таким образом, на землю падает энергия, равная
Нахождение Земли в
состоянии
теплового равновесия означает,
что количество поглощенной
энергии равно количеству
испущенной
энергии
Слайд 38Пример 2.
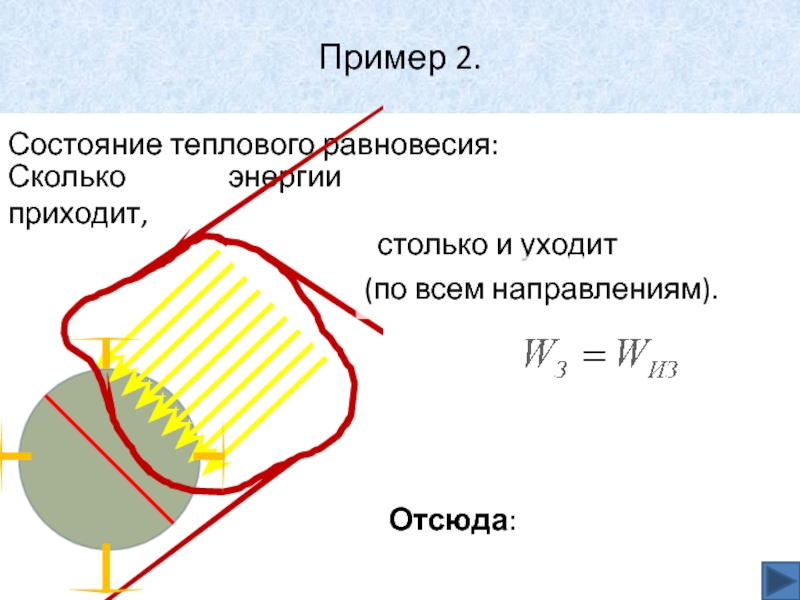
Состояние теплового равновесия:
Сколько энергии приходит,
столько и уходит
(по
всем направлениям).
Отсюда:
Слайд 39Пример 2.
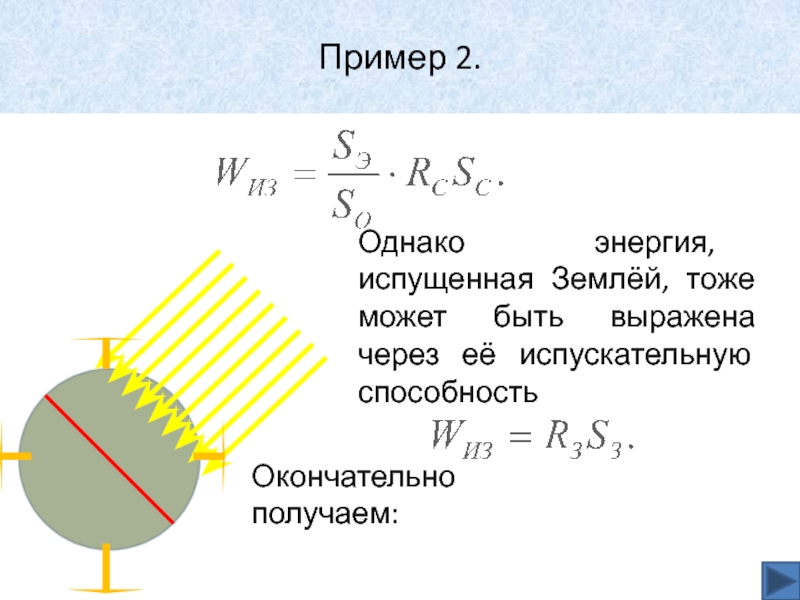
Однако энергия, испущенная Землёй, тоже может быть выражена через
её испускательную способность
Окончательно получаем:
Слайд 41Пример 2.
В этом выражении площади равны соответственно:
– площадь поверхности Земли,
–
площадь экваториального сечения Земли,
– площадь сферы, «натянутой» на орбиту Земли,
–
площадь поверхности Солнца.
Слайд 43Пример 2.
Извлекая корень четвертой степени, будем иметь:
Подставим табличные значения
и подсчитаем
самостоятельно.
Слайд 44Ключевые понятия и выводы
Тепловое излучение.
Абсолютно черное тело.
Энергетическая светимость.
Связь энергетической светимости
с температурой – закон Стефана-Больцмана.
Зависимость от температуры максимума функции спектральной
плотности излучения – закон смещения Вина.Зависимость функции спектральной плотности излучения от температуры – формула Планка.
