Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы квантовой механики
Содержание
- 1. Элементы квантовой механики
- 2. Луи Де Бройль (1892-1987)1924 г.Выдвинул гипотезу о
- 3. Иллюстрация идеи де Бройля возникновения стоячих волн на
- 4. х «В оптике, – писал де Бройль, –
- 5. х Если фотон обладает энергией E = hv
- 6. х Волновой вектор монохроматической волны, связанной со свободно
- 7. х Поскольку кинетическая энергия сравнительно медленно движущейся частицы
- 8. х При взаимодействии частицы с
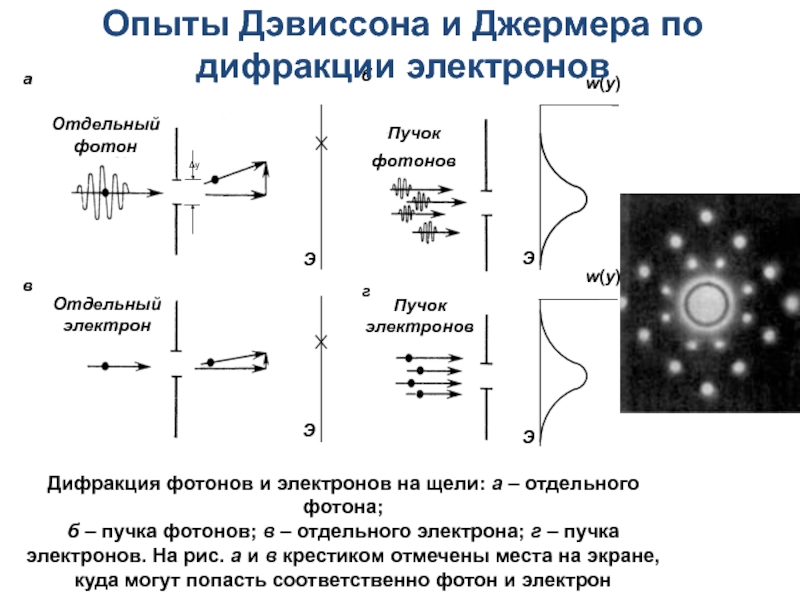
- 9. Опыты Дэвиссона и Джермера по дифракции электронов
- 10. х Кристаллы обладают высокой степенью упорядоченности. Атомы в
- 11. х Если ускорять электроны электрическим полем с
- 12. х При напряжениях U порядка
- 13. Дифракция электронов на кристаллической решеткеЧастицыВолныNСоотношениеБрэгга-Вульфаd – межплоскостное расстояниеРазность хода:Δ=2dsinθ
- 14. Позднее была обнаружена дифракция протонов, нейтронов, и атомов водорода.
- 15. Картина дифракции электронов на слюде
- 16. Картина дифракции нейтронов на кварце
- 17. Корпускулярно-волновой дуализм электронаВыводы:Принципиально невозможно определить координату точки
- 18. Слайд 18
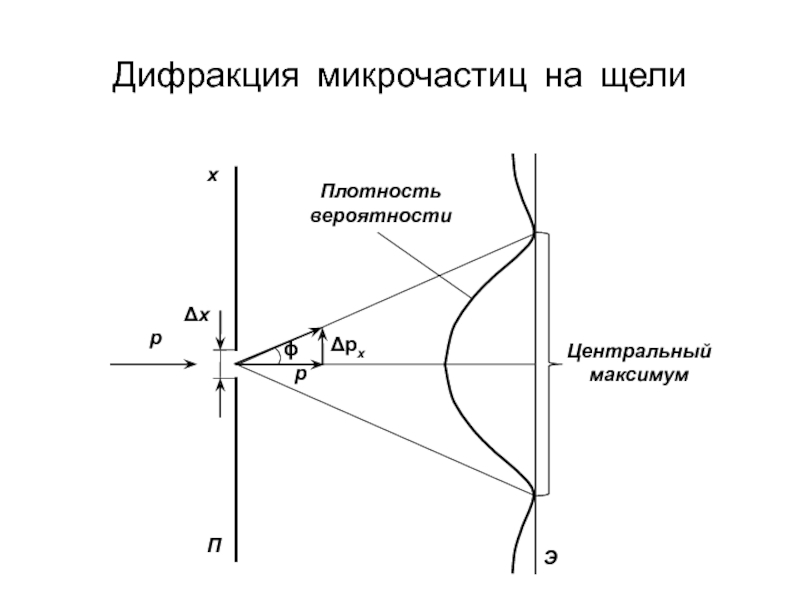
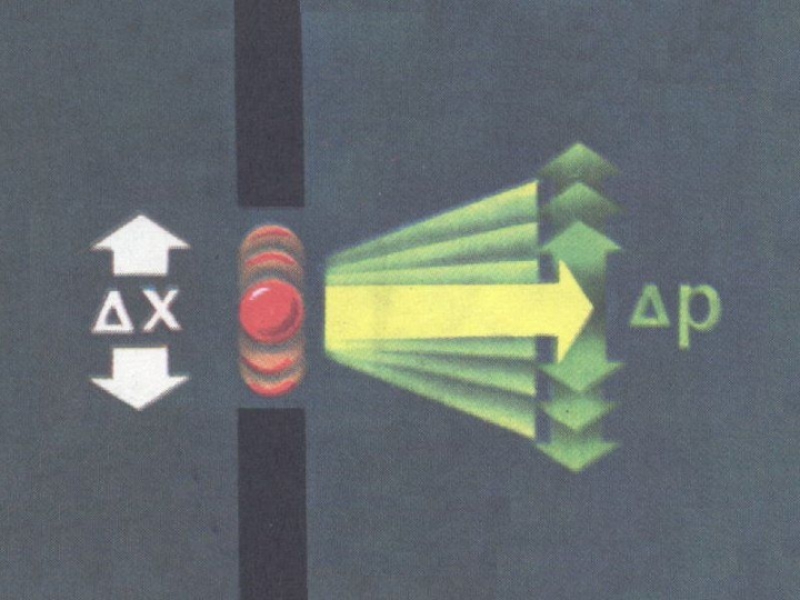
- 19. Дифракция микрочастиц на щели
- 20. Вернер Карл Гейзенберг(1901-1976)1927 г.Сформулировал принцип неопределённостиНобелевская премия 1932 г.ГдеΔX – неопределённость координатыΔP – неопределённость импульса
- 21. Слайд 21
- 22. Утверждение о том,
- 23. х3.Понятие о волновой функции Экспериментальное подтверждение идеи
- 24. х Необходимость вероятностного подхода к описанию микрочастиц, является
- 25. х Чтобы устранить эти трудности немецкий физик М.
- 26. х Таким образом, описание микрообъекта с помощью волновой
- 27. хИтак, в квантовой механике состояние частицы описывается
- 28. х Величина (квадрат модуля Ψ –
- 29. Вероятность найти частицу в момент
- 30. хгде данный интеграл вычисляется по всему бесконечному
- 31. Ну и что ? Какая польза нам от знания волновой функции?
- 32. Вместо непрерывных траекторий волновая модель
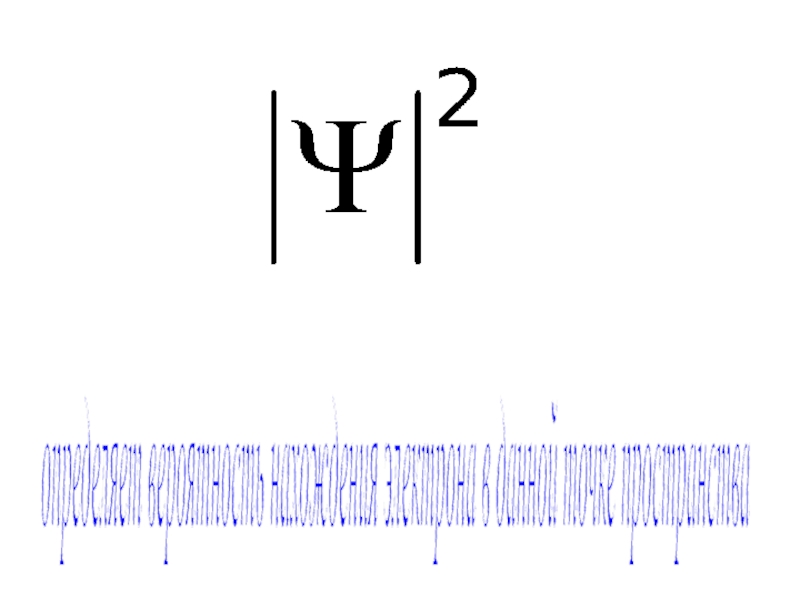
- 33. определяет вероятность нахождения электрона в данной точке пространства
- 34. Квадрат
- 35. Чтобы волновая функция являлась объективной характеристикой состояния
- 36. х Волновая функция удовлетворяет принципу суперпозиции: если система
- 37. х Сложение волновых функций (амплитуд вероятностей определяемых квадратами
- 38. х Волновая функция Ψ является основной характеристикой состояния
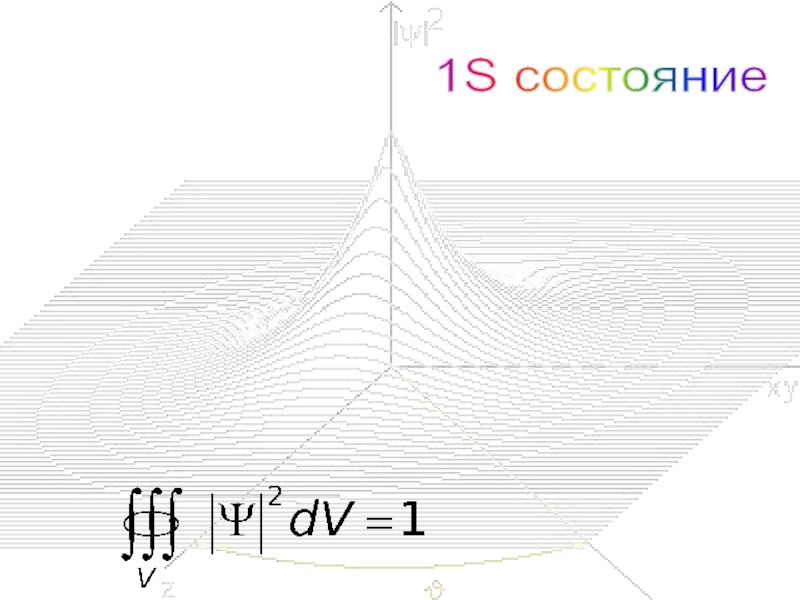
- 39. 1S состояние
- 40. х4. Уравнение Шредингера Толкование волн де Бройля
- 41. х Основное уравнение должно быть уравнением относительно
- 42. хШредингер Эрвин (1887 – 1961) – австрийский
- 43. х Уравнение Шредингера не выводится, а постулируется. Правильность
- 44. х Уравнение Шредингера в
- 45. х Если силовое поле, в котором движется частица
- 46. Уравнение Шредингера для стационарных состояний
- 47. х Уравнение Шредингера для стационарных состояний можно переписать
- 48. х В квантовой механике и другим динамическим переменным
- 49. Эрвин Шрёдингер (1887-1961) Любое движениемикрочастиц можноуподобить движениюособых волн
- 50. Для стационарных Состояний при движении по одной оси х
- 51. Атом водорода с точки зрения квантовой теорииИсходные
- 52. Слайд 52
- 53. Распределение вероятности обнаружения электрона в атоме водорода
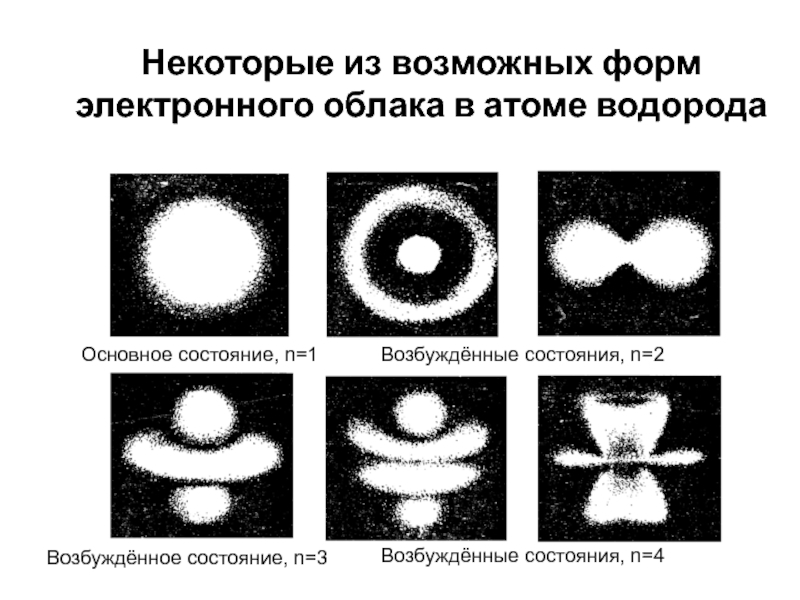
- 54. Возбуждённое состояние, n=3Некоторые из возможных форм электронного
- 55. Скачать презентанцию
Луи Де Бройль (1892-1987)1924 г.Выдвинул гипотезу о корпускулярно-волновом дуализме электронов, атомов и других микрочастицНобелевская премия 1929 г.1. Гипотеза де Бройля
Слайды и текст этой презентации
Слайд 1Тема. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
1. Физический смысл волн де Бройля
2.
Принцип неопределенности
Слайд 2Луи Де Бройль
(1892-1987)
1924 г.
Выдвинул гипотезу о корпускулярно-волновом дуализме электронов, атомов
и других микрочастиц
Нобелевская премия 1929 г.
1. Гипотеза де Бройля
Слайд 3Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите в
боровской модели атома водорода для случая n = 4
Слайд 4х
«В оптике, – писал де Бройль, – в течение столетия
слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не
делалась ли в теории вещества обратная ошибка?»Допуская, что частицы вещества наряду с корпускулярными свойствами имеют также и волновые, де Бройль перенес на случай частиц вещества те же правила перехода от одной картины к другой, какие справедливы в случае света.
Слайд 5х
Если фотон обладает энергией E = hv и импульсом p
= h/λ, то и частица (например, электрон), движущаяся с некоторой
скоростью, обладает волновыми свойствами, т.е. движение частицы можно рассматривать как движение волны.p = h/λ
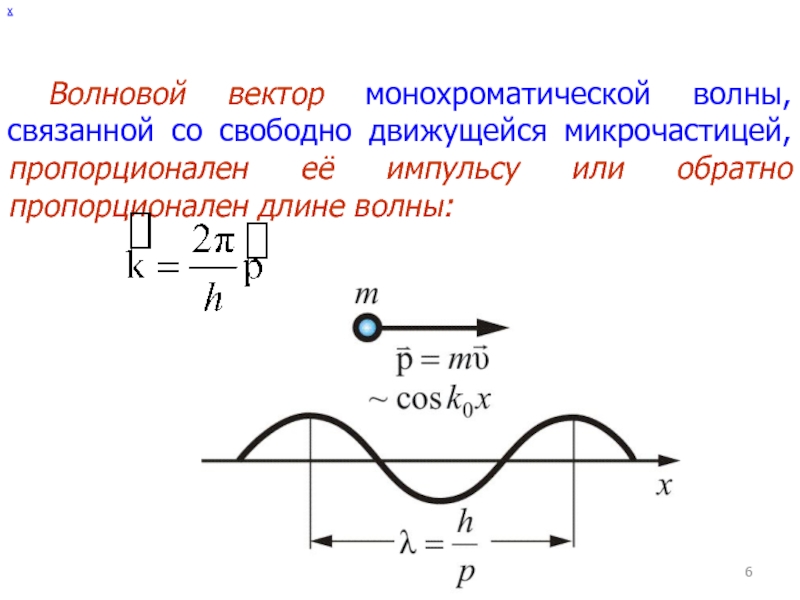
Слайд 6х
Волновой вектор монохроматической волны, связанной со свободно движущейся микрочастицей, пропорционален
её импульсу или обратно пропорционален длине волны:
Слайд 7х
Поскольку кинетическая энергия сравнительно медленно движущейся частицы
K = mv2/2,
то длину волны можно выразить и через энергию:
(4)
Слайд 8х
При взаимодействии частицы с некоторым объектом -
с кристаллом, молекулой и т.п. – её энергия меняется:
к
ней добавляется потенциальная энергия этого взаимодействия, что приводит к изменению движения частицы. Соответственно, меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений.
Поэтому, основные геометрические закономерности дифракции частиц, ничем не отличаются от закономерностей дифракции любых волн.
Общим условием дифракции волн любой природы является соизмеримость длины падающей волны λ с расстоянием d между рассеивающими центрами: λ ≤ d
Слайд 10х
Кристаллы обладают высокой степенью упорядоченности.
Атомы в них располагаются в
трёхмерно-периодической кристаллической решётке, т.е. образуют пространственную дифракционную решётку для соответствующих
длин волн.Дифракции электронов на монокристаллах никеля
Слайд 11х
Если ускорять электроны электрическим полем с напряжением U, то
они приобретут кинетическую энергию K = eU, (е – заряд
электрона), что после подстановки в равенствочисловых значений даёт
(5)
Дифракции электронов на монокристаллах никеля
Здесь U выражено в В, а λ – в Å (1 Å = 10–10 м).
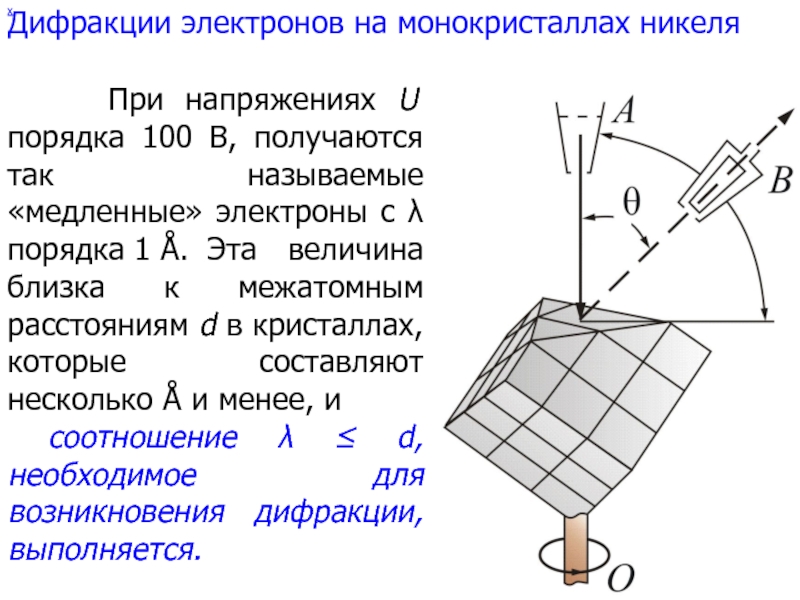
Слайд 12х
При напряжениях U порядка 100 В, получаются
так называемые «медленные» электроны с λ порядка 1 Å. Эта
величина близка к межатомным расстояниям d в кристаллах, которые составляют несколько Å и менее, исоотношение λ ≤ d, необходимое для возникновения дифракции, выполняется.
Дифракции электронов на монокристаллах никеля
Слайд 13
Дифракция электронов на кристаллической решетке
Частицы
Волны
N
Соотношение
Брэгга-Вульфа
d – межплоскостное расстояние
Разность хода:
Δ=2dsinθ
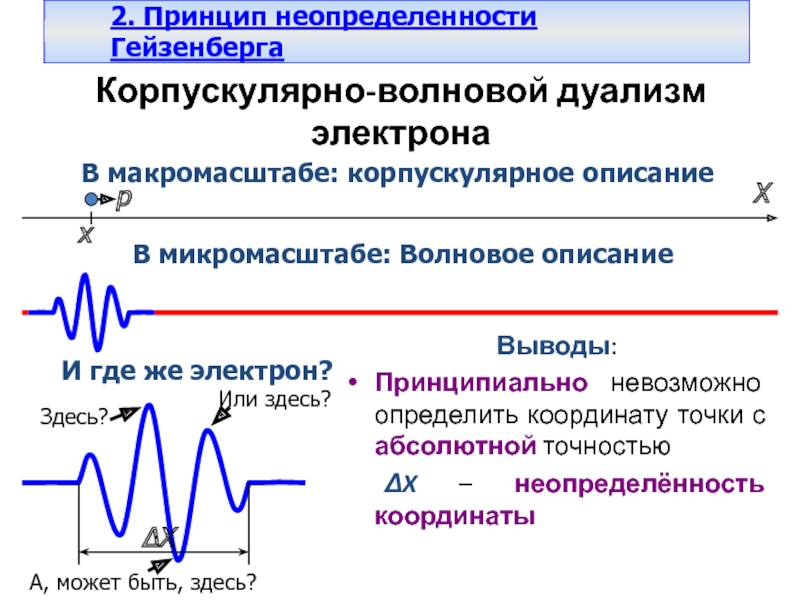
Слайд 17Корпускулярно-волновой дуализм электрона
Выводы:
Принципиально невозможно определить координату точки с абсолютной точностью
ΔX
– неопределённость координаты
X
В макромасштабе: корпускулярное описание
В микромасштабе: Волновое описание
И где
же электрон?Здесь?
Или здесь?
А, может быть, здесь?
2. Принцип неопределенности
Гейзенберга
Слайд 20Вернер Карл Гейзенберг
(1901-1976)
1927 г.
Сформулировал принцип неопределённости
Нобелевская премия 1932 г.
Где
ΔX –
неопределённость координаты
ΔP – неопределённость импульса
Слайд 22 Утверждение о том, что произведение неопределенностей
значений двух сопряженных переменных не может быть по порядку меньше
постоянной Планка, называется принципом неопределенности Гейзенберга.Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей
х
Слайд 23х
3.Понятие о волновой функции
Экспериментальное подтверждение идеи де Бройля об
универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая
соотношением неопределенностей, а также противоречия ряда экспериментов с применяемыми в начале XX века теориями привели к новому этапу развития квантовой физики – созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств. Ее создание и развитие охватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20-х годов XX века и связано, прежде всего, с работами австрийского физика Э. Шредингера, немецкого физика В. Гейзенберга и английского физика П. Дирака.
Слайд 24х
Необходимость вероятностного подхода к описанию микрочастиц, является важнейшей отличительной особенностью
квантовой теории.
Можно ли волны де Бройля истолковывать как волны
вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно, хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.
Слайд 25х
Чтобы устранить эти трудности немецкий физик М. Борн в 1926
г. предположил, что по волновому закону меняется не сама вероятность,
а величина, названная амплитудой вероятности и обозначаемаяΨ(х, y, z, t).
Эту величину называют также волновой функцией (или Ψ – функцией).
Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:
где |Ψ|2=ΨΨ* , где Ψ* – функция комплексно-сопряженная с Ψ.
Слайд 26х
Таким образом, описание микрообъекта с помощью волновой функции имеет статистический,
вероятностный характер:
квадрат модуля волновой функции (квадрат модуля амплитуды волн
де Бройля) определяет вероятность нахождения частицы в момент времени в области с координатами x и dx, y и dy, z и dz. 
Слайд 27х
Итак, в квантовой механике состояние частицы описывается принципиально по-новому –
с помощью волновой функции, которая является основным носителем информации об
их корпускулярных и волновых свойствах.Вероятность нахождения частицы в объеме V равна:
(6)
Слайд 28х
Величина (квадрат модуля Ψ – функции) имеет смысл
плотности вероятности, т.е. определяет вероятность нахождения частицы в единице объема
в окрестности точки, имеющей x, y, z.Таким образом, физический смысл имеет не сама Ψ – функция, а квадрат ее модуля
, которым определяется интенсивность волн де Бройля.
Слайд 29 Вероятность найти частицу в момент времени t в
конечном объеме V, согласно теореме о сложении вероятностей, равна:
х
Т.к.
|Ψ|2dV определяется как вероятность, то необходимо волновую функцию Ψ представить так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве.
Условия нормировки вероятностей:
Слайд 30х
где данный интеграл вычисляется по всему бесконечному пространству, т.е. по
координатам x, y, z от –∞ до ∞.
Таким
образом, условие нормировки говорит об объективном существовании частицы во времени и пространстве. Условия нормировки вероятностей:
Слайд 32Вместо непрерывных
траекторий
волновая модель
предлагает
картину распределения
электронной плотности
по всему пространству.
Слайд 35 Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна
удовлетворять ряду ограничительных условий.
Функция Ψ, характеризующая вероятность
обнаружить действия микрочастицы в элементе объема, должна быть:конечной (вероятность не может быть больше единицы);
однозначной (вероятность не может быть неоднозначной величиной);
непрерывной (вероятность не может меняться скачком).
х
Слайд 36х
Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в
различных состояниях, описываемых волновыми функциями Ψ1, Ψ2, … Ψn, то
она может находиться в состоянии, описываемом линейной комбинацией этих функцийгде Cn (n = 1, 2, 3…) – произвольные, комплексные числа.
Слайд 37х
Сложение волновых функций (амплитуд вероятностей определяемых квадратами модулей волновых функций)
принципиально отличает квантовую теорию от классической статической теории, в которой
для независимых событий справедлива теорема сложения вероятностей.
Слайд 38х
Волновая функция Ψ является основной характеристикой состояния микрообъектов.
Например, среднее
расстояние электрона от ядра вычисляется по формуле
Слайд 40х
4. Уравнение Шредингера
Толкование волн де Бройля и соотношение неопределенностей
Гейзенберга привели к выводу, что уравнением движения в квантовой механике,
описывающей движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц.
Слайд 41х
Основное уравнение должно быть уравнением относительно волновой функции Ψ(х,
y, z, t), т.к. именно величина |Ψ|2, осуществляет вероятность пребывания
частицы в момент времени t в объеме dV, т.е. в области с координатами x и x+dx, y, и y+dy, z и z+dz.Т.к. искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э.Шредингером.
Слайд 42х
Шредингер Эрвин (1887 – 1961) – австрийский физик-теоретик, один из
создателей квантовой механики. Основные работы в области статистической физики, квантовой
теории, квантовой механики, общей теории относительности, биофизики.Разработал теорию движения микрочастиц – волновую механику, построил квантовую теорию возмущений – приближенный метод в квантовой механике. За создание волновой механики удостоен Нобелевской премии.
Слайд 43х
Уравнение Шредингера не выводится, а постулируется.
Правильность этого уравнения подтверждается
согласием с опытом получаемых с его помощью результатов, что в
свою очередь, придает ему характер закона природы.
Слайд 44х
Уравнение Шредингера в общем виде записывается
так:
где
- постоянная Планка, m – масса частицы.
– оператор Лапласа
i – мнимая единица,
U(x, y, z, t) – потенциальная функция частицы в силовом поле, в котором она движется,
Ψ – искомая волновая функция.
Слайд 45х
Если силовое поле, в котором движется частица потенциально, то функция
U не зависит явно от времени и имеет смысл потенциальной
энергии.В этом случае решение уравнения Шредингера распадается на два сомножителя, один из которых зависит только от координаты, а другой – только от времени.
Здесь E – полная энергия частицы, которая в случае стационарного поля остается постоянной.
Слайд 47х
Уравнение Шредингера для стационарных состояний
можно переписать в виде:
–
оператор Гамильтона,
равный сумме операторов
Гамильтониан
является оператором энергии E. 
Слайд 48х
В квантовой механике и другим динамическим переменным сопоставляются операторы.
Соответственно
рассматривают операторы координат, импульса, момента импульса и т.д.
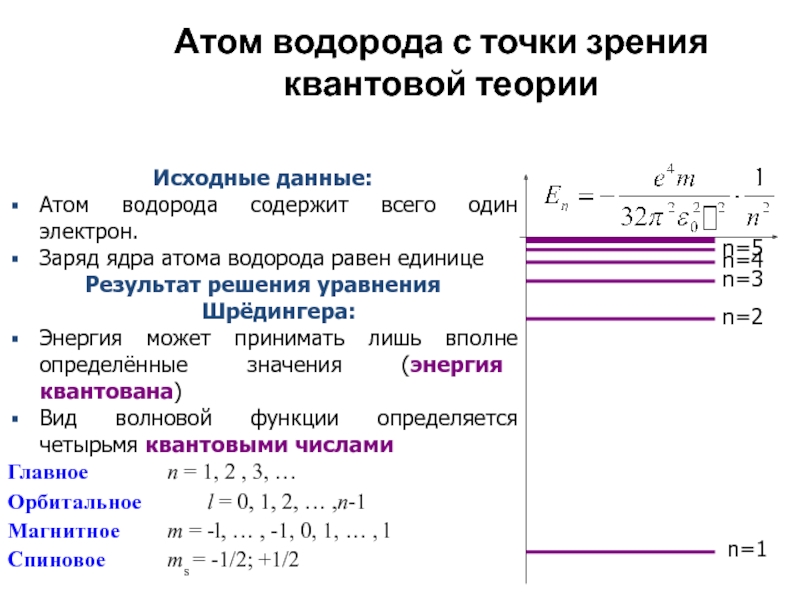
Слайд 51Атом водорода с точки зрения квантовой теории
Исходные данные:
Атом водорода содержит
всего один электрон.
Заряд ядра атома водорода равен единице
Результат решения уравнения
Шрёдингера:Энергия может принимать лишь вполне определённые значения (энергия квантована)
Вид волновой функции определяется четырьмя квантовыми числами
Главное n = 1, 2 , 3, …
Орбитальное l = 0, 1, 2, … ,n-1
Магнитное m = -l, … , -1, 0, 1, … , l
Спиновое ms = -1/2; +1/2
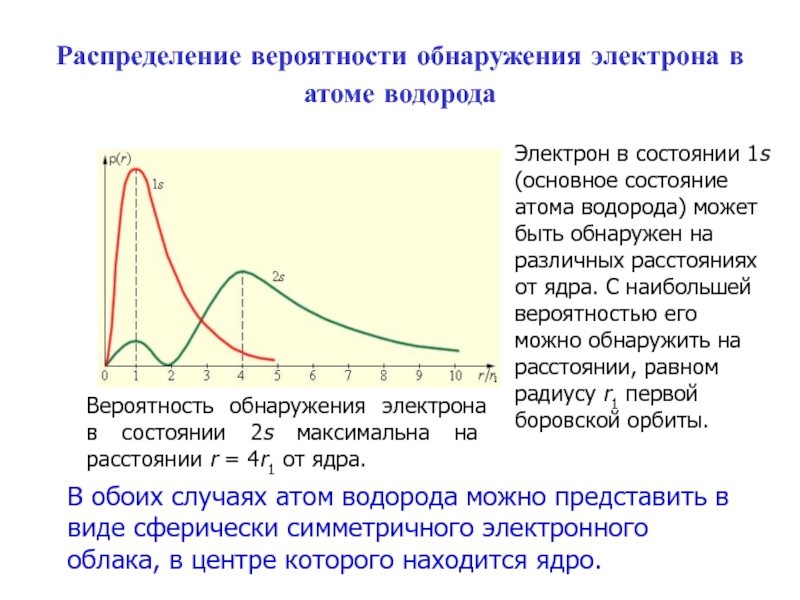
Слайд 53Распределение вероятности обнаружения электрона в атоме водорода
В обоих случаях
атом водорода можно представить в виде сферически симметричного электронного облака,
в центре которого находится ядро.Электрон в состоянии 1s (основное состояние атома водорода) может быть обнаружен на различных расстояниях от ядра. С наибольшей вероятностью его можно обнаружить на расстоянии, равном радиусу r1 первой боровской орбиты.
Вероятность обнаружения электрона в состоянии 2s максимальна на расстоянии r = 4r1 от ядра.
Слайд 54Возбуждённое состояние, n=3
Некоторые из возможных форм электронного облака в атоме
водорода
Основное состояние, n=1
Возбуждённые состояния, n=2
Возбуждённые состояния, n=4
