Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрическая вероятность
Содержание
- 1. Геометрическая вероятность
- 2.
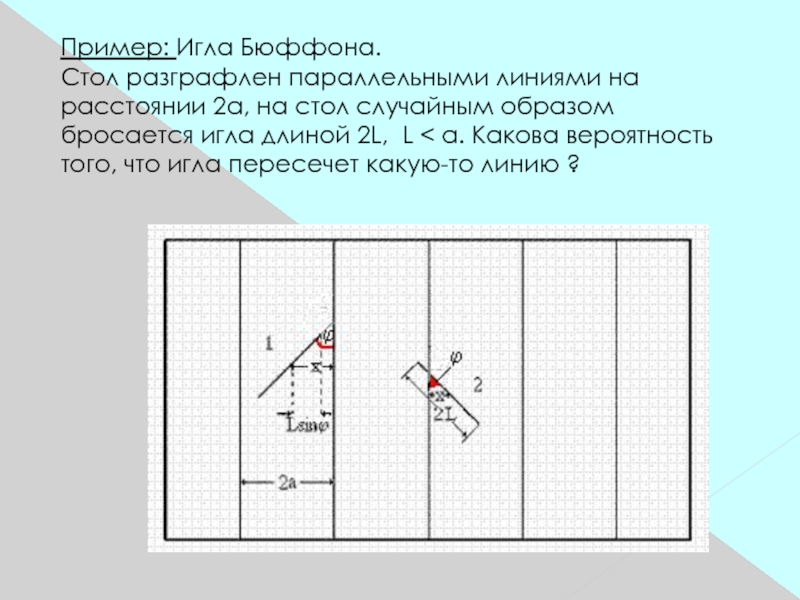
- 3. Пример: Игла Бюффона. Стол разграфлен параллельными линиями на
- 4. Положение иглы можно характеризовать двумя
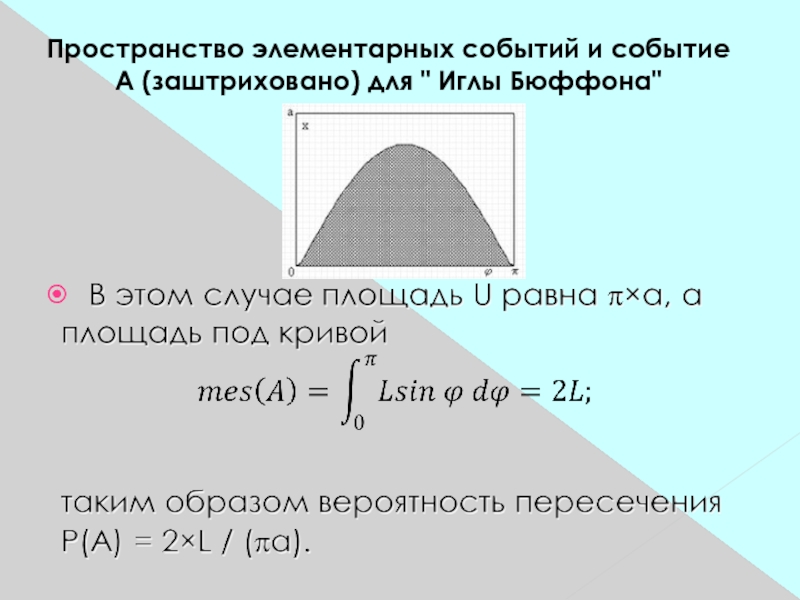
- 5. Пространство элементарных событий и событие А (заштриховано) для " Иглы Бюффона"
- 6. Задача о встрече «Дуэли в городе N
- 7. Вероятность зависит от выбора пространства элементарных событийНа
- 8. Вероятность зависит от выбора пространства элементарных событийНа
- 9. УСЛОВНАЯ ВЕРОЯТНОСТЬ НЕЗАВИСИМЫЕ СОБЫТИЯ ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И ВЕРОЯТНОСТИ ГИПОТЕЗ
- 10. Если события А и В
- 11. Пример : Пусть в области,
- 12. Если P(A/B) = P(A), то события А и
- 13. Формула полной вероятности Пусть событие А
- 14. Пример1: Магазин закупает оптом
- 15. Пример2: Петя и Коля
- 16. Доля выигрышей у комбинаций , стоящих в верхней строке по сравнению с комбинацией в столбце.
- 17. Формула вероятности гипотез В предыдущем примере
- 18. Пример 3: Студент приходит в медпункт
- 19. Эксперимент, результат которого существенно изменяет априорные
- 20. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- 21. Строго понятие "случайная величина" определяется так:
- 22. В строгом определении
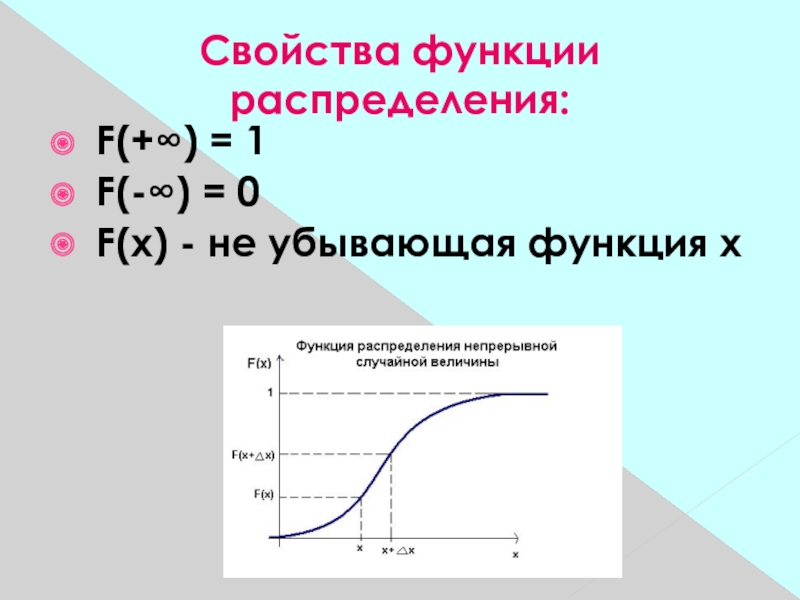
- 23. Свойства функции распределения: F(+∞) = 1 F(-∞) = 0 F(x) - не убывающая функция х
- 24. Случайные
- 25. Пример: число очков
- 26. Для непрерывных случайных величин вводится понятие
- 27. Для непрерывных распределений
- 28. ТИПИЧНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
- 29. Вид функций F(x),
- 30. Во-вторых, очень часто
- 31. 1 . Равномерное распределение Так называют
- 32. 2 . Нормальное распределениеРаспределение с плотностью, описываемой формулойназывается нормальным. Параметры распределения: a , σ
- 33. 3 . Распределение БернуллиЕсли производится серия n независимых испытаний,
- 34. Пример : Кость бросают 5 раз,
- 35. 4 . Распределение ПуассонаПараметр распределения: a Распределению Пуассона подчиняются
- 36. Пример1 : число
- 37. Пример 2:
- 38. Числовые характеристики случайных величин
- 39. 1 . Математическое ожидание (среднее значение)Определение: Математическим ожиданием называется
- 40. - для непрерывной случайной величины:Интеграл должен быть абсолютно
- 41. Свойства математического ожидания: a .
- 42. Свойства математического ожидания: d. Вводится понятие условного
- 43. Если известны вероятности событий
- 44. Рассмотрим гипотезы Н1 - герб выпал в первыйже
- 45. Рассмотрим более общий случай: сколькопройдет испытаний до
- 46. e . Если f(x) - есть функция случайной
- 47. 2 . Дисперсия случайной величины Определение: Дисперсией
- 48. - для непрерывной случайной величины: Интеграл должен быть
- 49. Свойства дисперсии: a . Если
- 50. Связь числовых характеристик с параметрами законов распределенияРаспределение
- 51. Связь числовых характеристик и параметров типичных распределений
- 52. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4 Положение иглы можно характеризовать двумя параметрами: Х - расстояние от центра
иглы до ближайшей линии, φ - угол между направлением иглы и линии.
"Случайность" положения иглы означает, что Х может равновероятно принимать любые значения от 0 до а, а φ - соответственно - от 0 до π. Тогда пространство элементарных событий представим прямоугольником, а событие А (пересечение произошло) - областью под кривой Х = L×sinφ, т.к. для пересечения нужно, чтобы Х было меньше, чем L×sinφ.
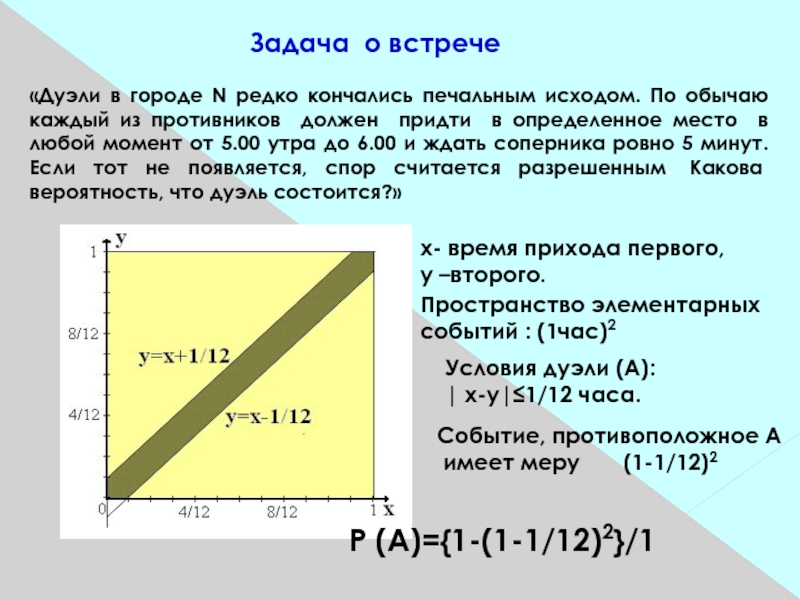
Слайд 6Задача о встрече
«Дуэли в городе N редко кончались печальным
исходом. По обычаю каждый из противников должен придти в определенное
место в любой момент от 5.00 утра до 6.00 и ждать соперника ровно 5 минут. Если тот не появляется, спор считается разрешенным. Какова вероятность, что дуэль состоится?»х- время прихода первого,
у –второго.
Пространство элементарных
событий : (1час)2
Условия дуэли (А):
| х-у|≤1/12 часа.
Событие, противоположное А
имеет меру (1-1/12)2
Р (А)={1-(1-1/12)2}/1
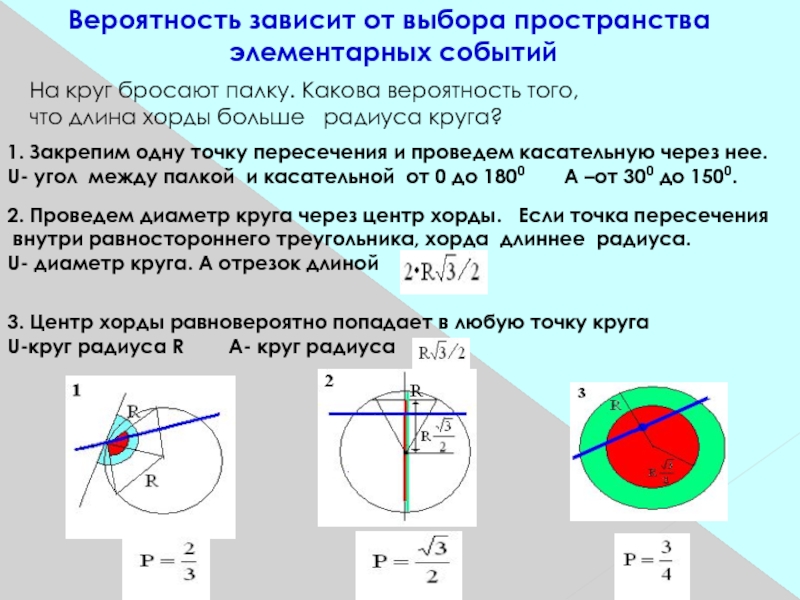
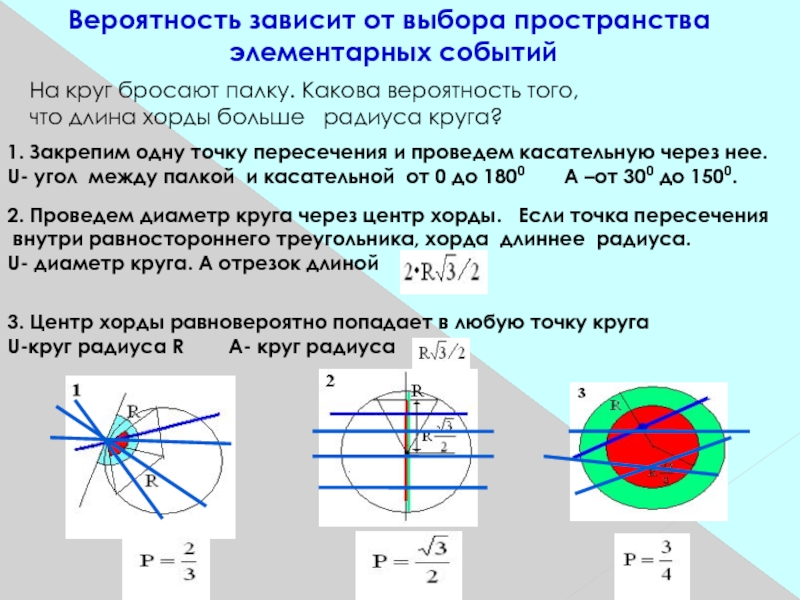
Слайд 7Вероятность зависит от выбора пространства
элементарных событий
На круг бросают палку.
Какова вероятность того,
что длина хорды больше радиуса круга?
1.
Закрепим одну точку пересечения и проведем касательную через нее.U- угол между палкой и касательной от 0 до 1800 А –от 300 до 1500.
2. Проведем диаметр круга через центр хорды. Если точка пересечения
внутри равностороннего треугольника, хорда длиннее радиуса.
U- диаметр круга. А отрезок длиной
3. Центр хорды равновероятно попадает в любую точку круга
U-круг радиуса R А- круг радиуса
Слайд 8Вероятность зависит от выбора пространства
элементарных событий
На круг бросают палку.
Какова вероятность того,
что длина хорды больше радиуса круга?
1.
Закрепим одну точку пересечения и проведем касательную через нее.U- угол между палкой и касательной от 0 до 1800 А –от 300 до 1500.
2. Проведем диаметр круга через центр хорды. Если точка пересечения
внутри равностороннего треугольника, хорда длиннее радиуса.
U- диаметр круга. А отрезок длиной
3. Центр хорды равновероятно попадает в любую точку круга
U-круг радиуса R А- круг радиуса
Слайд 10 Если события А и В принадлежат одному полю
событий и вероятность В не равна 0, то условной вероятностью
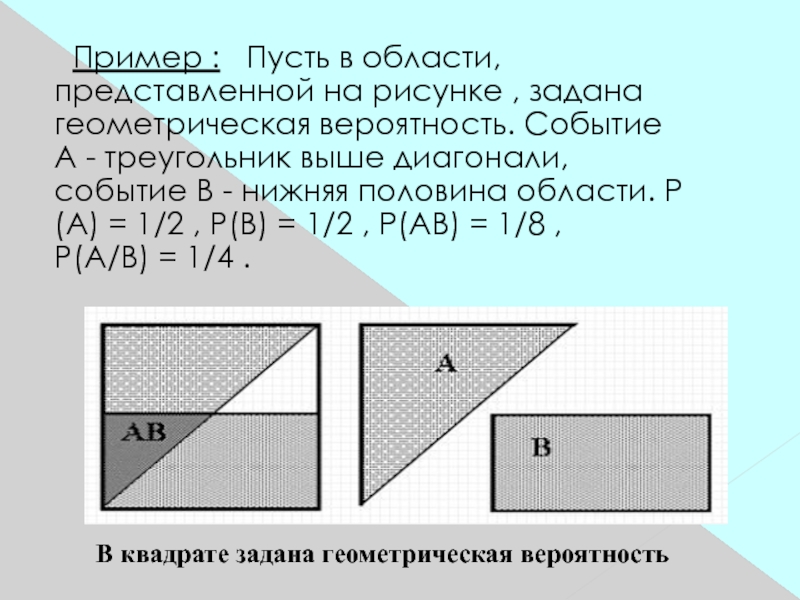
А при условии В называется отношение вероятности пересечения А и В к вероятности В.Слайд 11 Пример : Пусть в области, представленной на рисунке
, задана геометрическая вероятность. Событие А - треугольник выше диагонали, событие В - нижняя
половина области. Р(А) = 1/2 , Р(В) = 1/2 , Р(АВ) = 1/8 , P(A/B) = 1/4 .В квадрате задана геометрическая вероятность
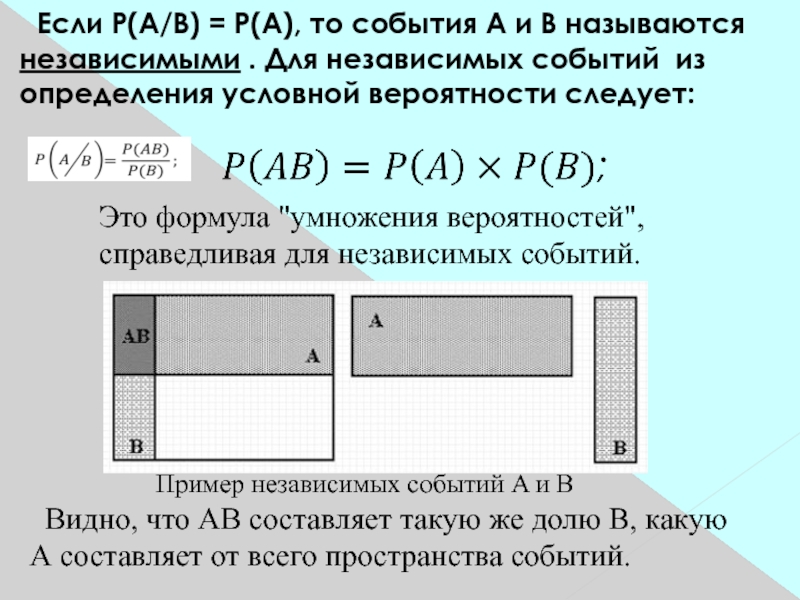
Слайд 12 Если P(A/B) = P(A), то события А и В называются независимыми
. Для независимых событий из определения условной вероятности следует:
Это
формула "умножения вероятностей", справедливая для независимых событий.Пример независимых событий A и В
Видно, что АВ составляет такую же долю В, какую А составляет от всего пространства событий.
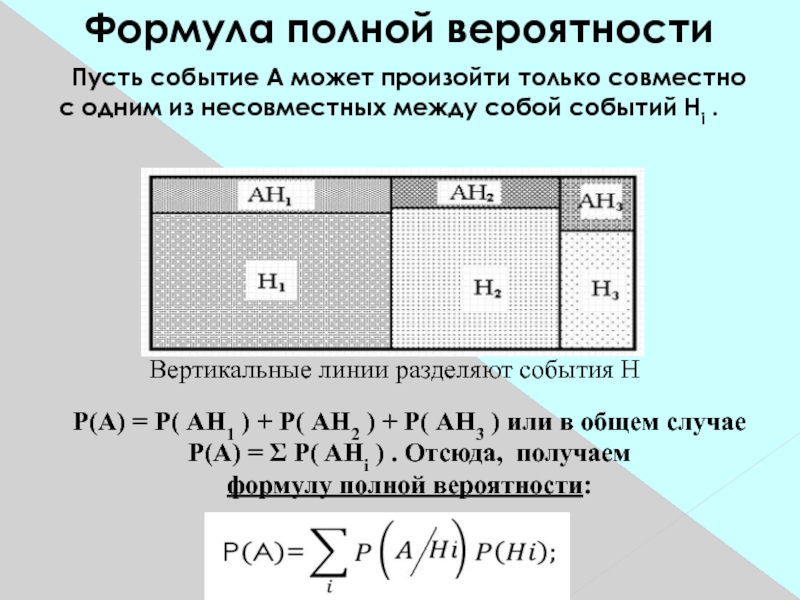
Слайд 13Формула полной вероятности
Пусть событие А может произойти только совместно
с одним из несовместных между собой событий Hi .
Вертикальные
линии разделяют события H Р(А) = Р( АН1 ) + Р( АН2 ) + Р( АН3 ) или в общем случае P(A) = Σ P( AHi ) . Отсюда, получаем
формулу полной вероятности:
Слайд 14 Пример1: Магазин закупает оптом половину всех компьютеров
у фирмы LLL, треть - у фирмы МММ и 1/6
- у фирмы NNN. У фирмы LLL 10% компьютеров с браком, у фирмы МММ брак составляет 5%, а у фирмы NNN - 15%. Какова вероятность того, что наудачу выбранный компьютер в этом магазине - бракованный ? Дано: Р(Н1) = 1/2,Р(Н2) = 1/3, Р(Н3) = 1/6,
Р(А/Н1) = 0.1,
Р(А/Н2) = 0.05,
Р(А/Н3) = 0.15.
Получаем:
P(A)=0.1*1/2+0.05*1/3+
0.15*1/6=0.092
Слайд 15Пример2: Петя и Коля играют в монету
на
следующих условиях: монета бросается до тех пор,
пока серия
бросков не закончится выбранной игроком парой, тогда он выигрывает. Если Петя
выбрал ГГ, а Коля РР, очевидно, вероятности
выигрышей одинаковы. А если Петя –ГГ, а Коля- РГ?
Например: ГГ- Петя выиграл, РРРРГ- Коля выиграл.
Вычислим вероятность выигрыша Пети с помощью
формулы полной вероятности , используя гипотезы:
Н1- первый бросок-герб, Н2- первый бросок-решка.
Р(ГГ)=Р(ГГ/Н1)Р(Н1)+Р(ГГ/Н2)Р(Н2)=
½ * ½ + 0* ½ =1/4
Если игроки задумывают не 2 , а 3 конечных броска,
Например: РГРГРРГГ- Петя выиграл;
ГРГГГГР- Коля выиграл.
На каждую тройку результатов есть более выигрышная.
Слайд 16Доля выигрышей у комбинаций , стоящих в верхней
строке по
сравнению с комбинацией в столбце.
Слайд 17Формула вероятности гипотез
В предыдущем примере можно поставить и другой
вопрос. Обнаружен компьютер с браком, какова вероятность, что он получен
от фирмы NNN ? Т.е. зная вероятности Р(Нi), которые называются априорные вероятности гипотез Нi, и условные вероятности Р(А/Нi) события А при каждой гипотезе, мы хотим найти апостериорную вероятность Р(Нi/А) i-той гипотезы при условии, что событие А произошло:Заменив знаменатель формулой полной вероятности , получаем:
Слайд 18 Пример 3: Студент приходит в медпункт и жалуется на
плохое самочувствие, хотя по виду этого не скажешь. У медсестры
две гипотезы Н1 - он действительно болен, Н2 - он здоров, но хочет получить справку, например, для продления сессии. По внешнему виду она оценивает априорные вероятности Р(Н1) = 0.3, Р(Н2) = 0.7 и ставит ему градусник. Измеренная температура 37.5 (событие А). Предположим, Р(А/Н1) = 0.9 (не при всякой болезни повышается температура), Р(А/Н2) = 0.05 (у некоторых здоровых людей нормальная температура немного повышена или студент мог незаметно натереть градусник). Теперь апостериорнаявероятность того, что студент
болен:
У медсестры есть все основания направить студента к врачу.
Слайд 19 Эксперимент, результат которого существенно изменяет априорные вероятности гипотез, называют
информативным. Перед постановкой сложного и (или) дорогостоящего эксперимента всегда имеет
смысл оценить его информативность на основе имеющихся данных об априорных и условных вероятностях.Слайд 21Строго понятие "случайная величина" определяется так:
Пусть имеется пространство
элементарных событий U,
на нем построено поле событий и для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному событию gi из U сопоставим число ξi. Потребуем, чтобы для любого х (-∞ < x < +∞) множество А тех g, для которых ξ < x , принадлежало полю событий, т.е. для него определена вероятность Р{ξ < x} = P(A) = F(x). Тогда ξ называется случайной величиной, а F(x) - ее функцией распределения.
Слайд 22 В строгом определении задание пространства элементарных
событий означает по существу задание условий, в которых возникают те
или иные значения случайной величины, а если эти условия заданы, то тем самым определена и F(x).Например, нельзя сказать, что "температура - случайная величина". Но "температура воздуха, измеряемая на данной метеостанции в случайный момент времени в течение года" - случайная величина, "температура воздуха в случайно выбранной точке земного шара 1 января 2001г. в 12.00 по Московскому времени" - другая случайная величина.
Слайд 24 Случайные величины могут быть
непрерывными, т.е. принимать любые значения в некотором интервале (например, упомянутые
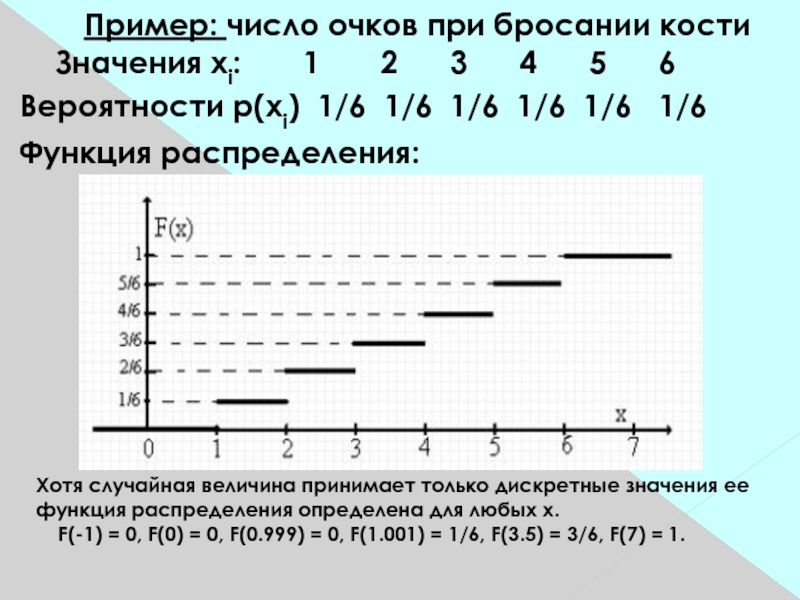
выше температуры). У них F(x) - непрерывная функция. Случайные величины могут быть дискретными т.е. принимать только конечное или счетное множество определенных значений (например, число очков при бросании игральной кости; число телефонных звонков, поступающих конкретному абоненту в течение суток). У таких величин F(x) имеет разрывы в точках, соответствующих принимаемым значениям. Такие величины удобнее характеризовать указанием возможных значений и их вероятностей.Слайд 25 Пример: число очков при бросании кости
Значения хi: 1
2 3 4 5 6Вероятности р(хi) 1/6 1/6 1/6 1/6 1/6 1/6
Функция распределения:
Хотя случайная величина принимает только дискретные значения ее функция распределения определена для любых х.
F(-1) = 0, F(0) = 0, F(0.999) = 0, F(1.001) = 1/6, F(3.5) = 3/6, F(7) = 1.
Слайд 26 Для непрерывных случайных величин вводится понятие плотности распределения р(х),
которая есть производная от функции распределения.
Вероятность того, что случайная
величина ξ примет значение, лежащее в интервале (а,b) равна разности
значений функции распределения на концах
интервала
Для непрерывных случайных величин
Слайд 27 Для непрерывных распределений всегда
Для дискретных
распределений
сумма р(хi) по всем возможным значениям хi
всегда равна
1;Слайд 29 Вид функций F(x), р(х), или перечисление
р(хi) называют законом распределения случайной величины.
Хотя можно представить себе
бесконечное разнообразие случайных величин, законов распределения гораздо меньше. Во-первых, различные случайные величины могут иметь совершенно одинаковые законы распределения.Например: пусть y принимает всего 2 значения 1 и -1 с вероятностями 0.5; величина z = -y имеет точно такой же закон распределения.
Слайд 30 Во-вторых, очень часто случайные величины имеют
подобные законы распределения, т.е., например, р(х) для них выражается формулами
одинакового вида, отличающимися только одной или несколькими постоянными. Эти постоянные называются параметрами распределения.Хотя в принципе возможны самые разные законы распределения, обычно рассматривают несколько наиболее типичных законов. Важно обратить внимание на условия, в которых они возникают, параметры и свойства этих распределений.
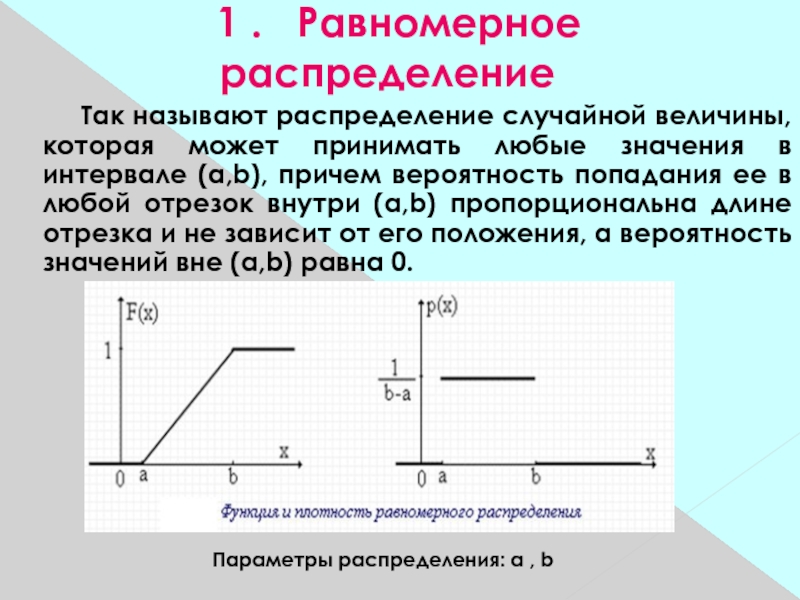
Слайд 31 1 . Равномерное распределение
Так называют распределение случайной величины,
которая может принимать любые значения в интервале (a,b), причем вероятность
попадания ее в любой отрезок внутри (a,b) пропорциональна длине отрезка и не зависит от его положения, а вероятность значений вне (a,b) равна 0.Параметры распределения: a , b
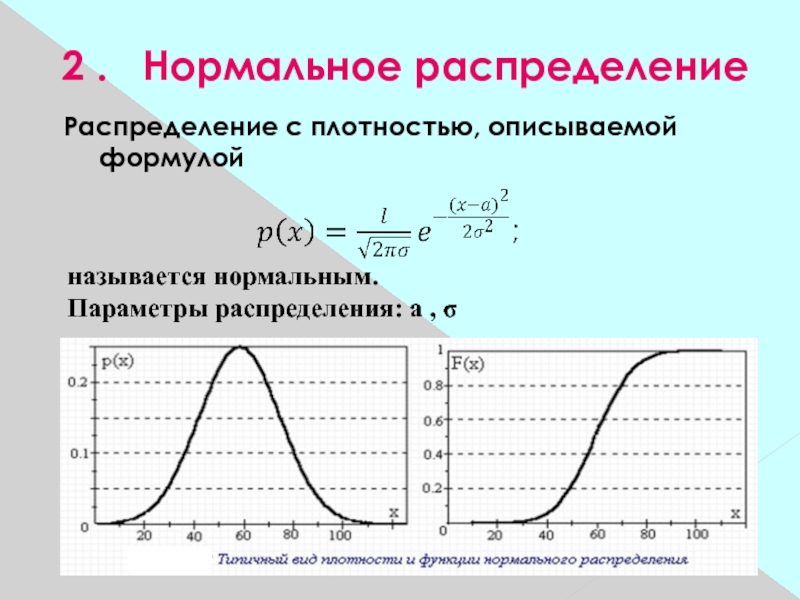
Слайд 32 2 . Нормальное распределение
Распределение с плотностью, описываемой формулой
называется нормальным.
Параметры распределения: a ,
σ
Слайд 33 3 . Распределение Бернулли
Если производится серия n независимых испытаний, в каждом из
который событие А может появиться с одинаковой вероятностью р, то
число m появлений события есть случайная величина.Один возможный исход серии n независимых испытаний :
и он имеет вероятность
где q=1-p
Исходы, при которых А произошло в разные моменты испытаний,
несовместны и число таких вариантов ,поэтому
Распределение называется распределением Бернулли,
или биномиальным распределением
Его параметры n и p
Слайд 34Пример : Кость бросают 5 раз, какова вероятность того,
что 6 очков выпадет дважды ?
n = 5,
m = 2,
p = 1/6, q = 5/6
Слайд 354 . Распределение Пуассона
Параметр распределения: a
Распределению Пуассона подчиняются очень многие случайные
величины, встречающиеся в науке и практической жизни.
Распределение Пуассона получается
как предельный случай распределения Бернулли, если устремить р к нулю, а n к бесконечности, но так, чтобы их произведение оставалось постоянным: nр = а. (p=a/n)P(m)=
Слайд 36 Пример1 : число вызовов, поступающих на
станцию скорой помощи в течение часа. Разобьем интервал времени
Т (1 час) на малые интервалы dt, такие что вероятность поступления двух и более вызовов в течение dt пренебрежимо мала, а вероятность одного вызова р пропорциональна dt: р = μdt ; будем рассматривать наблюдение в течение моментов dt как независимые испытания, число таких испытаний за время Т: n = T / dt. Если предполагать, что вероятности поступления вызовов не меняются в течение часа, то полное число вызовов подчиняется закону Бернулли с параметрами: n = T / dt, р = μdt . Устремив dt к нулю, получим, что n стремится к бесконечности, а произведение n×р остается постоянным: а = n×р = μТ.Слайд 37 Пример 2: число молекул идеального
газа в некотором фиксированном объеме V. Разобьем объем
V на малые объемы dV такие, что вероятность нахождения двух и более молекул в dV пренебрежимо мала, а вероятность нахождения одной молекулы пропорциональна dV: р = μdV; будем рассматривать наблюдение каждого объемчика dV как независимое испытание, число таких испытаний n=V/dV; если предполагать, что вероятности нахождения молекулы в любом месте внутри V одинаковы, полное число молекул в объеме V подчиняется закону Бернулли с параметрами: n = V / dV, р = μdV. Устремив dV к нулю, получим, что n стремится к бесконечности, а произведение n×р остается постоянным: а = n×р =μV.Слайд 39 1 . Математическое ожидание (среднее значение)
Определение:
Математическим ожиданием называется
- для дискретной случайной величины:
Сумма берется
по всем значениям, которые принимает случайная величина. Ряд должен быть
абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)
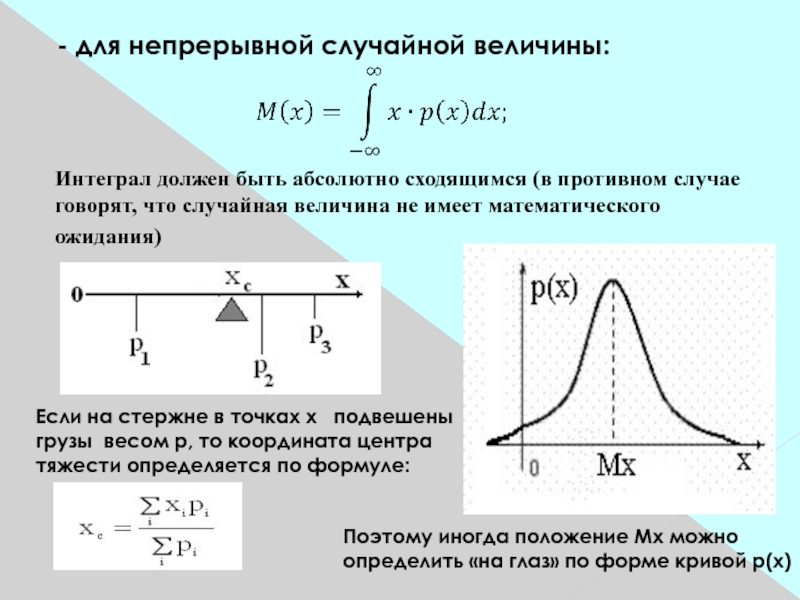
Слайд 40- для непрерывной случайной величины:
Интеграл должен быть абсолютно сходящимся (в противном
случае говорят, что случайная величина не имеет математического ожидания)
Если
на стержне в точках х подвешены грузы весом р, то координата центра тяжести определяется по формуле:Поэтому иногда положение Мх можно
определить «на глаз» по форме кривой р(х)
Слайд 41Свойства математического ожидания:
a . Если С - постоянная
величина, то МС = С b . МСх = СМх c . Математическое ожидание суммы случайных
величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + МyСлайд 42Свойства математического ожидания:
d. Вводится понятие условного математического ожидания. Если
случайная величина принимает свои значения хi с различными вероятностями p(xi/Hj)
при разных условиях Hj, то условное математическое ожидание определяется какСлайд 43 Если известны вероятности событий Hj, может быть
найдено полное математическое ожидание:
Пример: Сколько раз в среднем
надо бросать монету до первого выпадения герба ?
Слайд 44Рассмотрим гипотезы Н1 - герб выпал в первый
же раз, Н2 - в
первый раз он не выпал. Очевидно, р(Н1) = р(Н2) = ½; Мx / Н1 = 1;
Мx / Н2 на 1больше искомого полного матожидания, т.к.
после первого бросания монеты ситуация не
изменилась, но один раз она уже брошена.
Используя формулу полного математического
ожидания, имеем Мх = Мx / Н1×р(Н1) + Мx / Н2×р(Н2) =
1×0.5 + (Мх + 1)×0.5 ,
разрешая уравнение
относительно Мх,
получаем сразу Мх = 2 .
А сколько раз надо бросать монету до
десятого выпадения герба?
Слайд 45Рассмотрим более общий случай: сколько
пройдет испытаний до первого появления
события, если
его вероятность Р . Гипотеза Н1 -
оно появилось в первый
же раз, Н2 - в первый разоно не появилось. Очевидно, р(Н1) =Р,
р(Н2) = 1-Р; Мx / Н1 = 1; Мx / Н2 на 1 больше
искомого полного матожидания, т.к. После
первого испытания ситуация не изменилась, но
одно испытание уже сделано.
Используя формулу полного математического
ожидания, имеем Мх = Мx / Н1×р(Н1) + Мx / Н2×р(Н2) =
1×Р + (Мх + 1)×(1-Р)=P+Мх-Mx×P+1-P : -Mx ×P+1=0
разрешая уравнение относительно Мх,
получаем сразу Мх = 1/Р .
Слайд 46e . Если f(x) - есть функция случайной величины х, то
определено понятие математического ожидания функции случайной величины:
- для
дискретной случайной величины: Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.
-для непрерывной случайной величины:
Интеграл должен быть абсолютно сходящимся.
Слайд 47 2 . Дисперсия случайной величины
Определение: Дисперсией случайной величины х
называется математическое ожидание квадрата отклонения значения величины от ее математического
ожидания: Dx = M(x-Mx)2- для дискретной случайной величины:
Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)
Слайд 48- для непрерывной случайной величины:
Интеграл должен быть сходящимся (в противном
случае говорят, что случайная величина не имеет дисперсии)
Слайд 49Свойства дисперсии:
a . Если С - постоянная величина,
то DС = 0
b . DСх = С2Dх
c . Дисперсия суммы случайных величин равна
сумме их дисперсий только, если эти величины независимыd . Для вычисления дисперсии удобно использовать формулу:
Dx=M(x-Mx)2=M[x2-2xMx+(Mx)2]=Mx2-(Mx)2
Слайд 50Связь числовых характеристик
с параметрами законов распределения
Распределение Бернулли.
Введем случайную величину
ξ , равную 1 , если А произошло, и 0,
если не произошло , т.е.ξ=1 с вероятностью р и 0 с вероятностью (1-р).
Мξ=р. В серии из n независимых испытаний просуммировано n значений ξ. m=nξ, Mm=np.
Dξ=Mξ2-(Mξ)2=12*p-p2=p(1-p)=pq Dm=npq
Распределение Пуассона
np=a q~1
Mm=a Dm=a