TheSlide.ru

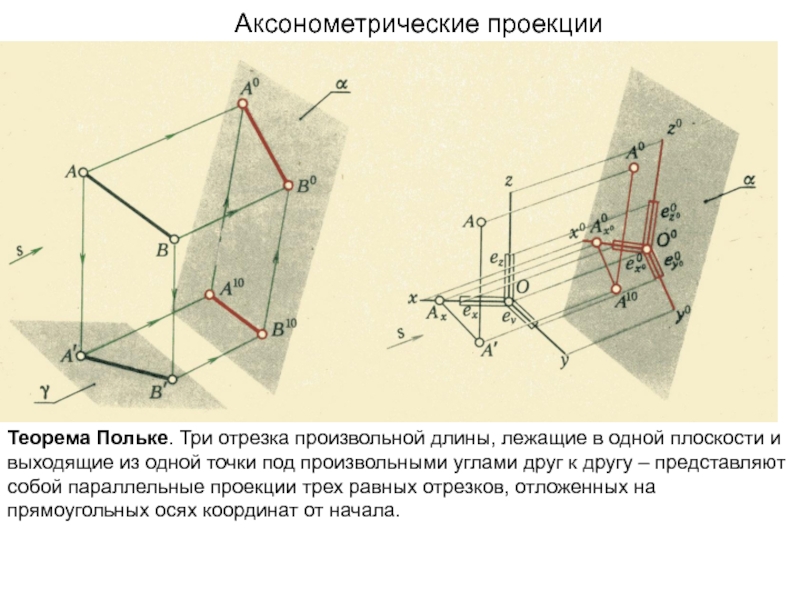
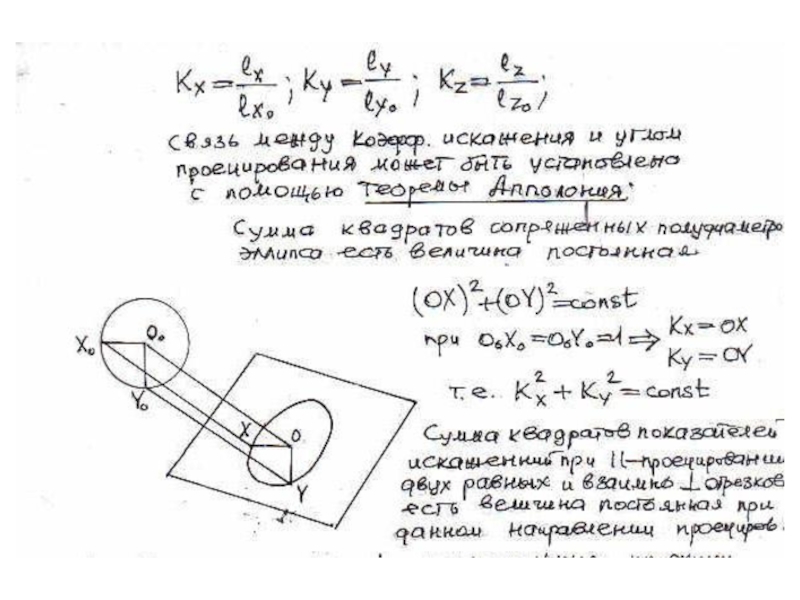
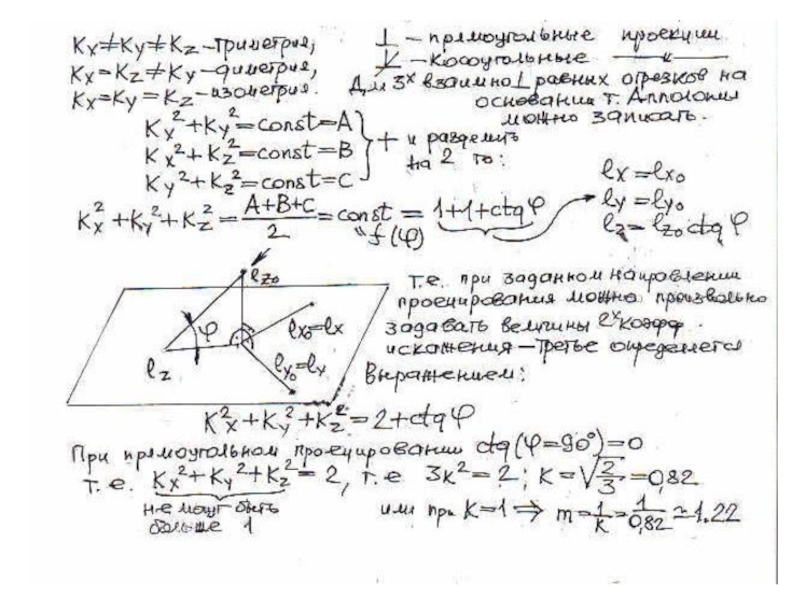
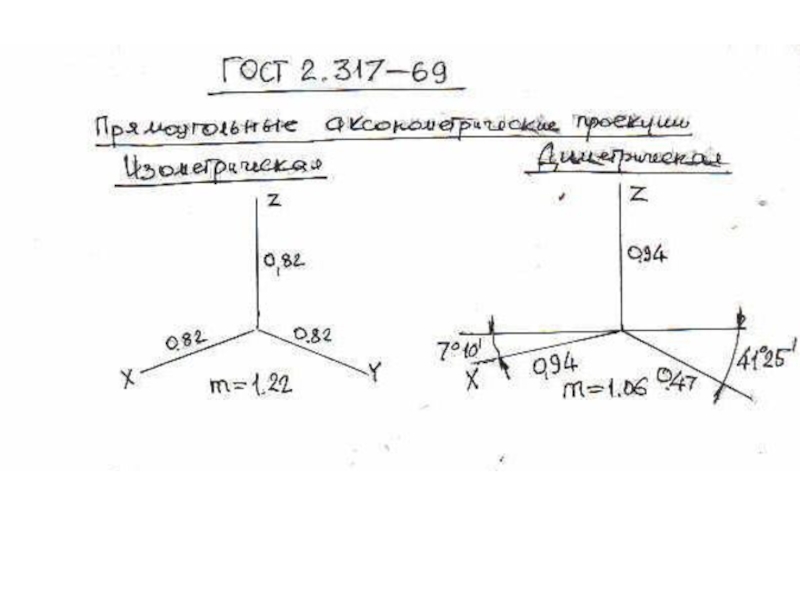
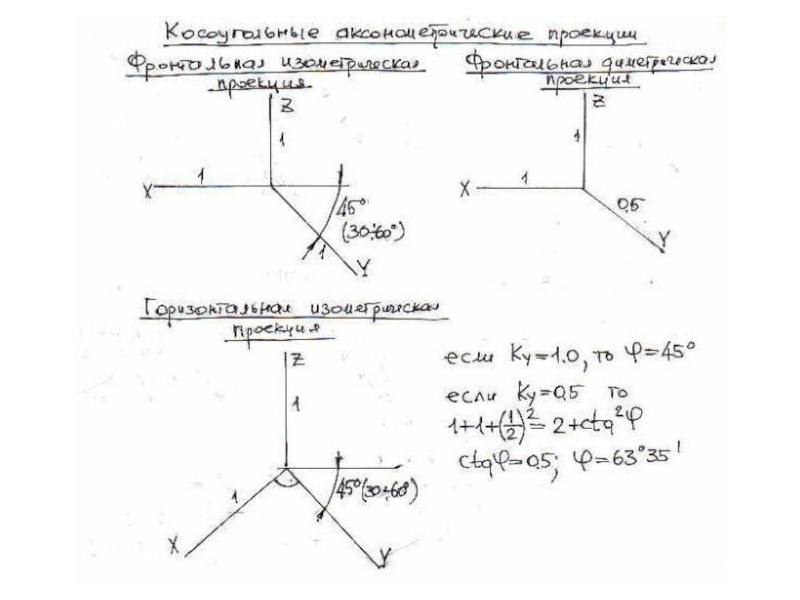
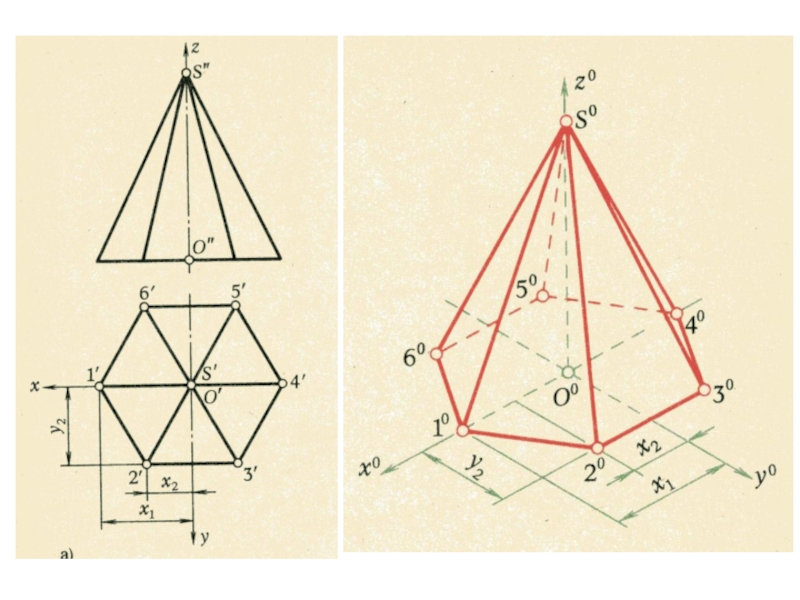
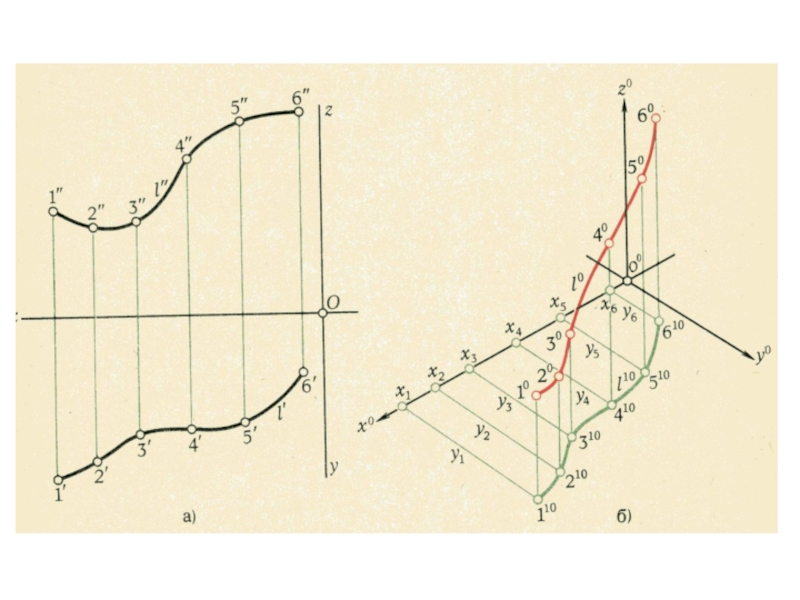
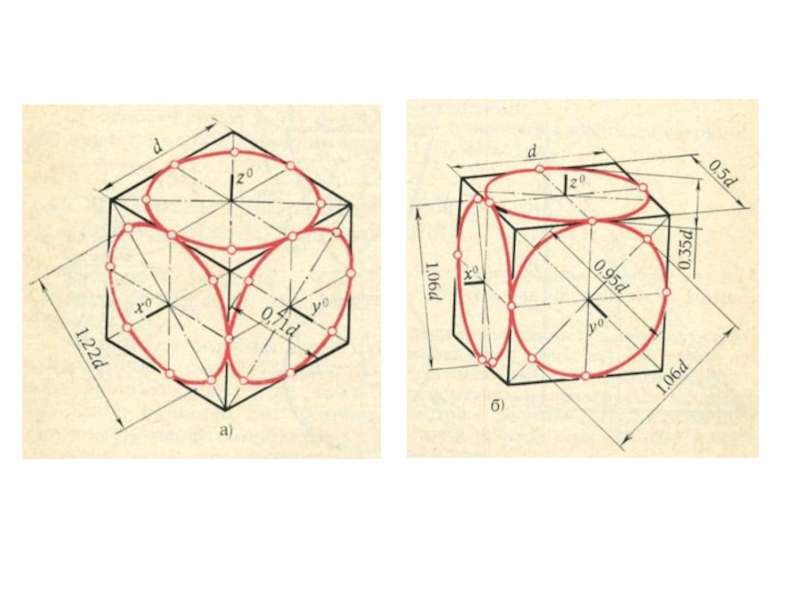
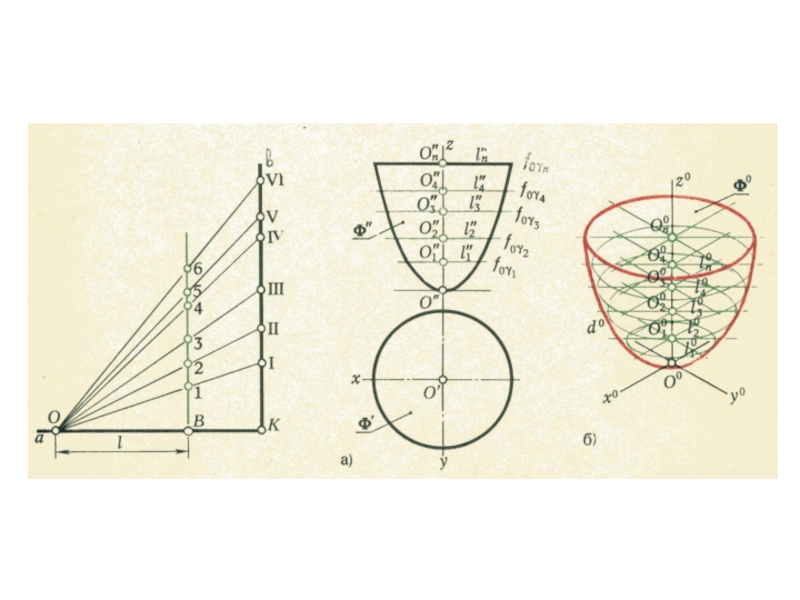
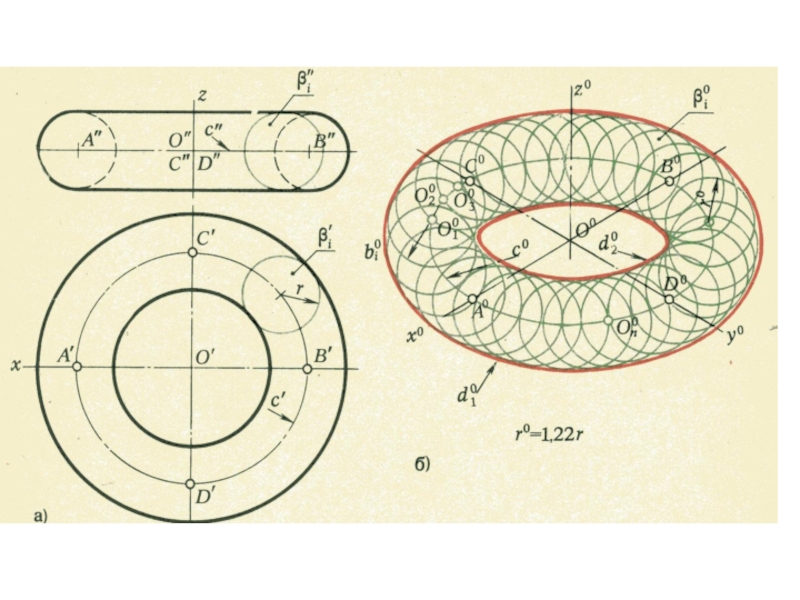
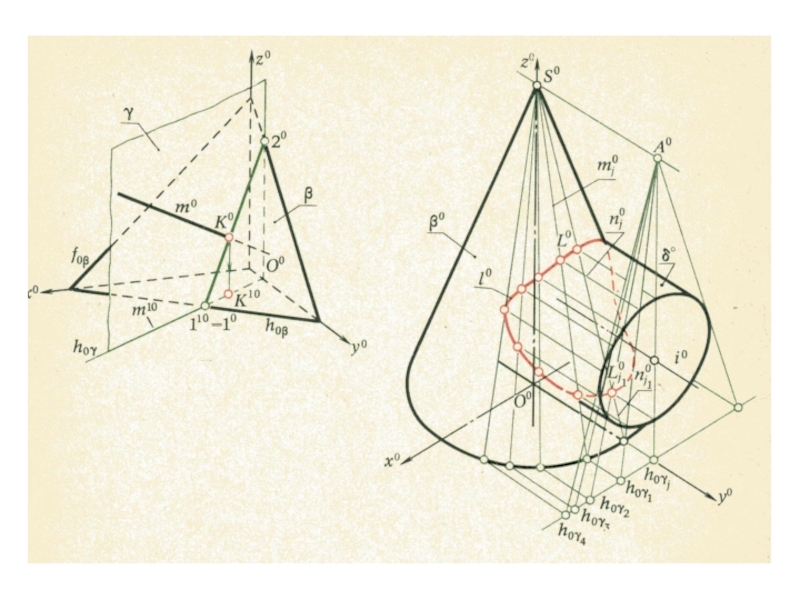
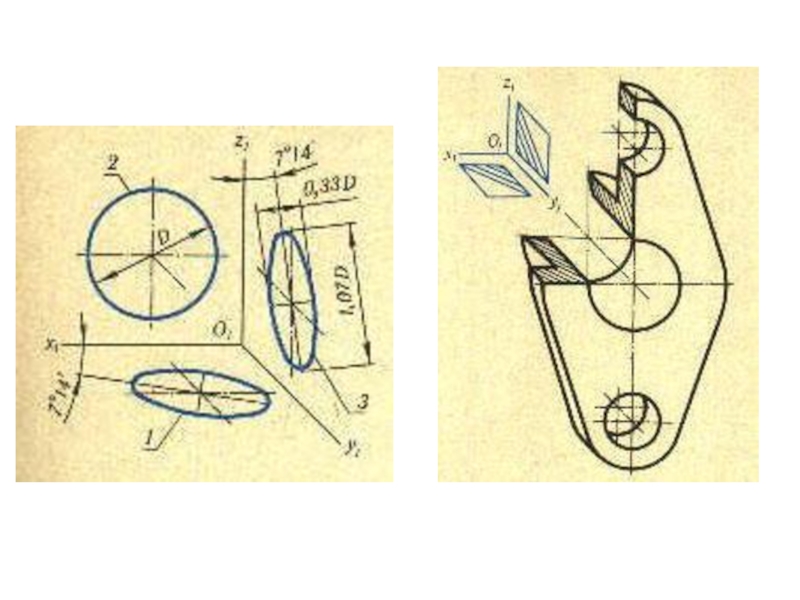
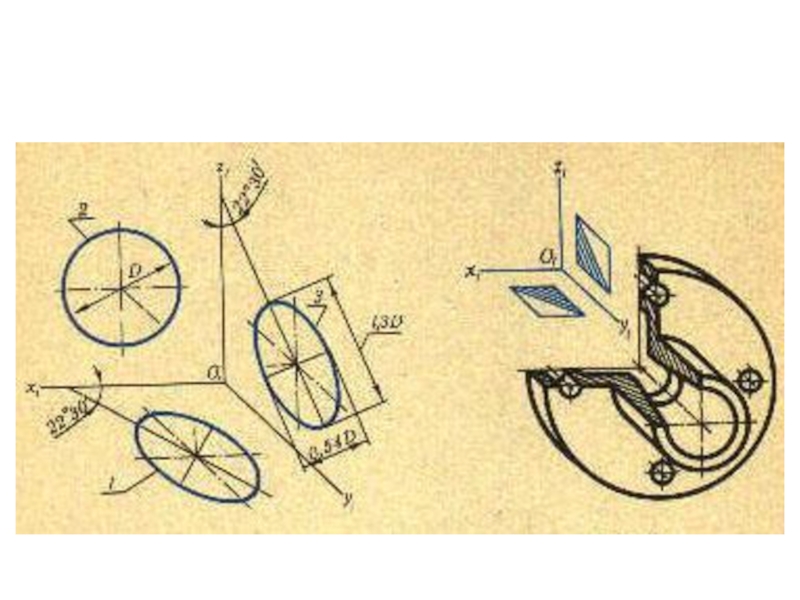
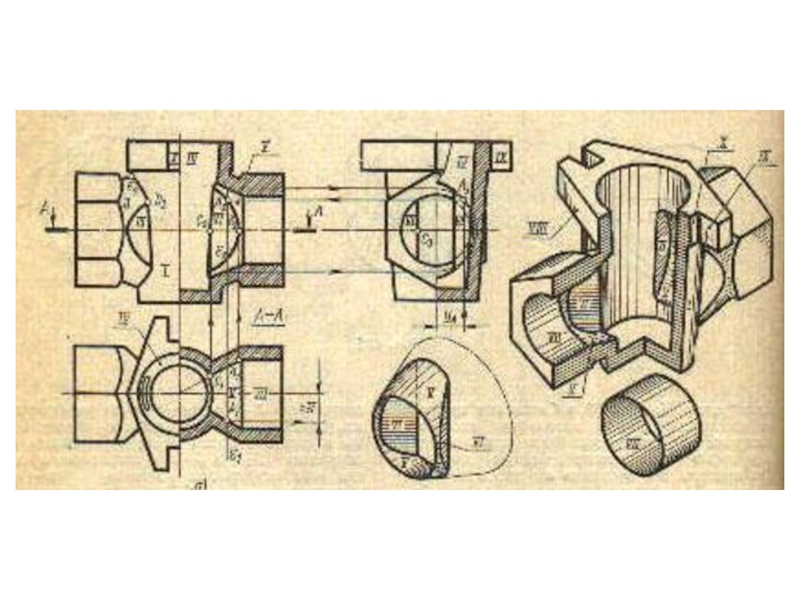
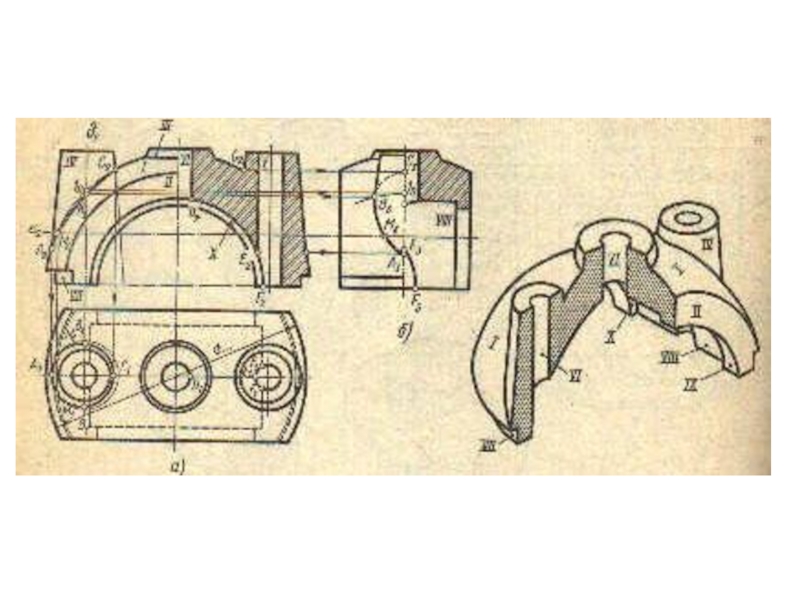
Аксонометрические проекции

Содержание

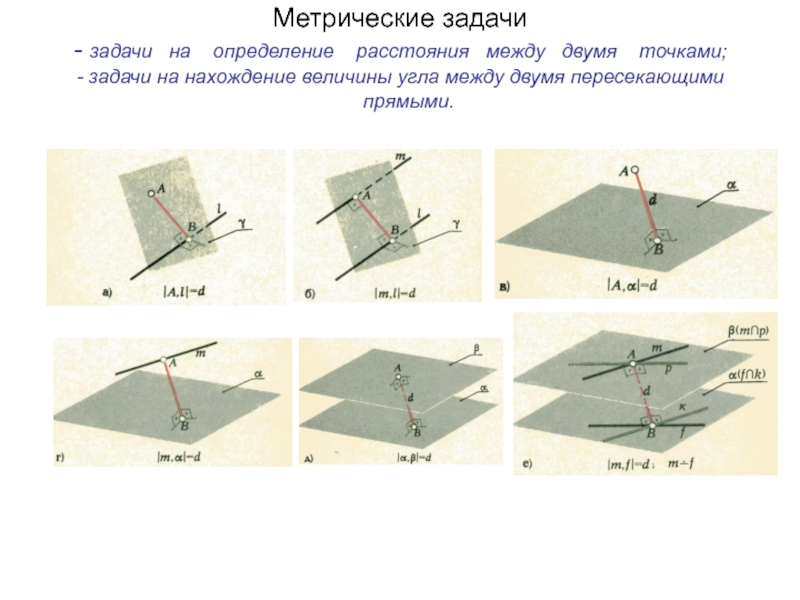
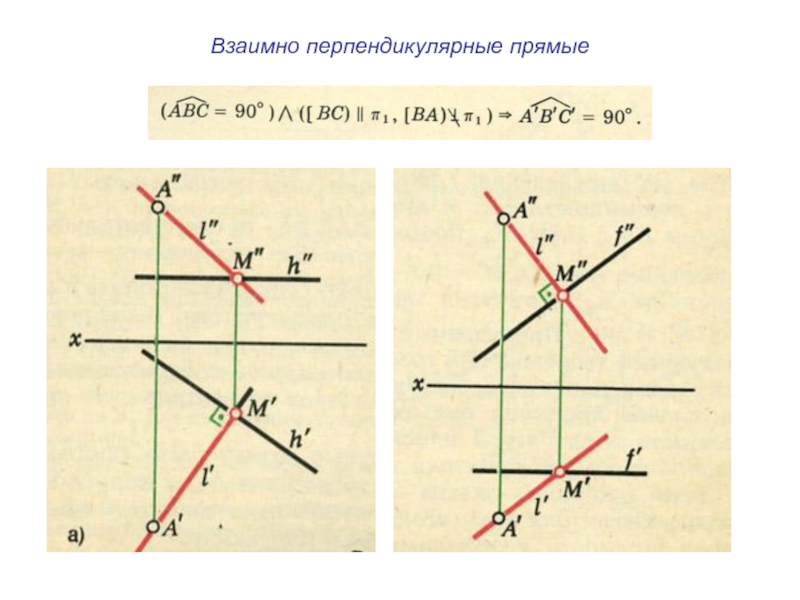
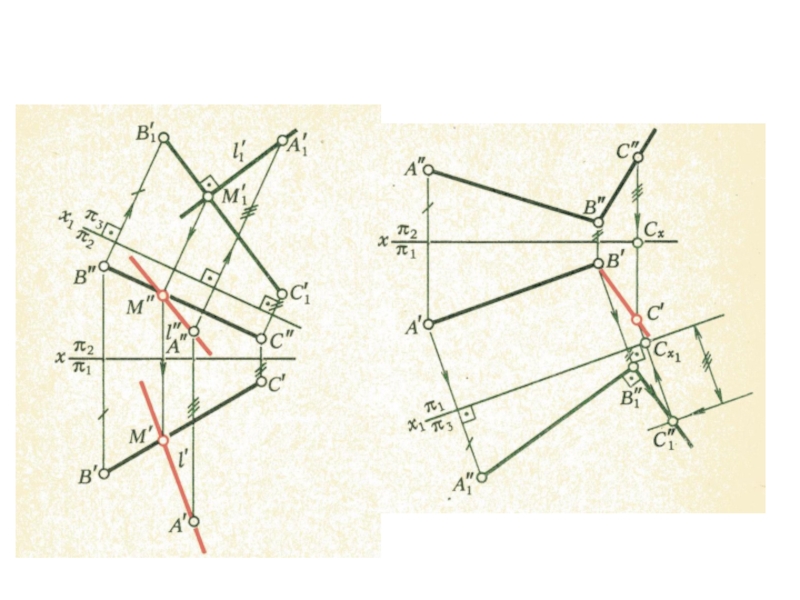
1. Аксонометрические проекции
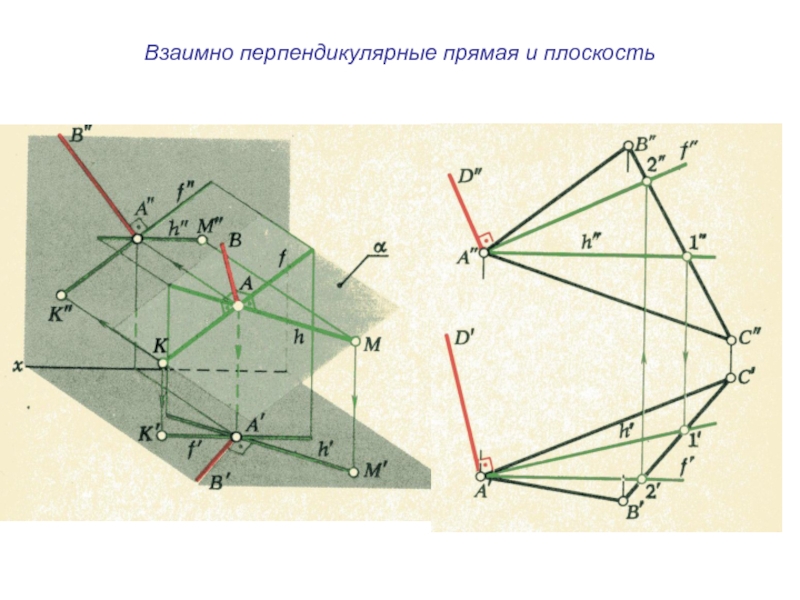
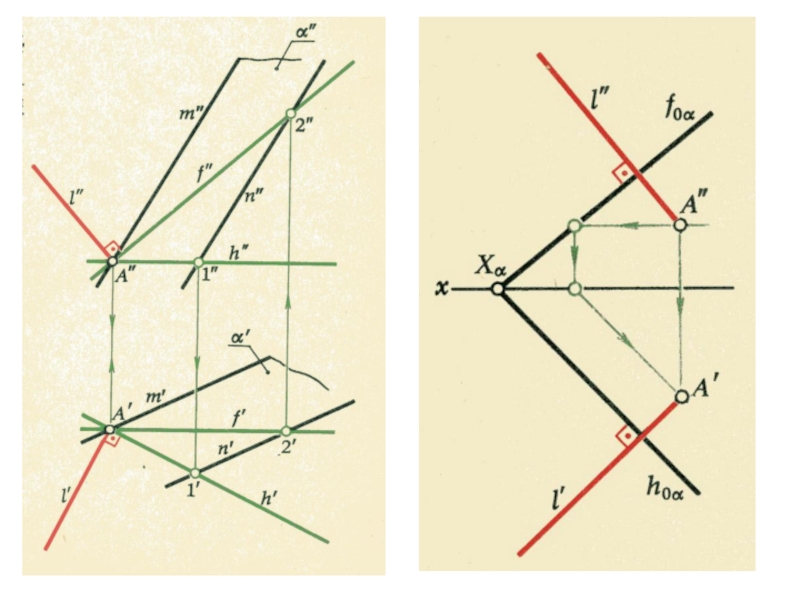
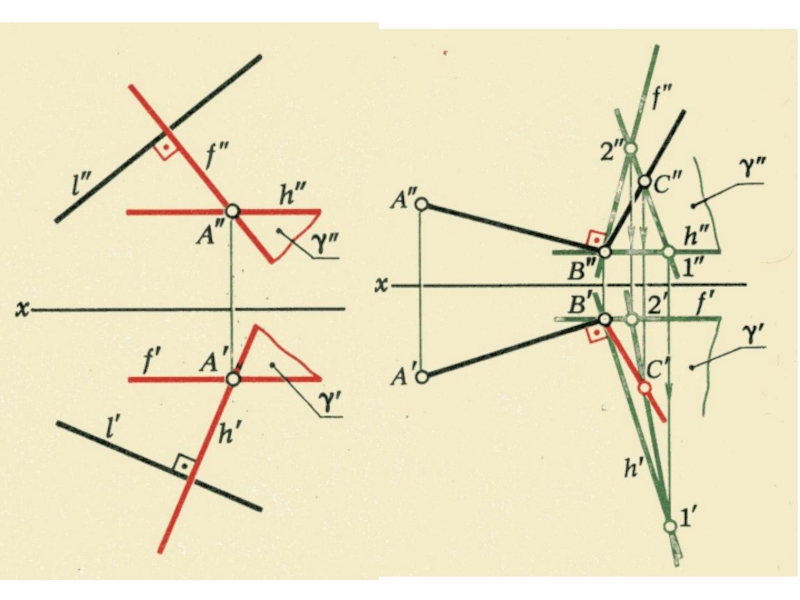
2. Аксонометрические проекции
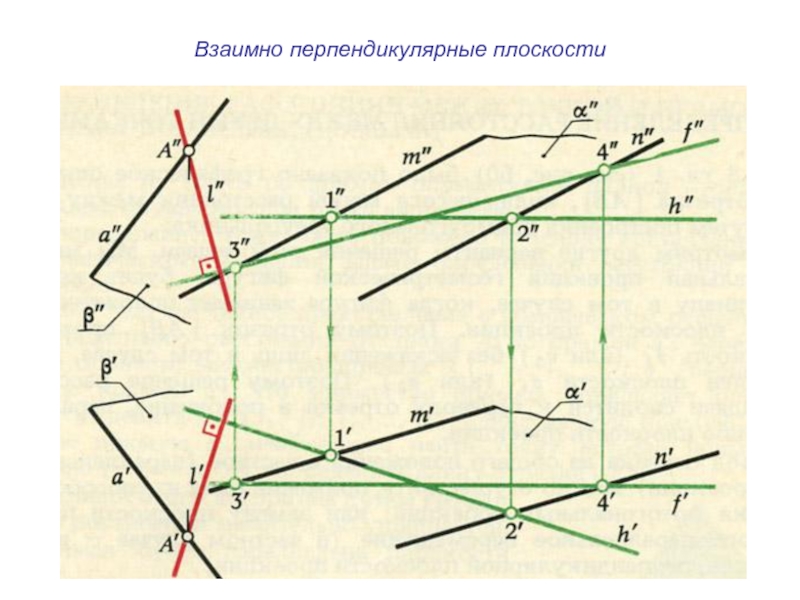
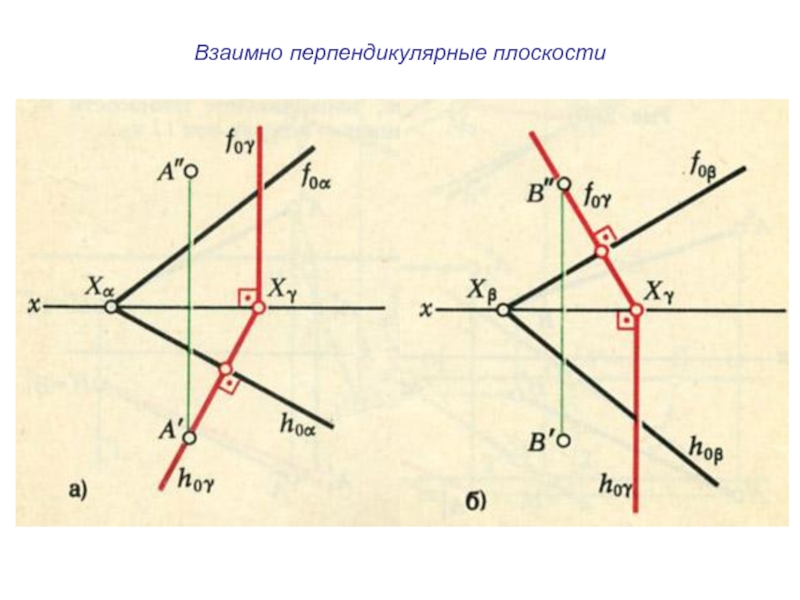
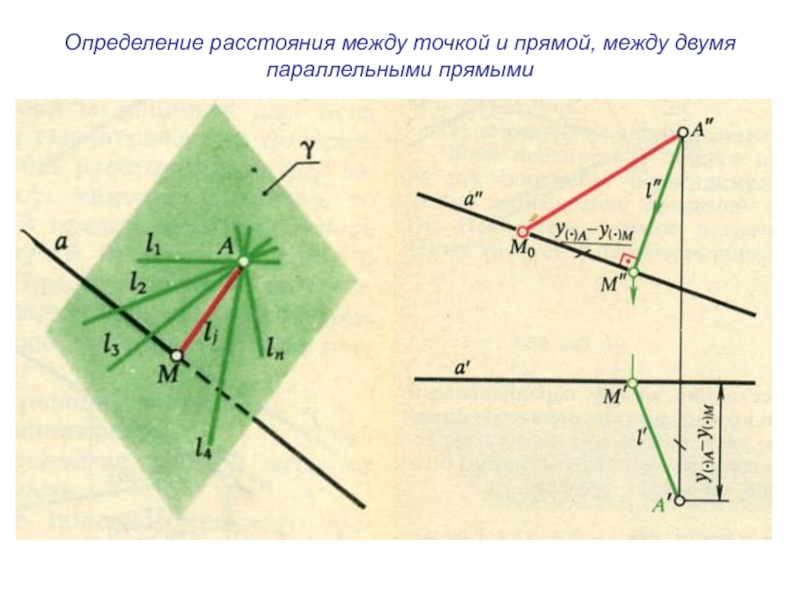
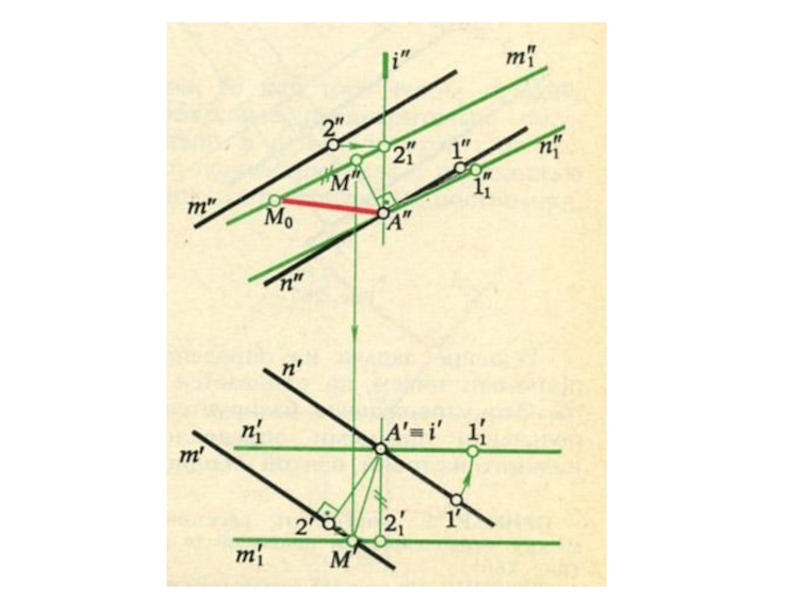
3. Аксонометрические проекцииТеорема Польке. Три отрезка произвольной длины,
4. Слайд 4
5. Слайд 5
6. Слайд 6
7. Слайд 7
8. Слайд 8
9. Слайд 9
10. Слайд 10
11. Слайд 11
12. Слайд 12
13. Слайд 13
14. Слайд 14
15. Слайд 15
16. Слайд 16
17. Слайд 17
18. Метрические задачи - задачи на
19. Взаимно перпендикулярные прямые
20. Слайд 20
21. Взаимно перпендикулярные прямая и плоскость
22. Слайд 22
23. Слайд 23
24. Взаимно перпендикулярные плоскости
25. Взаимно перпендикулярные плоскости
26. Определение расстояния между точкой и прямой, между двумя параллельными прямыми
27. Слайд 27
28. Определение расстояния между точкой и плоскостью, прямой и плоскостью, между плоскостями и скрещивающимися прямыми
29. Определение расстояния между точкой и плоскостью:расстояние от
30. Определение расстояния между плоскостями:расстояние между плоскостями определяется
31. Определение расстояния между скрещивающимися прямыми:расстояние между скрещивающимися
32. Проекции плоских угловЕсли стороны угла не параллельны
33. Определение величины плоского угла по его ортогональным проекциям
34. Определение угла между прямой и плоскостью
35. Определение угла между плоскостямимерой угла между двумя
36. Слайд 36
37. Слайд 37
38. Определение угла между скрещивающимися прямымиугол между скрещивающимися
39. Позиционные задачизадачи на принадлежность:принадлежность точки линии,принадлежность точки
40. Принадлежность точки линии
41. Принадлежность точки поверхности
42. Принадлежность точки поверхности
43. Принадлежность точки поверхности
44. Принадлежность точки поверхности
45. Принадлежность точки поверхности
46. Принадлежность линии поверхности
47. Пересечение линии с линией
48. Пересечение плоскостей
49. Пересечение плоскостей
50. Пересечение плоскостей
51. Слайд 51
52. Слайд 52
53. Слайд 53
54. Слайд 54
55. Слайд 55
56. Слайд 56
57. Слайд 57
58. Слайд 58
59. Слайд 59
60. Слайд 60
61. Слайд 61
62. Слайд 62
63. Слайд 63
64. Слайд 64
65. Слайд 65
66. Слайд 66
67. Слайд 67
68. Слайд 68
69. Слайд 69
70. Слайд 70
71. Слайд 71
72. Слайд 72
73. Слайд 73
74. Слайд 74
75. Слайд 75
76. Слайд 76
77. Слайд 77
78. Слайд 78
79. Слайд 79
80. Слайд 80
81. Слайд 81
82. Слайд 82
83. Слайд 83
84. Слайд 84
85. Скачать презентанцию

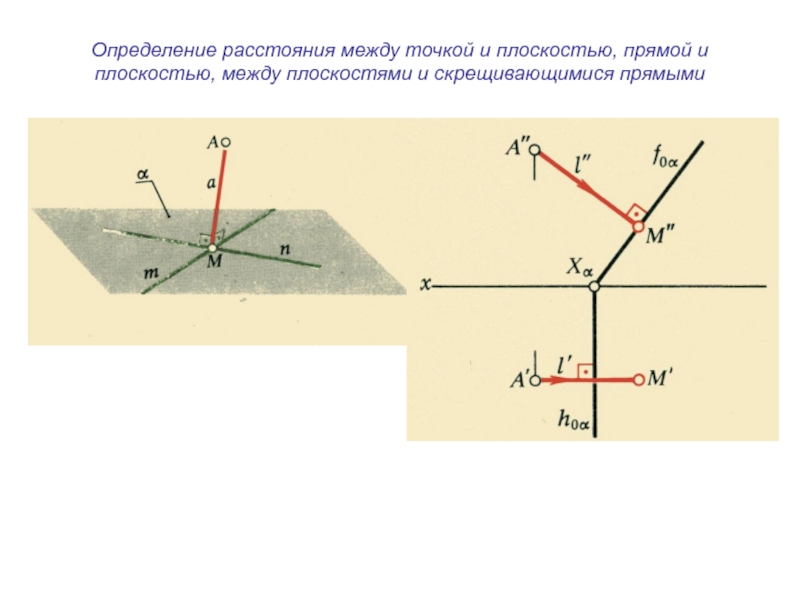
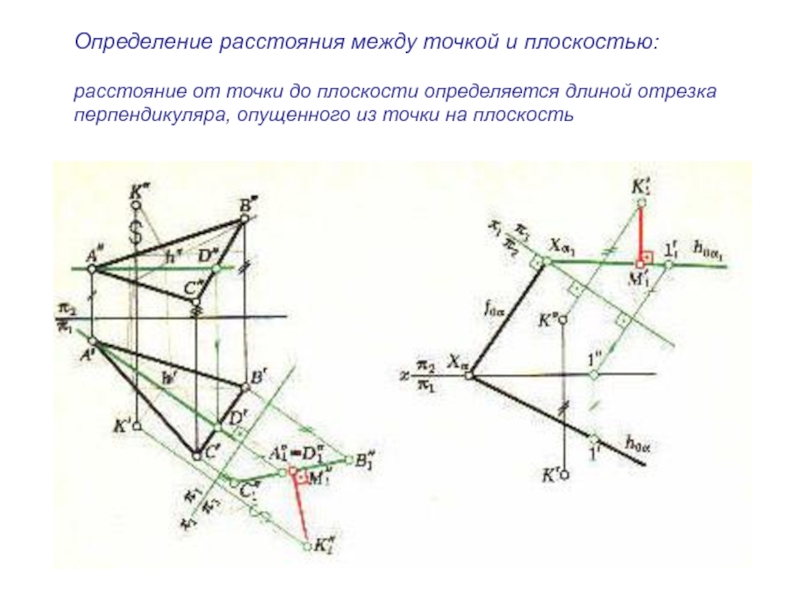
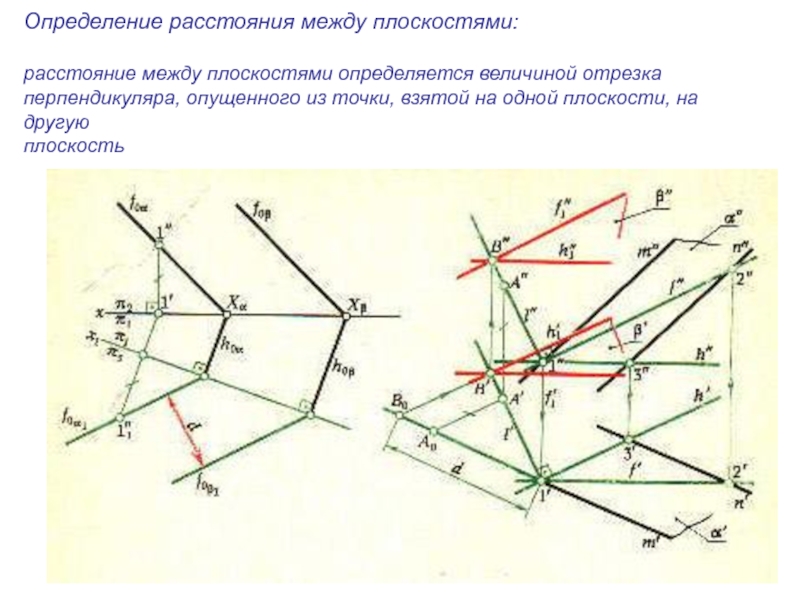
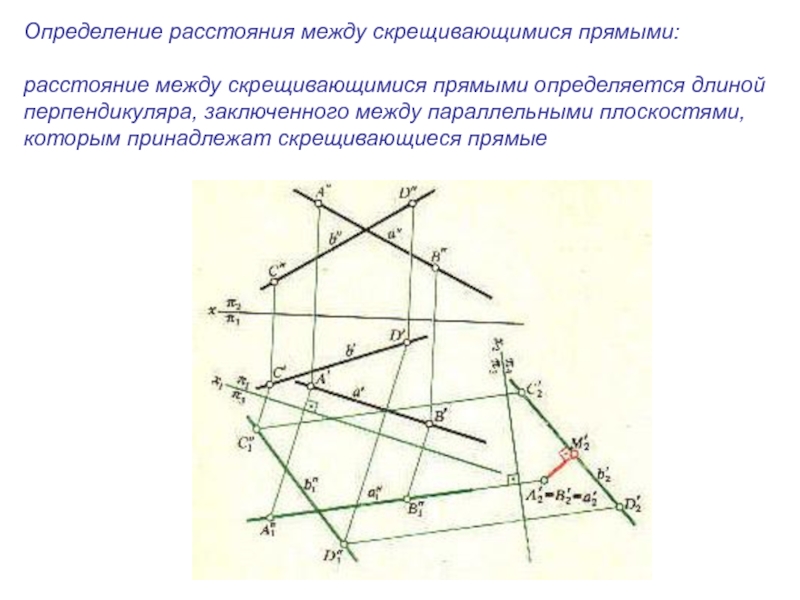
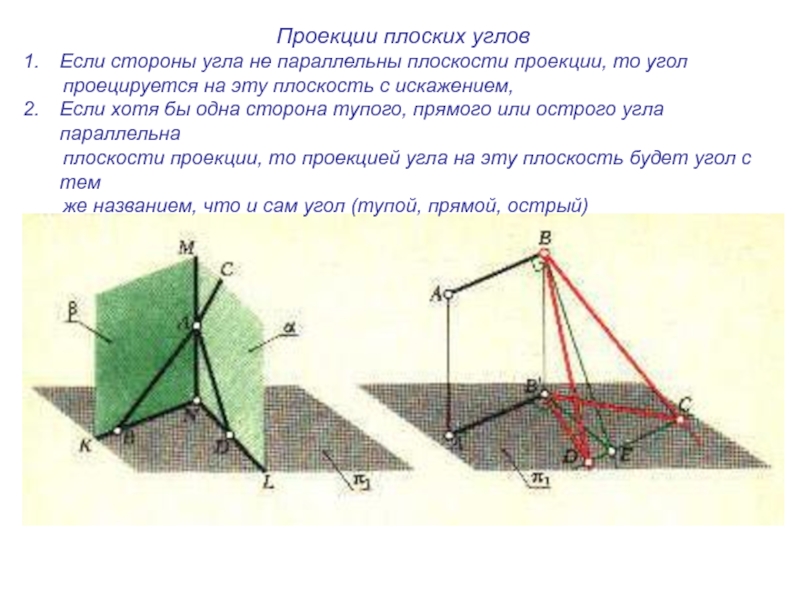
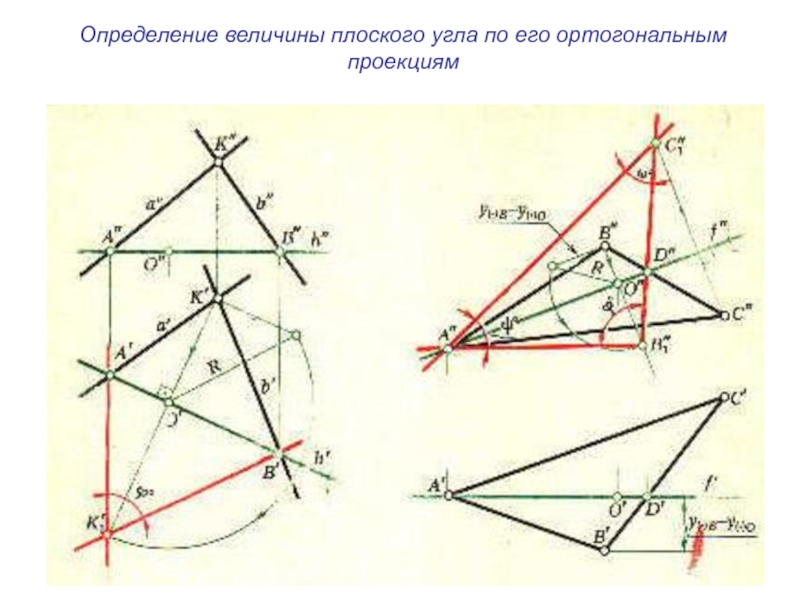
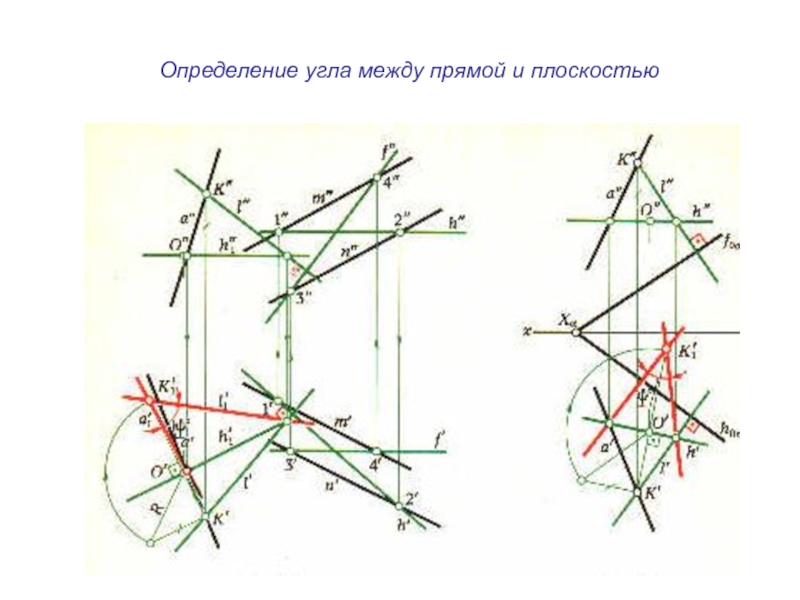
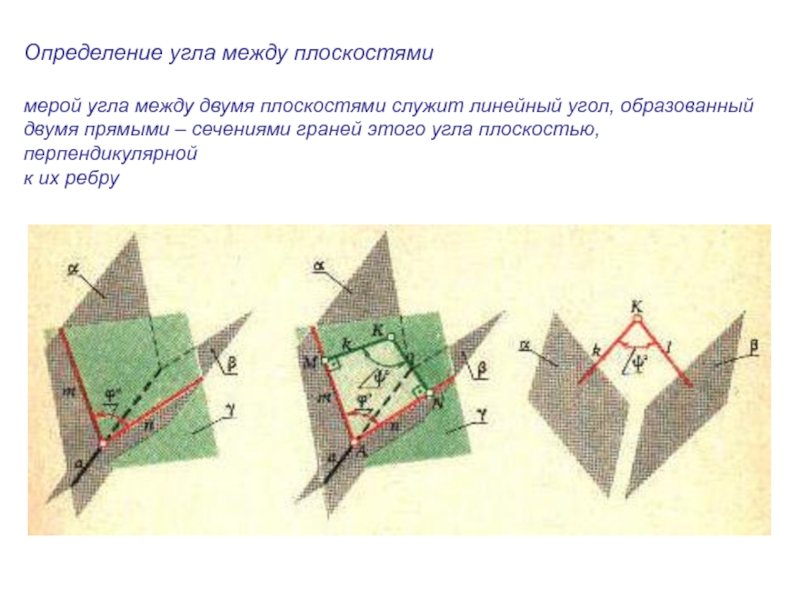
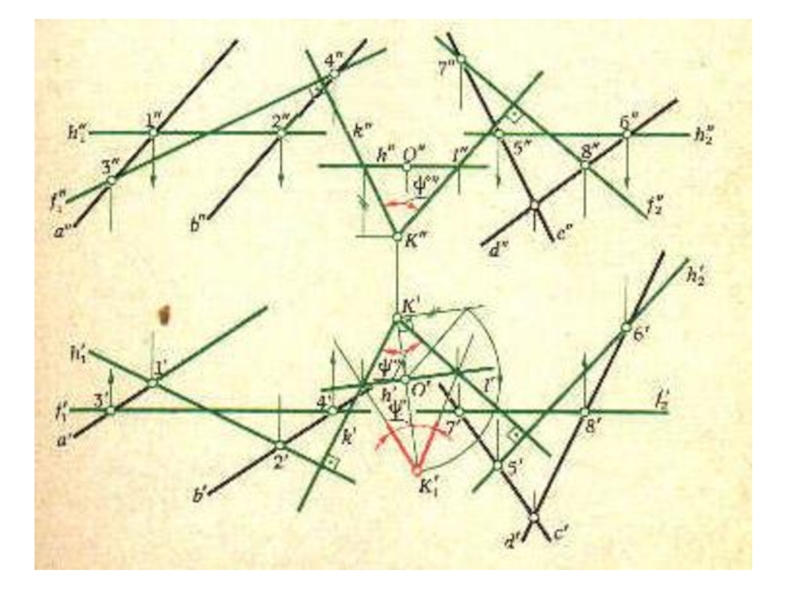
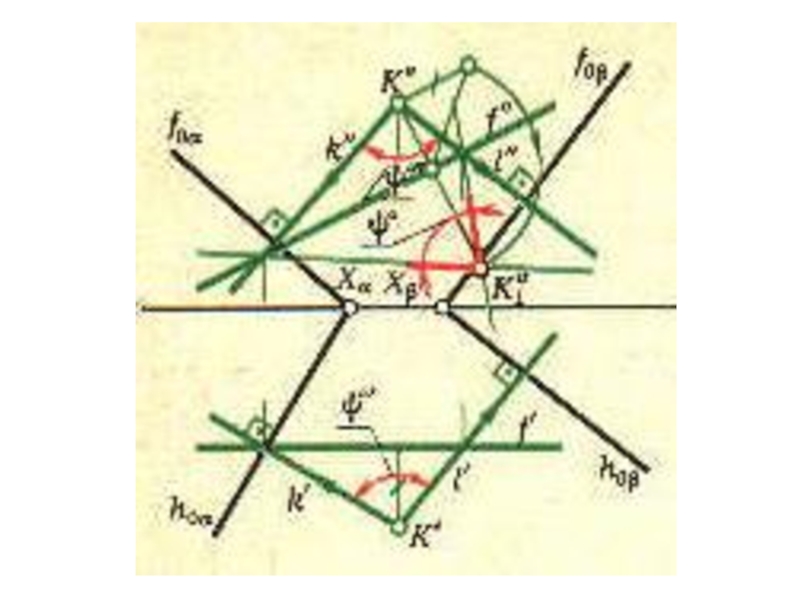
Аксонометрические проекции

Главная
Разное
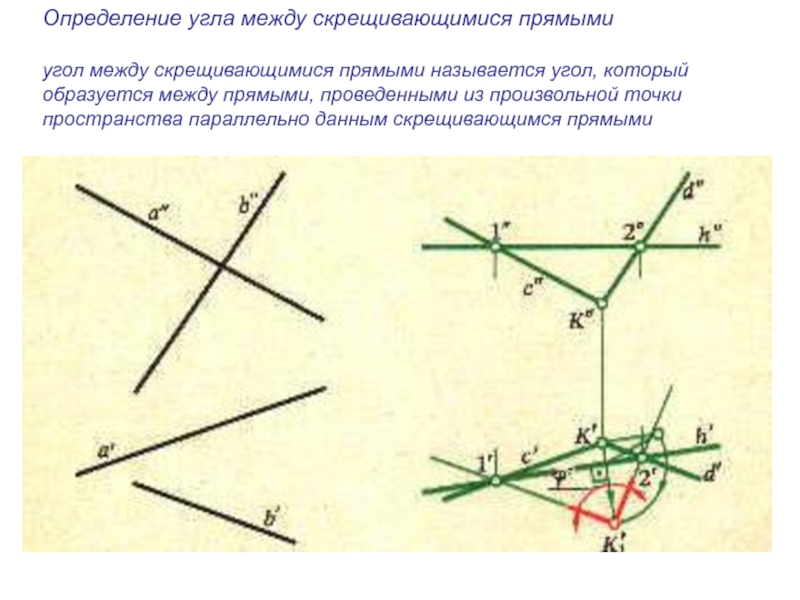
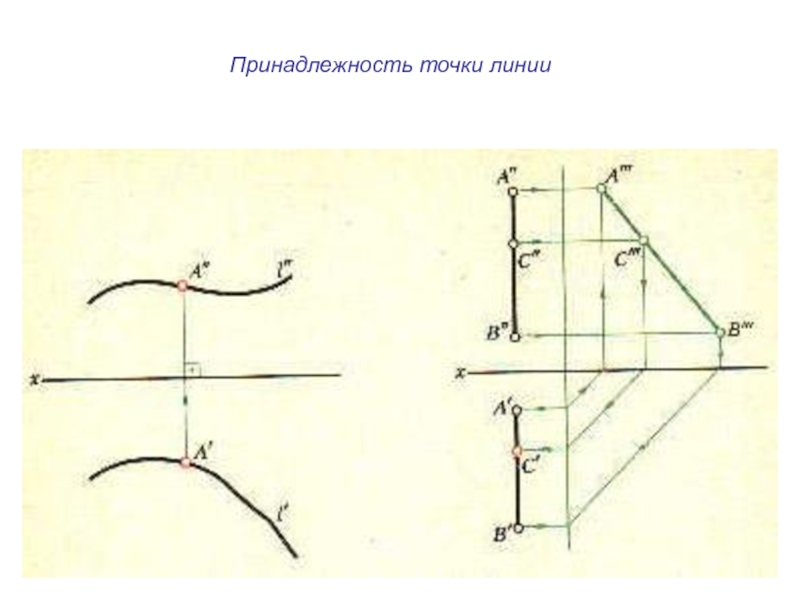
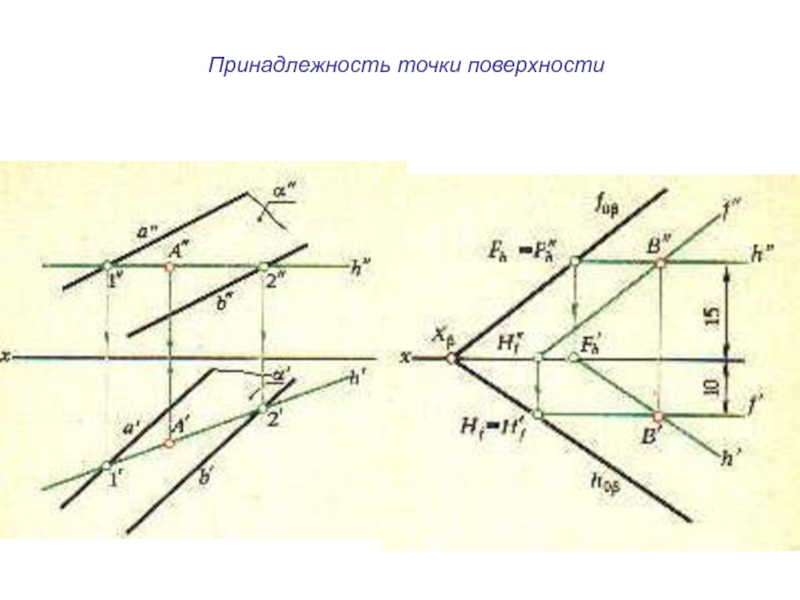
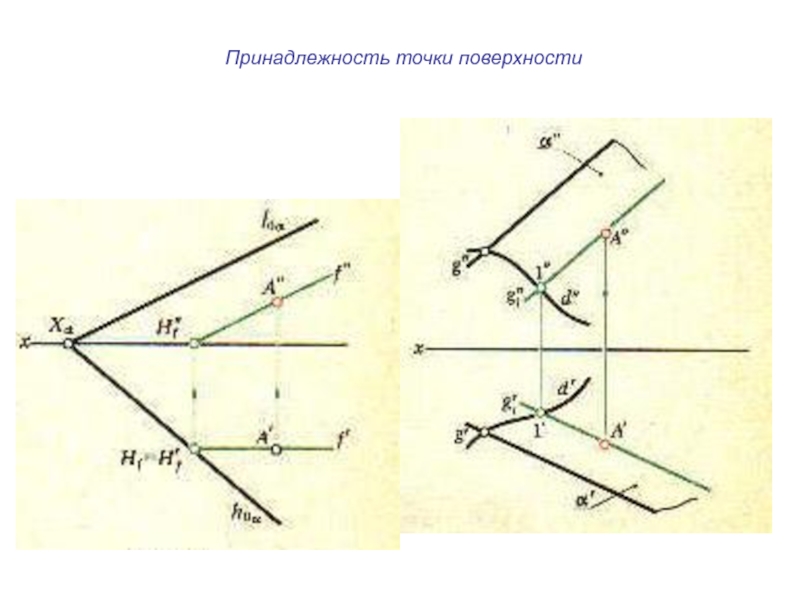
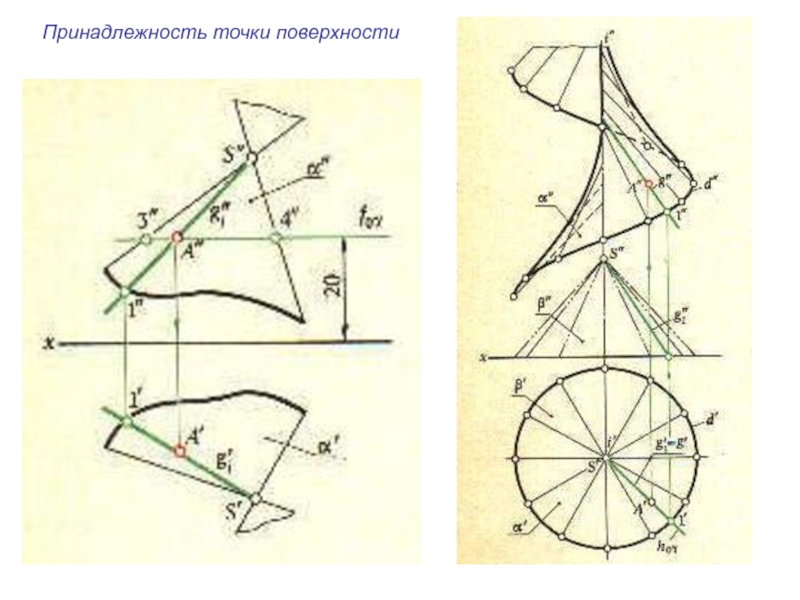
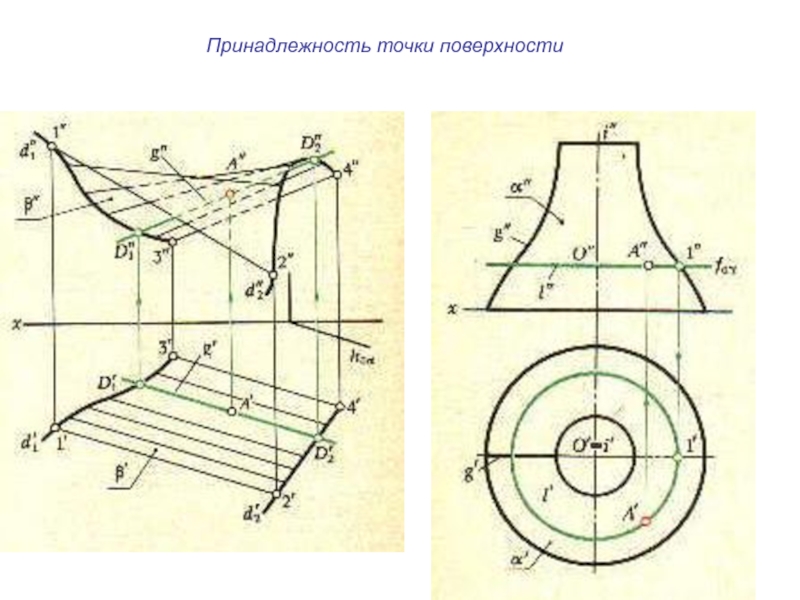
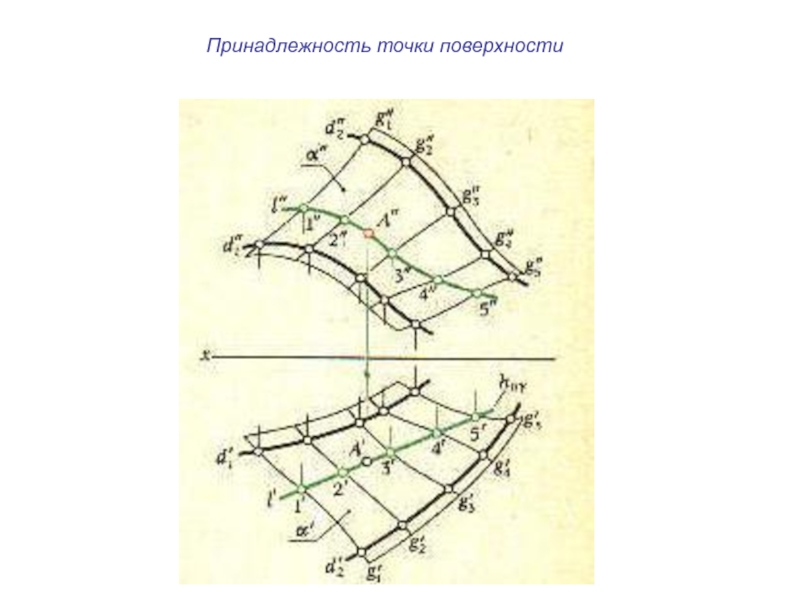
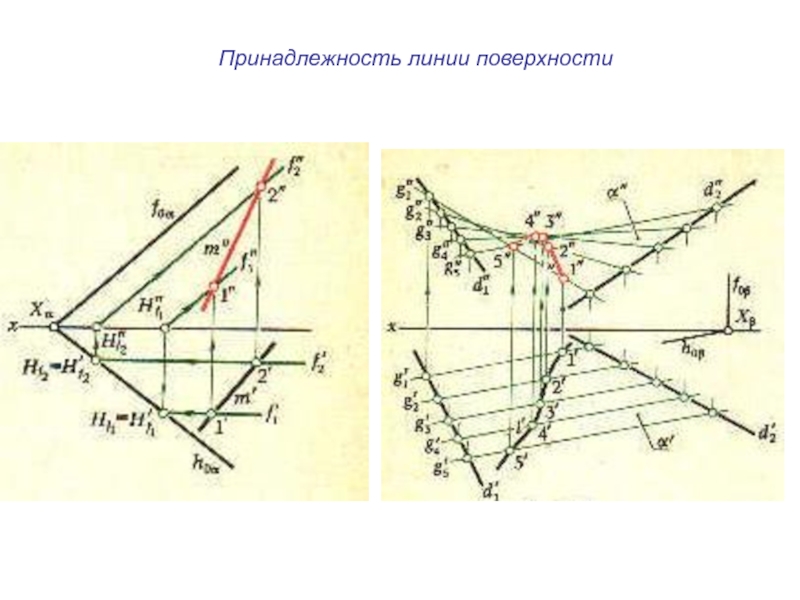
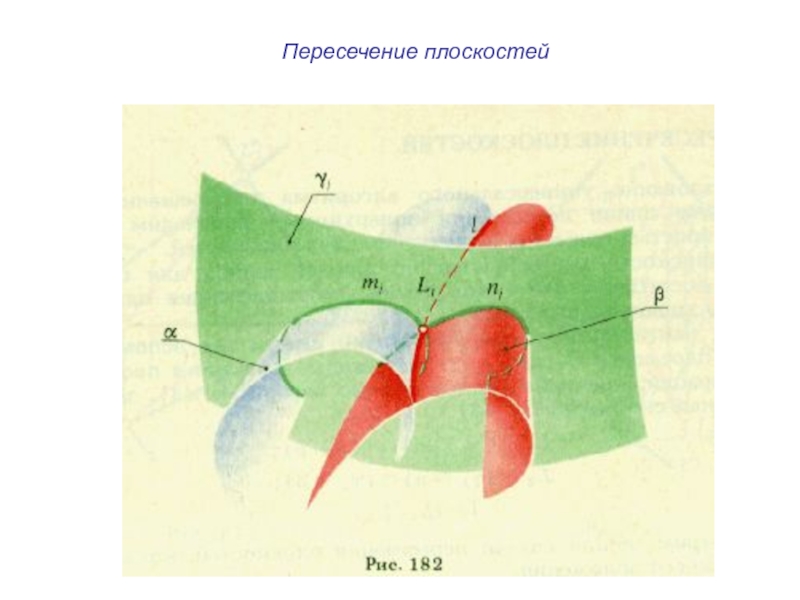
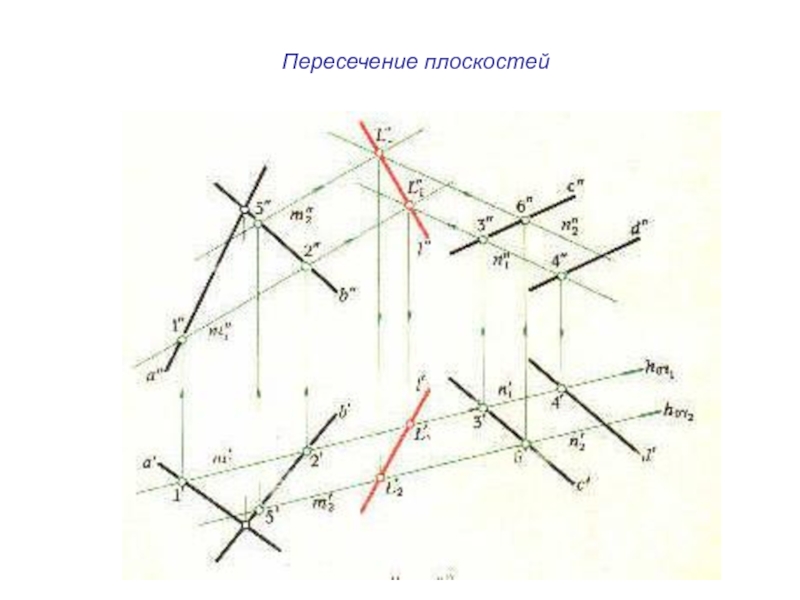
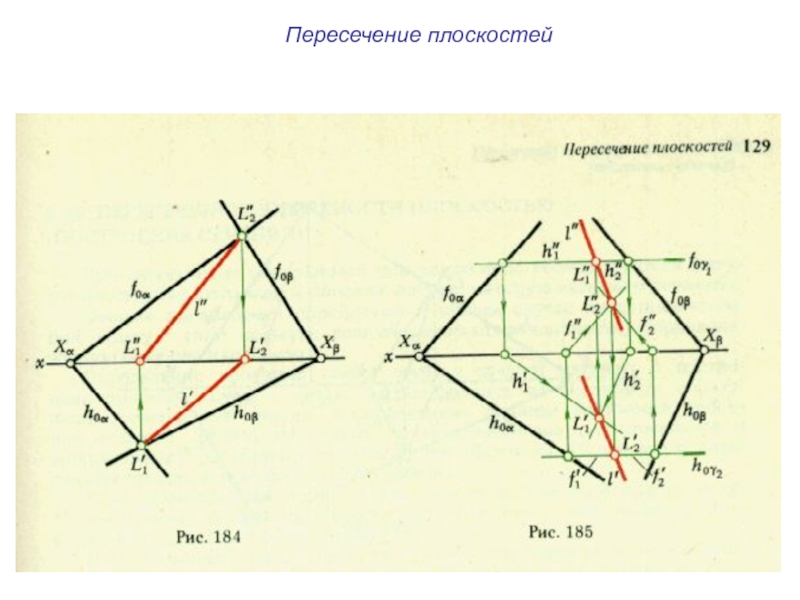
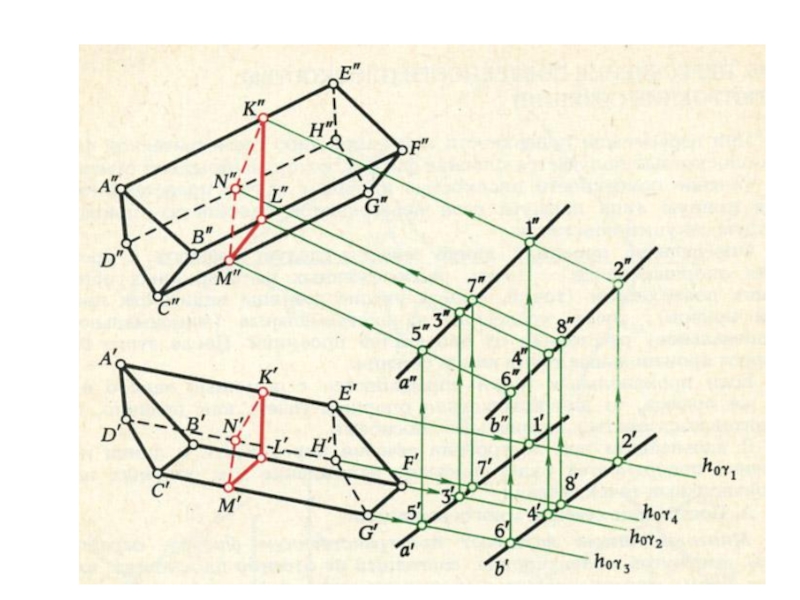
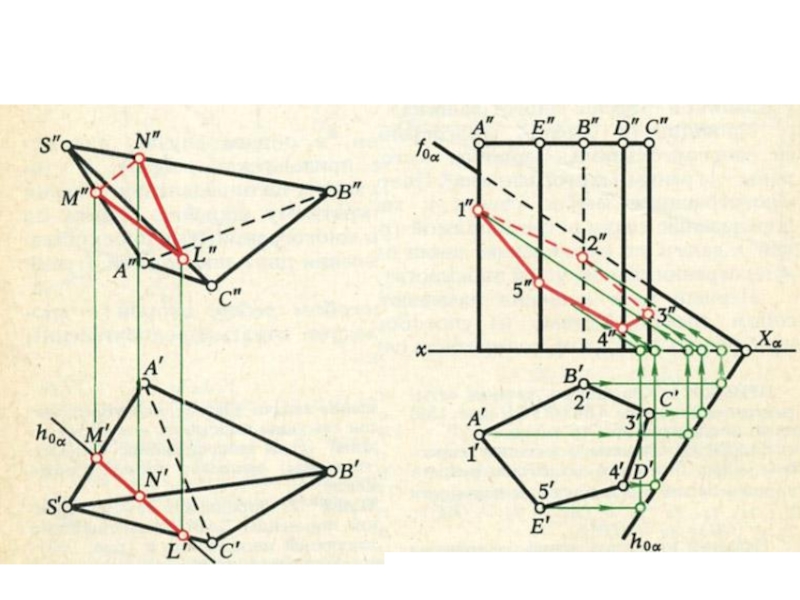
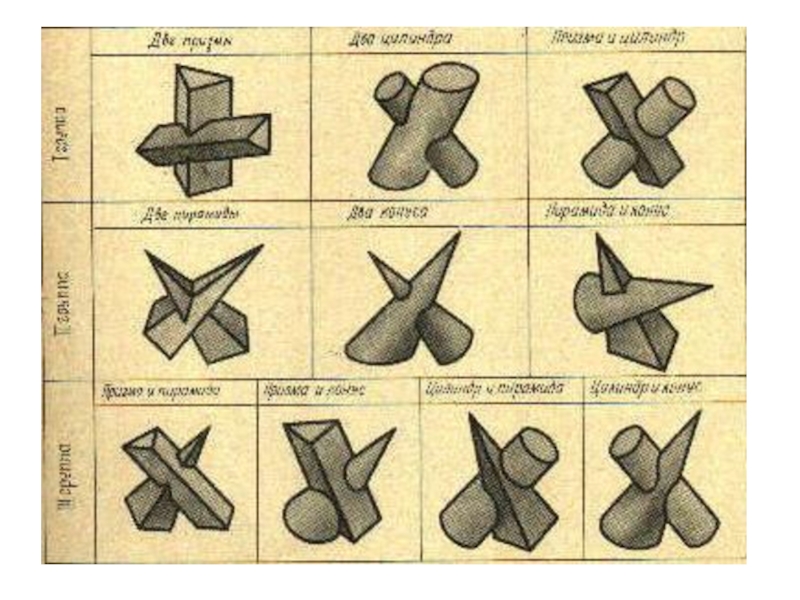
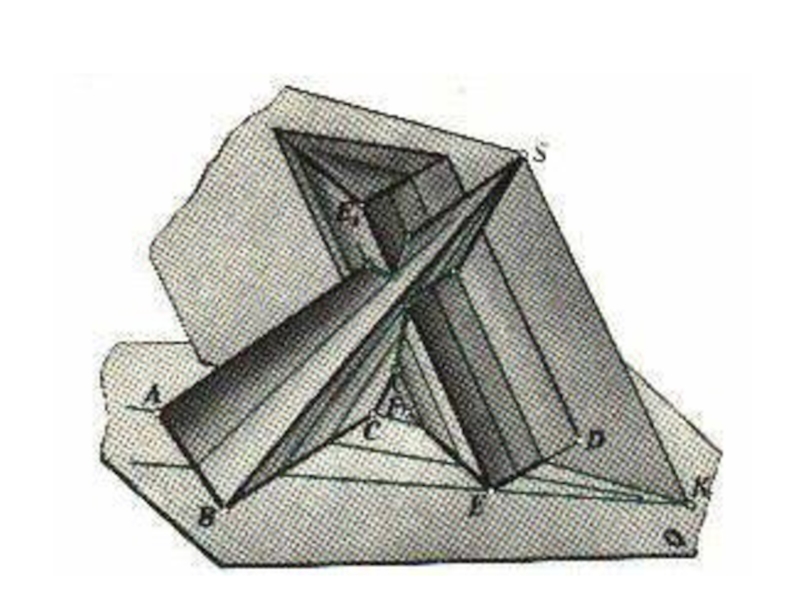
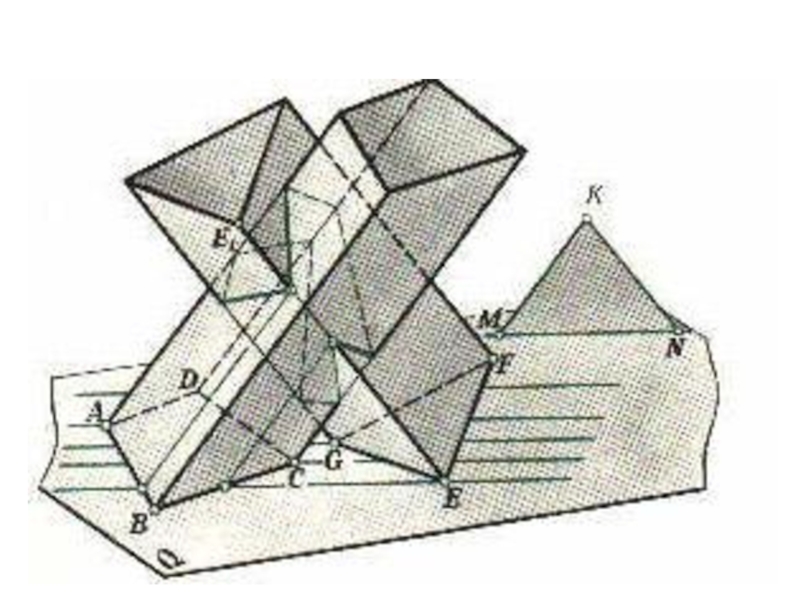
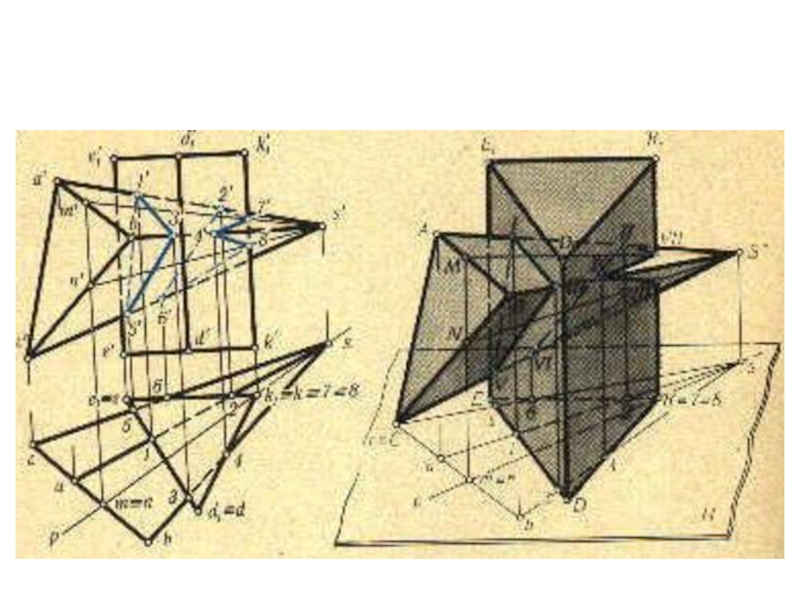
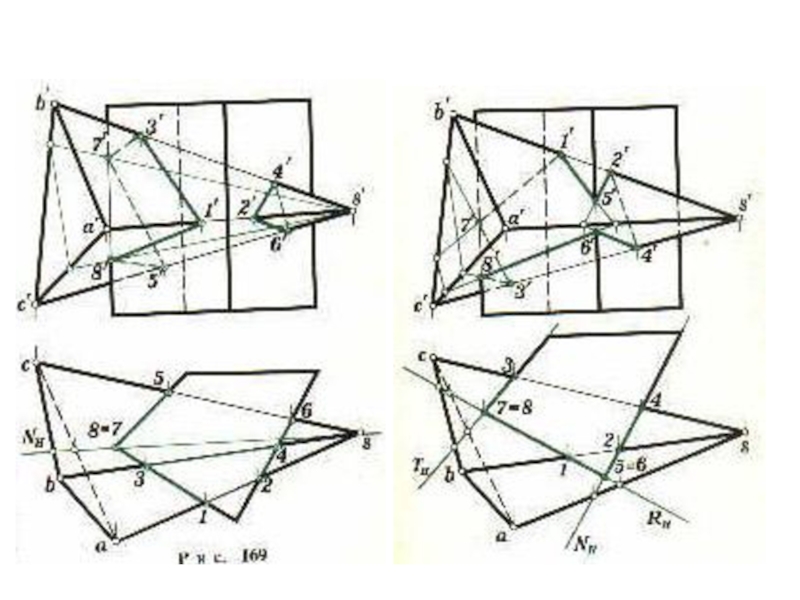
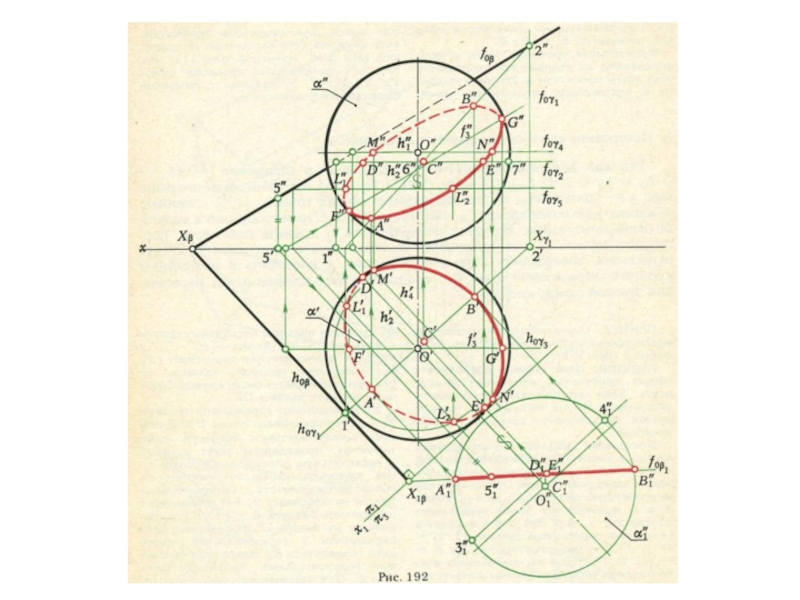
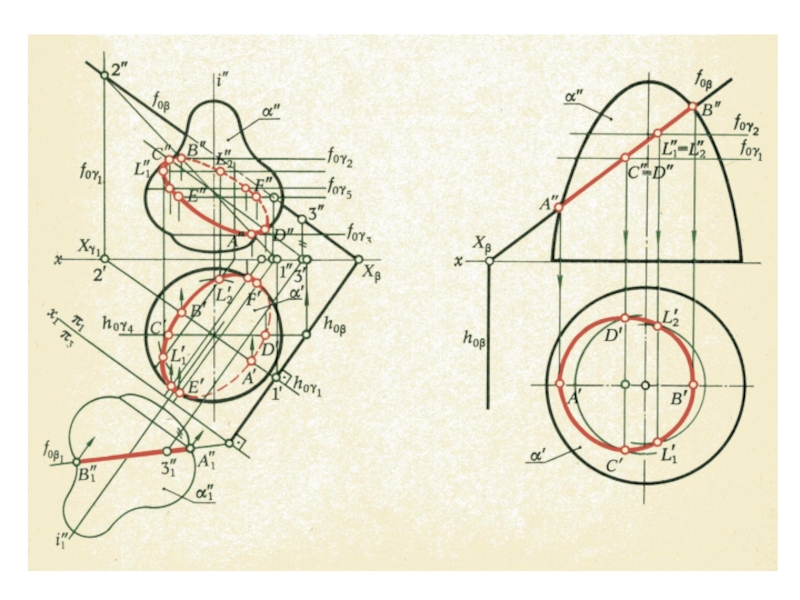
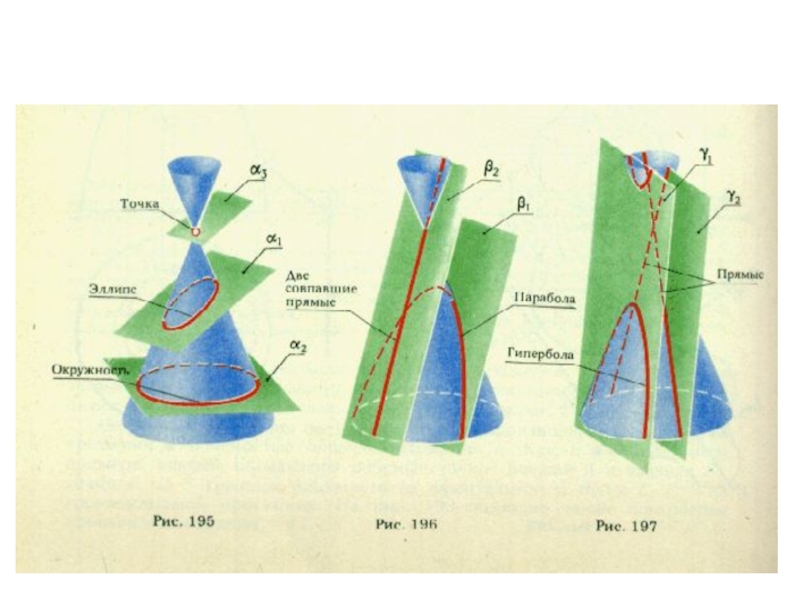
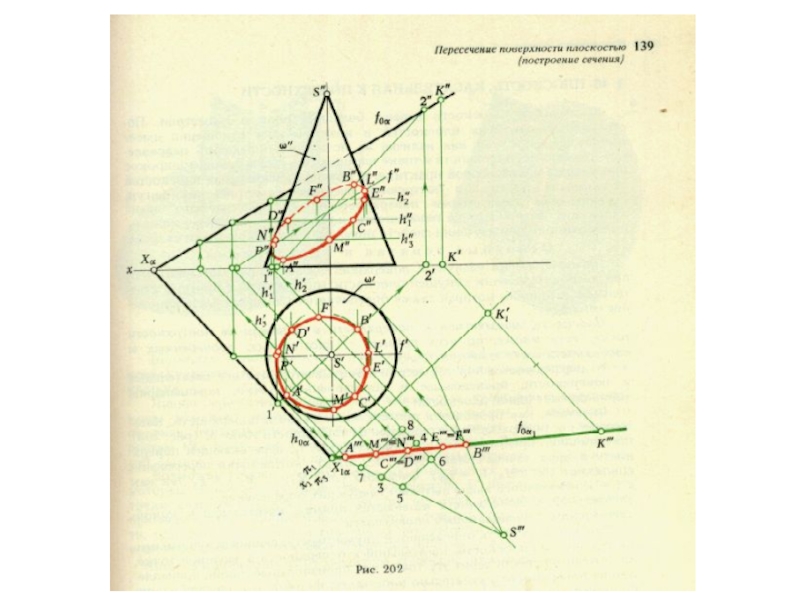
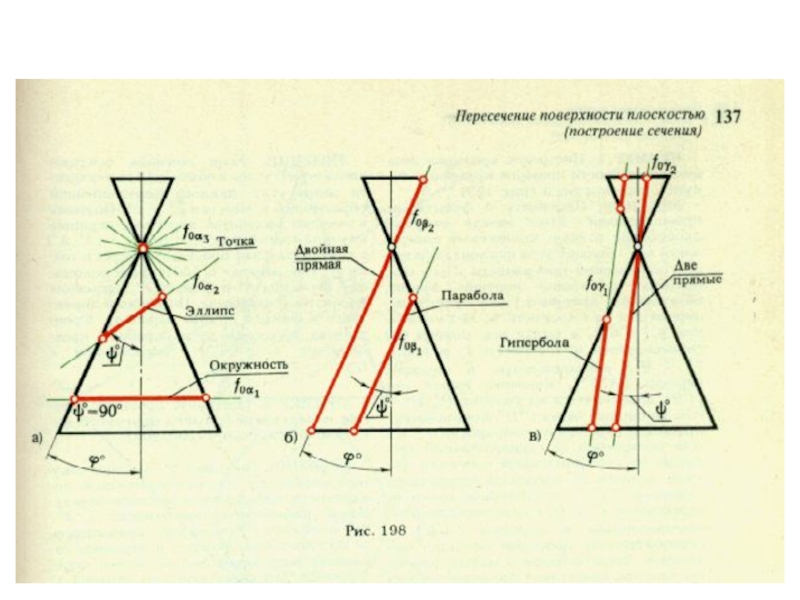
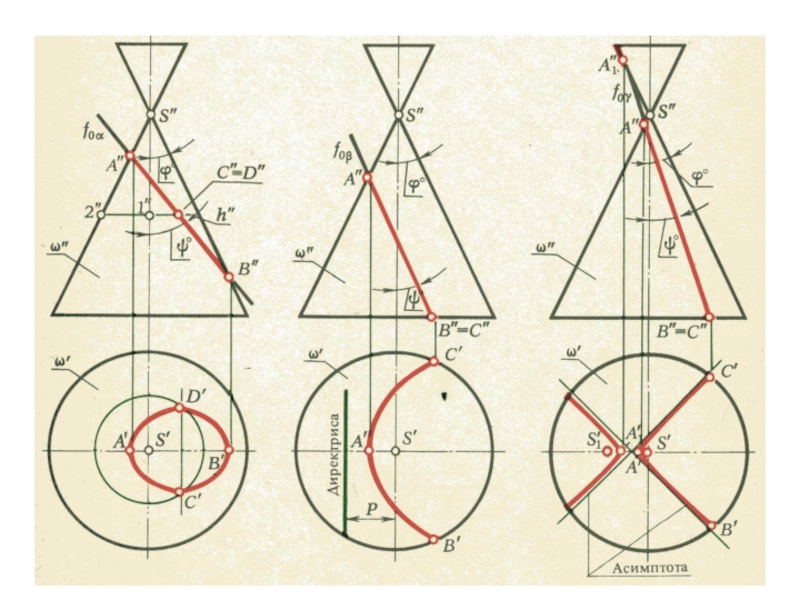
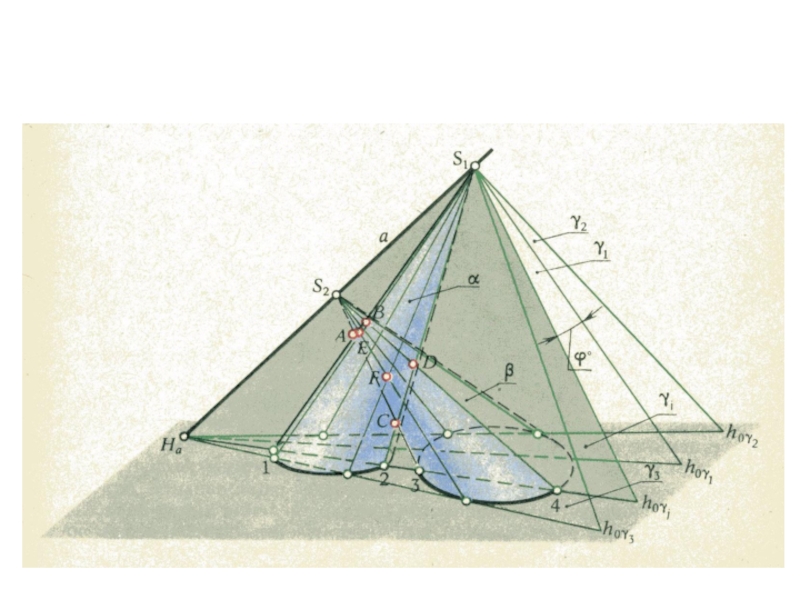
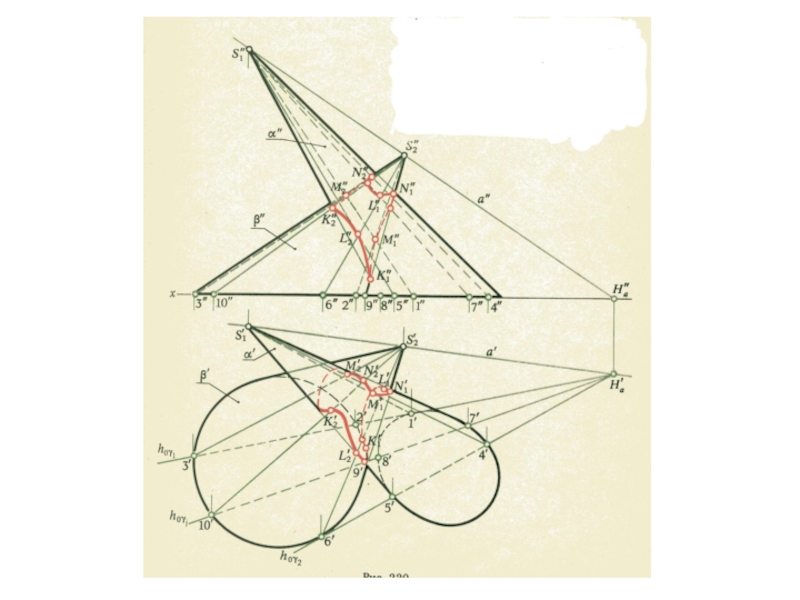
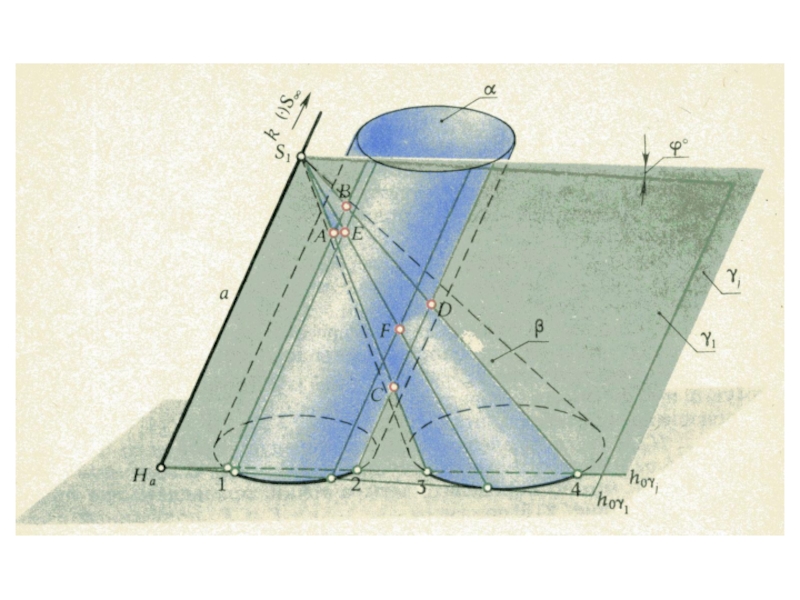
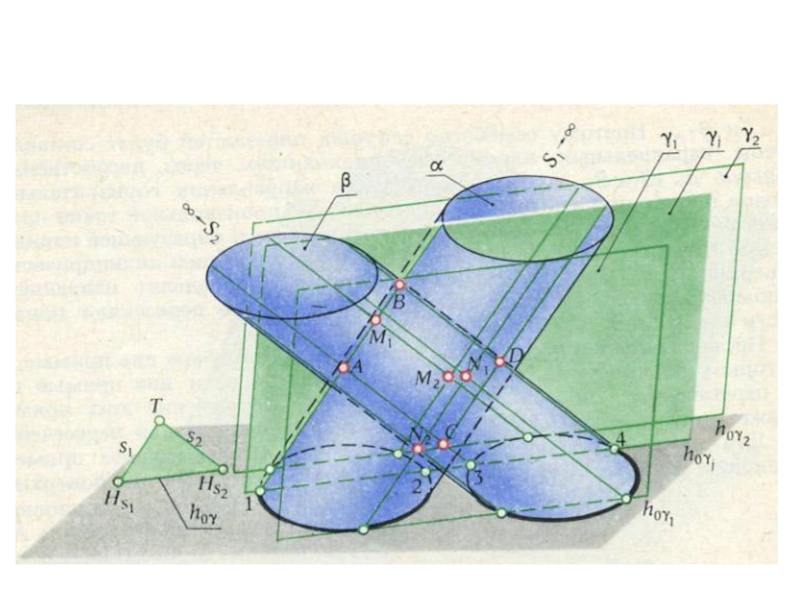
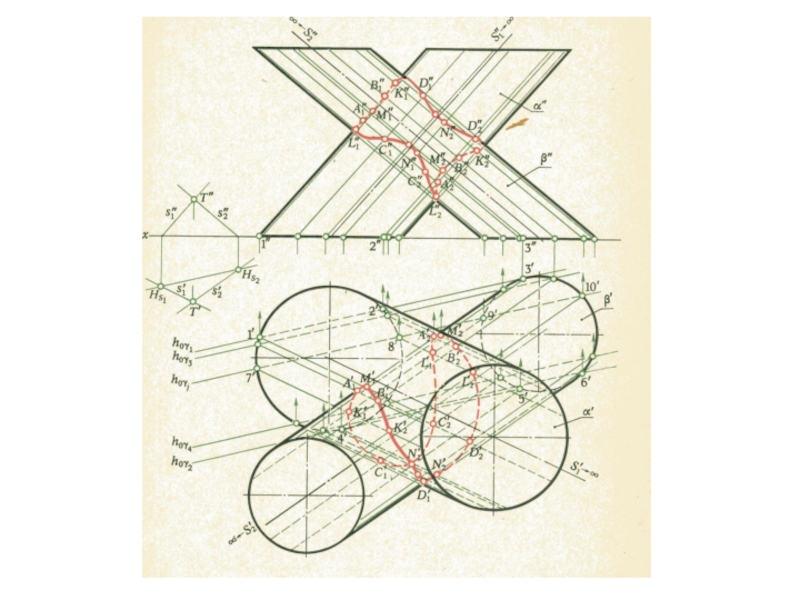
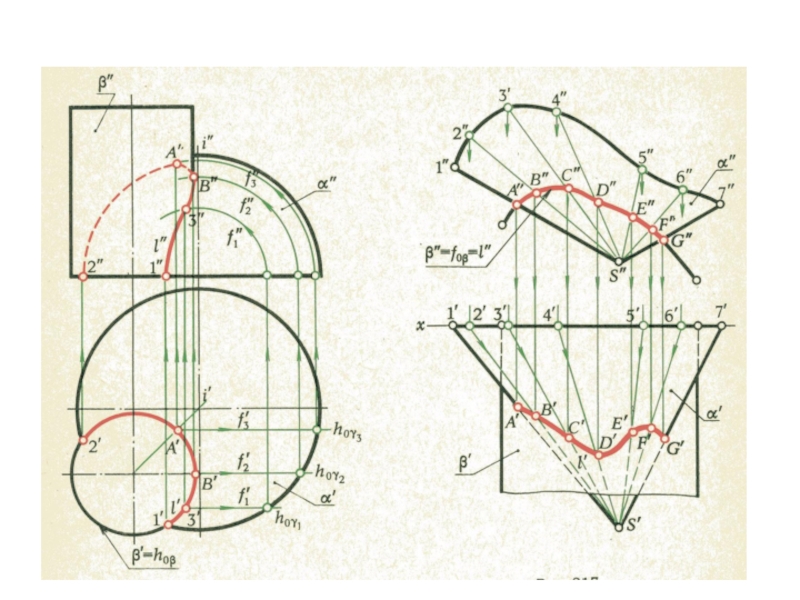
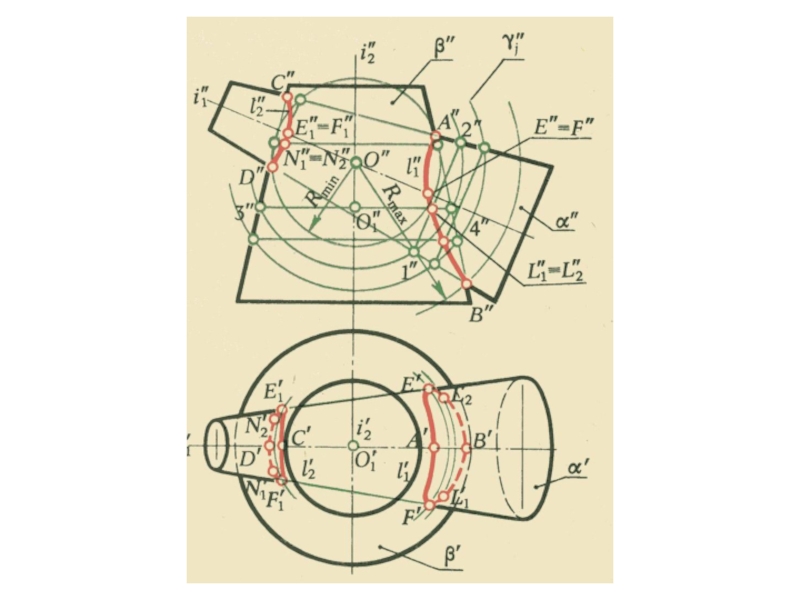
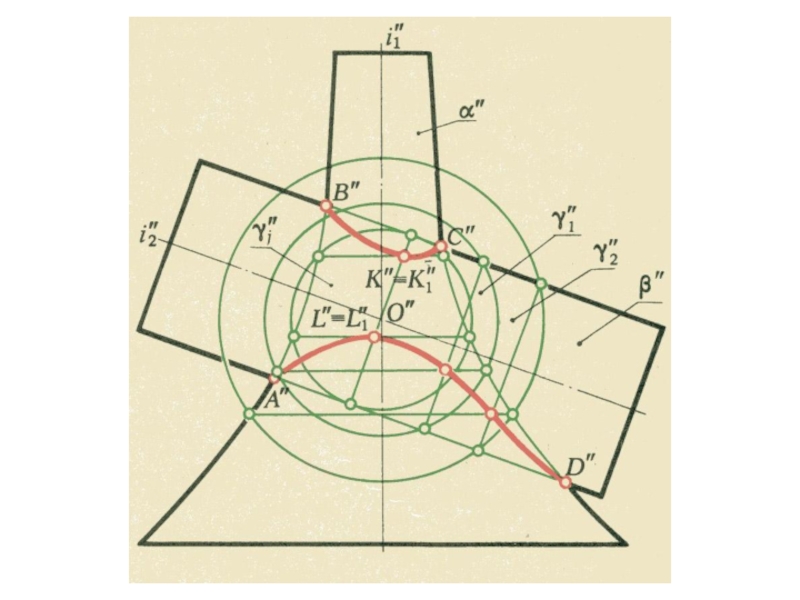
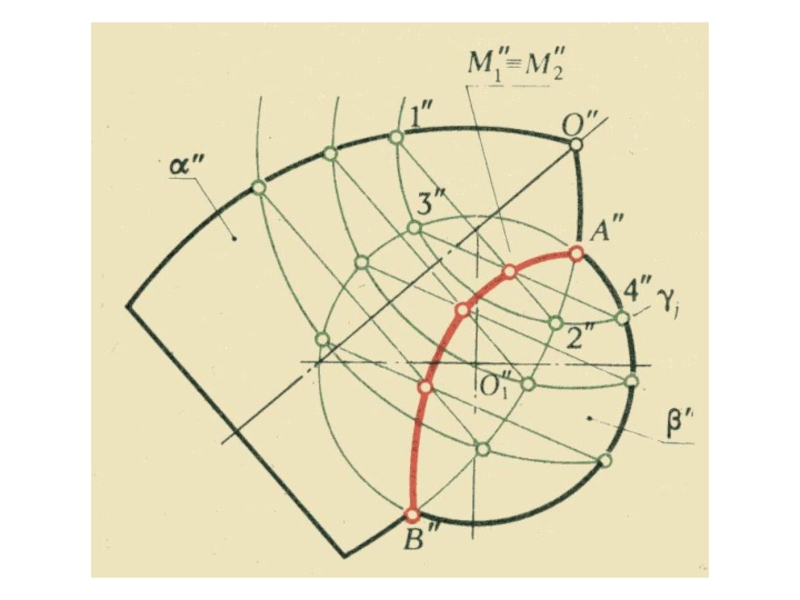
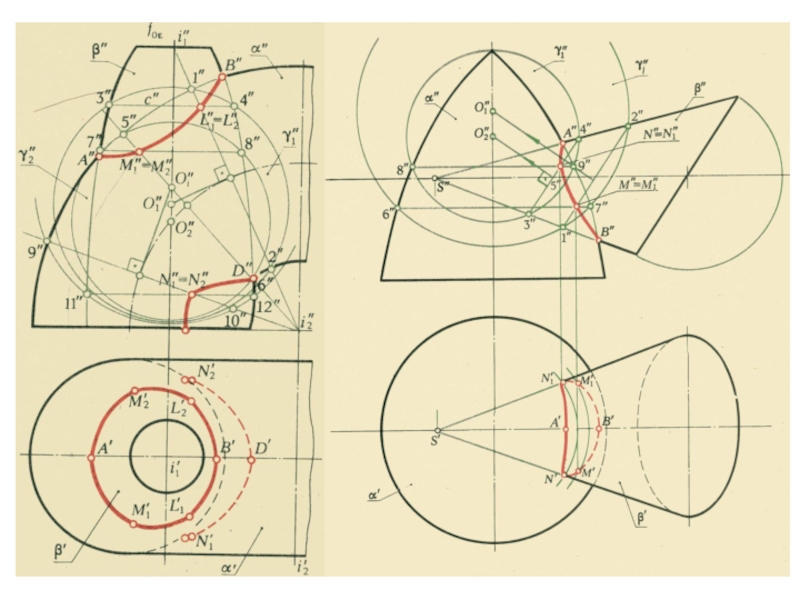
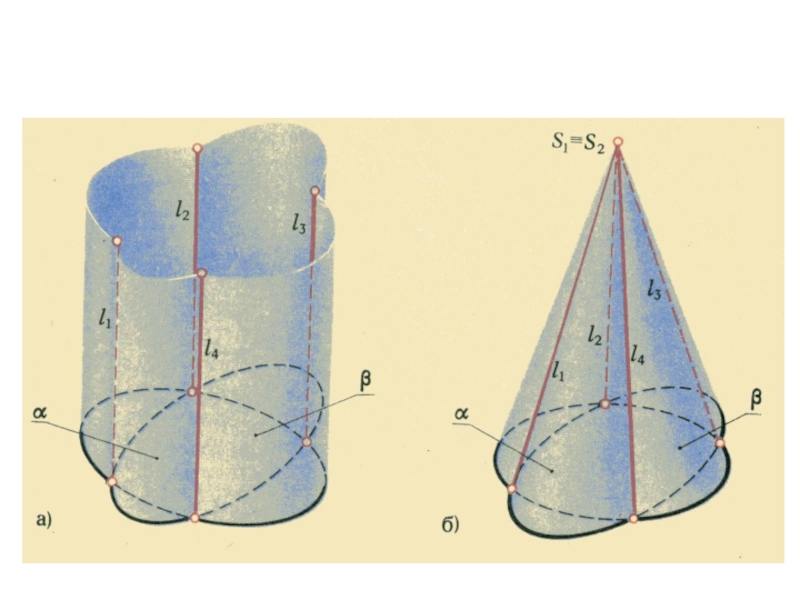
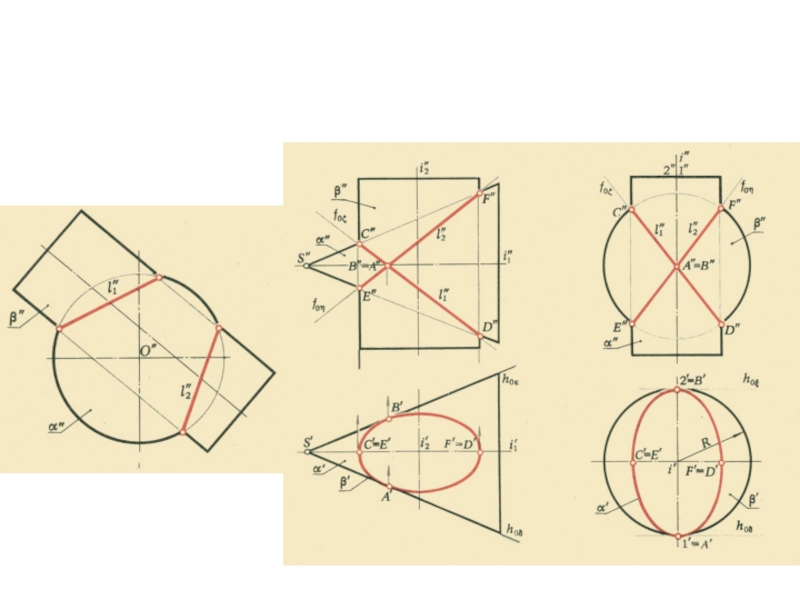
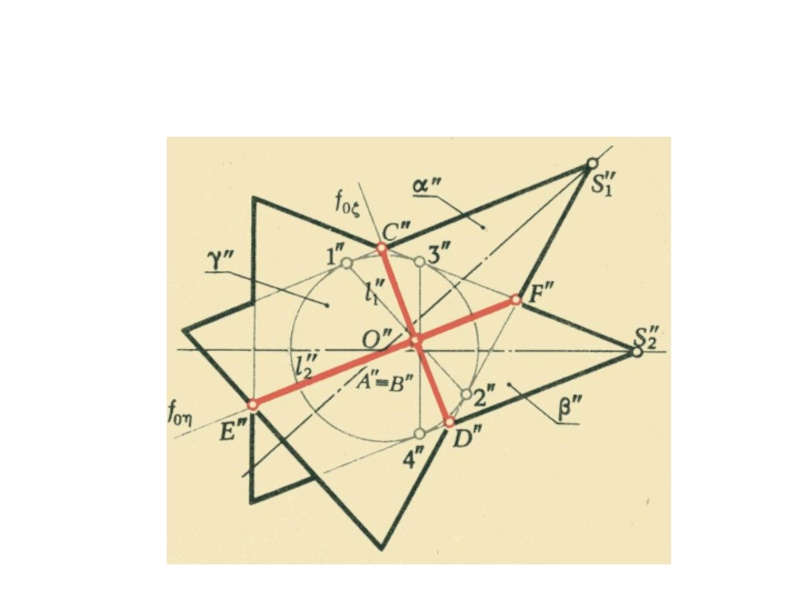
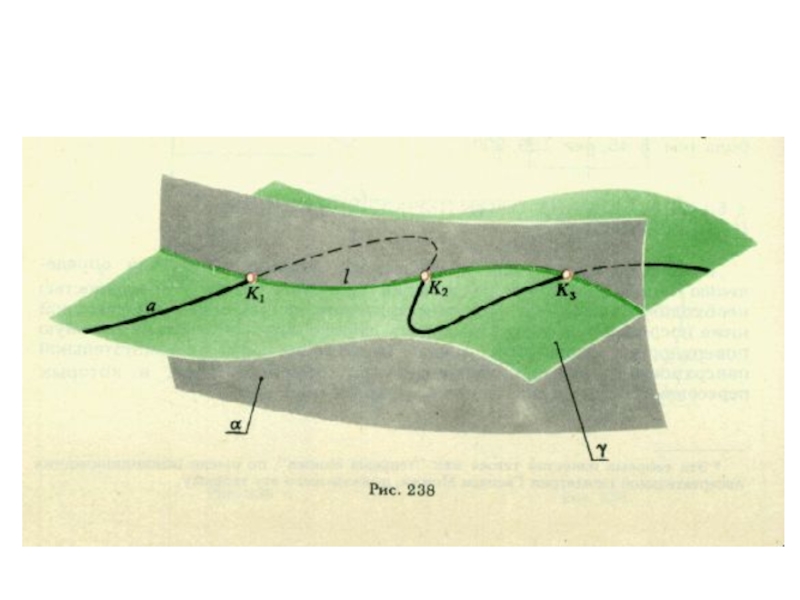
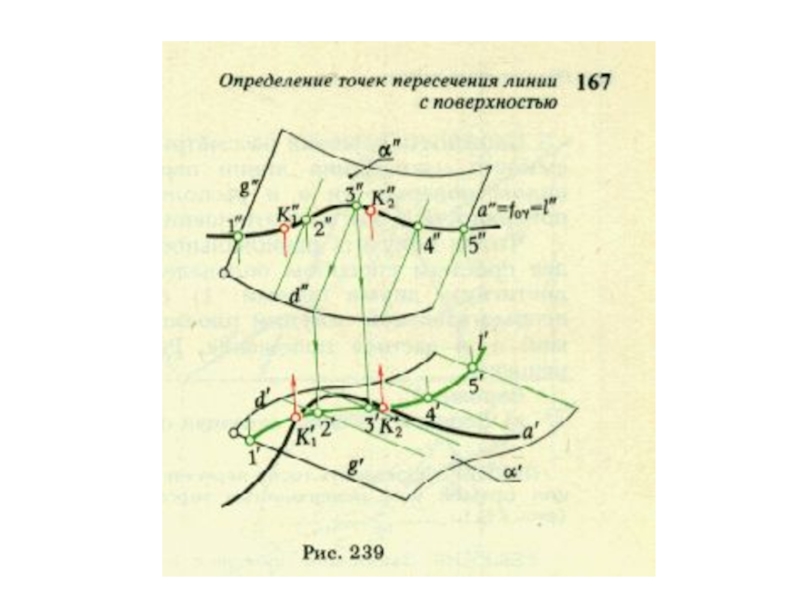
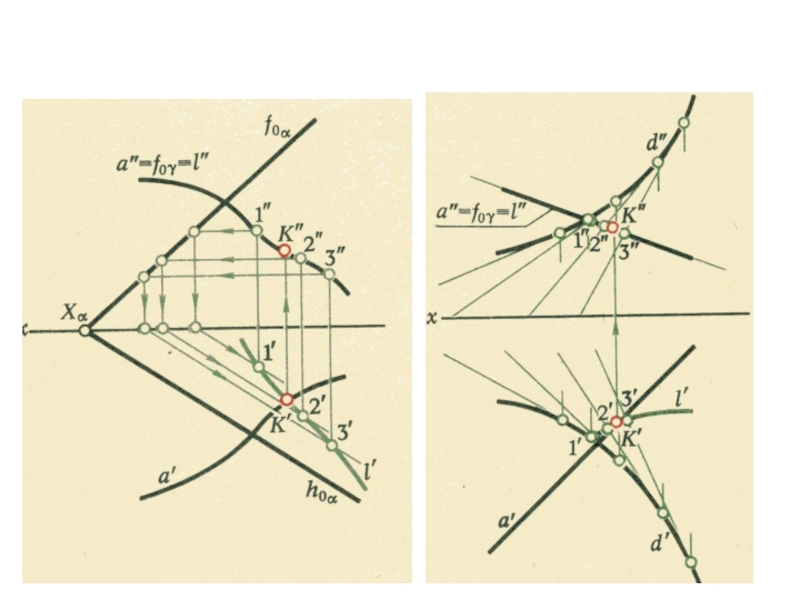
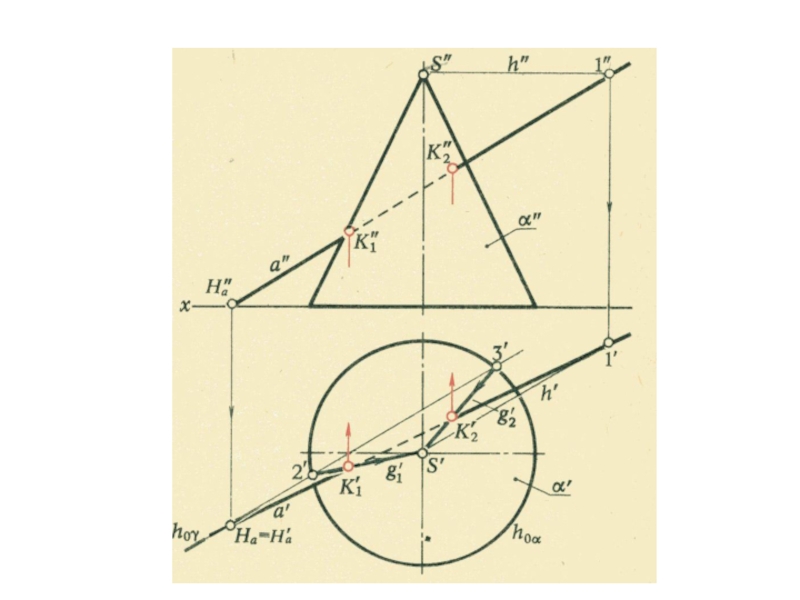
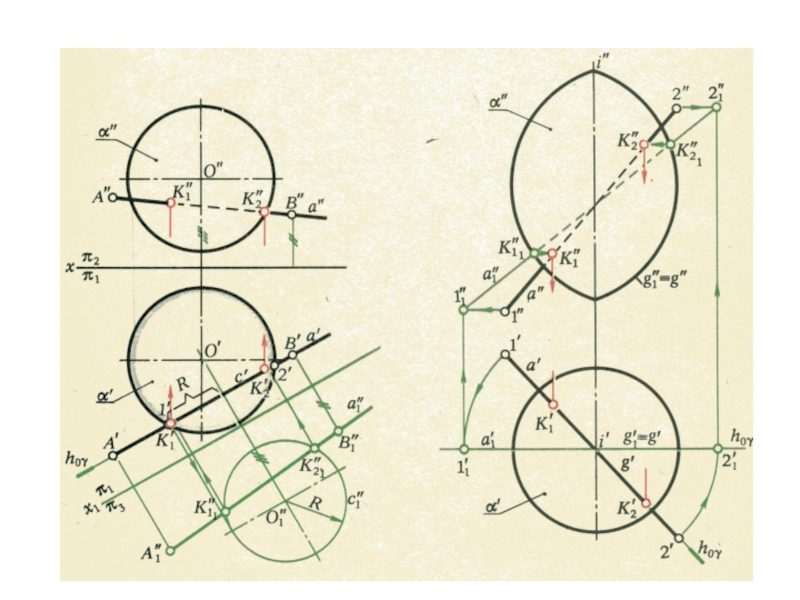
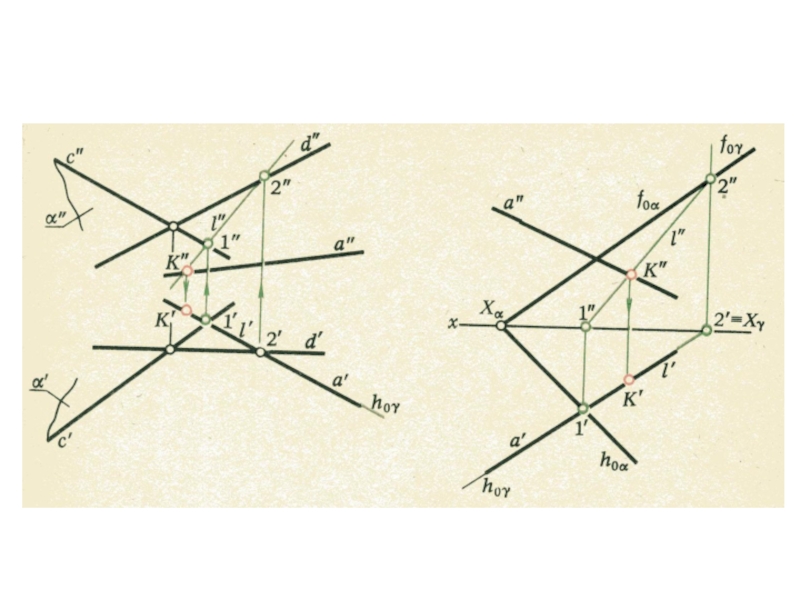
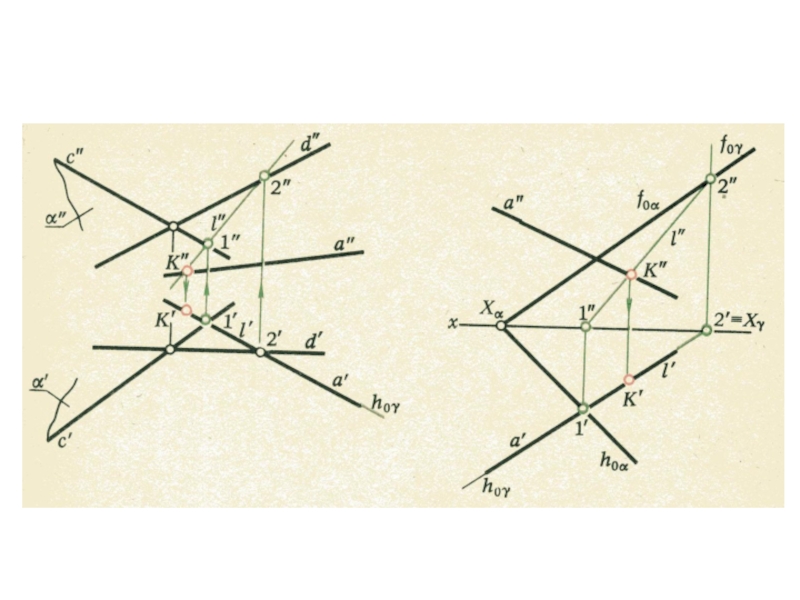
Аксонометрические проекции

Слайды и текст этой презентации

Слайд 1Аксонометрические проекции

Аксонометрические проекции

Слайд 2Аксонометрические проекции

Аксонометрические проекции

Слайд 3Аксонометрические проекции
Теорема Польке. Три отрезка произвольной длины, лежащие в одной

плоскости и
выходящие из одной точки под произвольными углами друг

к другу – представляют
собой параллельные проекции трех равных отрезков, отложенных на
прямоугольных осях координат от начала.

Аксонометрические проекцииТеорема Польке. Три отрезка произвольной длины, лежащие в одной плоскости и выходящие из одной точки под

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18Метрические задачи - задачи на определение расстояния

между двумя точками; - задачи на нахождение величины

угла между двумя пересекающими прямыми.

Метрические задачи - задачи на определение расстояния между двумя точками;

Слайд 19Взаимно перпендикулярные прямые

Взаимно перпендикулярные прямые

Слайд 20

Слайд 21Взаимно перпендикулярные прямая и плоскость

Взаимно перпендикулярные прямая и плоскость

Слайд 22

Слайд 23

Слайд 24Взаимно перпендикулярные плоскости

Взаимно перпендикулярные плоскости

Слайд 25Взаимно перпендикулярные плоскости

Взаимно перпендикулярные плоскости

Слайд 26Определение расстояния между точкой и прямой, между двумя параллельными прямыми

Определение расстояния между точкой и прямой, между двумя параллельными прямыми

Слайд 27

Слайд 28Определение расстояния между точкой и плоскостью, прямой и плоскостью, между

плоскостями и скрещивающимися прямыми

Определение расстояния между точкой и плоскостью, прямой и плоскостью, между плоскостями и скрещивающимися прямыми

Слайд 29Определение расстояния между точкой и плоскостью:

расстояние от точки до плоскости

определяется длиной отрезка
перпендикуляра, опущенного из точки на плоскость

Определение расстояния между точкой и плоскостью:расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки

Слайд 30Определение расстояния между плоскостями:

расстояние между плоскостями определяется величиной отрезка
перпендикуляра, опущенного

из точки, взятой на одной плоскости, на другую
плоскость

Определение расстояния между плоскостями:расстояние между плоскостями определяется величиной отрезкаперпендикуляра, опущенного из точки, взятой на одной плоскости, на

Слайд 31Определение расстояния между скрещивающимися прямыми:

расстояние между скрещивающимися прямыми определяется длиной
перпендикуляра,

заключенного между параллельными плоскостями,
которым принадлежат скрещивающиеся прямые

Определение расстояния между скрещивающимися прямыми:расстояние между скрещивающимися прямыми определяется длинойперпендикуляра, заключенного между параллельными плоскостями,которым принадлежат скрещивающиеся прямые

Слайд 32Проекции плоских углов
Если стороны угла не параллельны плоскости проекции, то

угол
проецируется на эту плоскость с искажением,
Если хотя

бы одна сторона тупого, прямого или острого угла параллельна
плоскости проекции, то проекцией угла на эту плоскость будет угол с тем
же названием, что и сам угол (тупой, прямой, острый)

Проекции плоских угловЕсли стороны угла не параллельны плоскости проекции, то угол проецируется на эту плоскость

Слайд 33Определение величины плоского угла по его ортогональным проекциям

Определение величины плоского угла по его ортогональным проекциям

Слайд 34Определение угла между прямой и плоскостью

Определение угла между прямой и плоскостью

Слайд 35Определение угла между плоскостями

мерой угла между двумя плоскостями служит линейный

угол, образованный
двумя прямыми – сечениями граней этого угла плоскостью, перпендикулярной
к

их ребру

Определение угла между плоскостямимерой угла между двумя плоскостями служит линейный угол, образованныйдвумя прямыми – сечениями граней этого

Слайд 36

Слайд 37

Слайд 38Определение угла между скрещивающимися прямыми

угол между скрещивающимися прямыми называется угол,

который
образуется между прямыми, проведенными из произвольной точки
пространства параллельно данным скрещивающимся

прямыми

Определение угла между скрещивающимися прямымиугол между скрещивающимися прямыми называется угол, которыйобразуется между прямыми, проведенными из произвольной точкипространства

Слайд 39Позиционные задачи
задачи на принадлежность:
принадлежность точки линии,
принадлежность точки поверхности,
принадлежность линии поверхности.

задачи

на пересечение:
пересечение линии с линией,
пересечение поверхностей,
пересечение линии с поверхностью.
К позиционным

относятся задачи, решение которых в конечном счете, сводится:
- к построению точки принадлежащей линии,
- к построению точки, принадлежащей поверхности.

Позиционные задачизадачи на принадлежность:принадлежность точки линии,принадлежность точки поверхности,принадлежность линии поверхности.задачи на пересечение:пересечение линии с линией,пересечение поверхностей,пересечение линии

Слайд 40Принадлежность точки линии

Принадлежность точки линии

Слайд 41Принадлежность точки поверхности

Принадлежность точки поверхности

Слайд 42Принадлежность точки поверхности

Принадлежность точки поверхности

Слайд 43Принадлежность точки поверхности

Принадлежность точки поверхности

Слайд 44Принадлежность точки поверхности

Принадлежность точки поверхности

Слайд 45Принадлежность точки поверхности

Принадлежность точки поверхности

Слайд 46Принадлежность линии поверхности

Принадлежность линии поверхности

Слайд 47Пересечение линии с линией

Пересечение линии с линией

Слайд 48Пересечение плоскостей

Пересечение плоскостей

Слайд 49Пересечение плоскостей

Пересечение плоскостей

Слайд 50Пересечение плоскостей

Пересечение плоскостей

Слайд 51

Слайд 52

Слайд 53

Слайд 54

Слайд 55

Слайд 56

Слайд 57

Слайд 58

Слайд 59

Слайд 60

Слайд 61

Слайд 62

Слайд 63

Слайд 64

Слайд 65

Слайд 66

Слайд 67

Слайд 68

Слайд 69

Слайд 70

Слайд 71

Слайд 72

Слайд 73

Слайд 74

Слайд 75

Слайд 76

Слайд 77

Слайд 78

Слайд 79

Слайд 80

Слайд 81

Слайд 82

Слайд 83

Слайд 84

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей