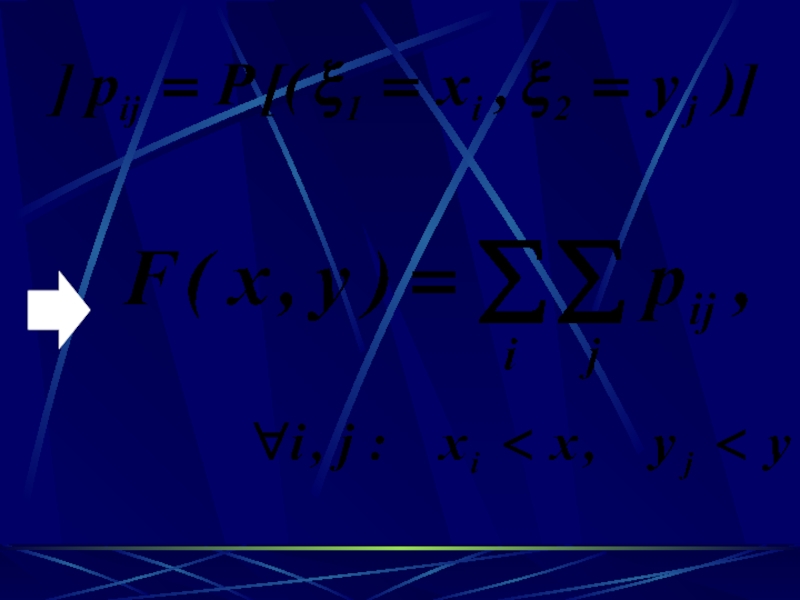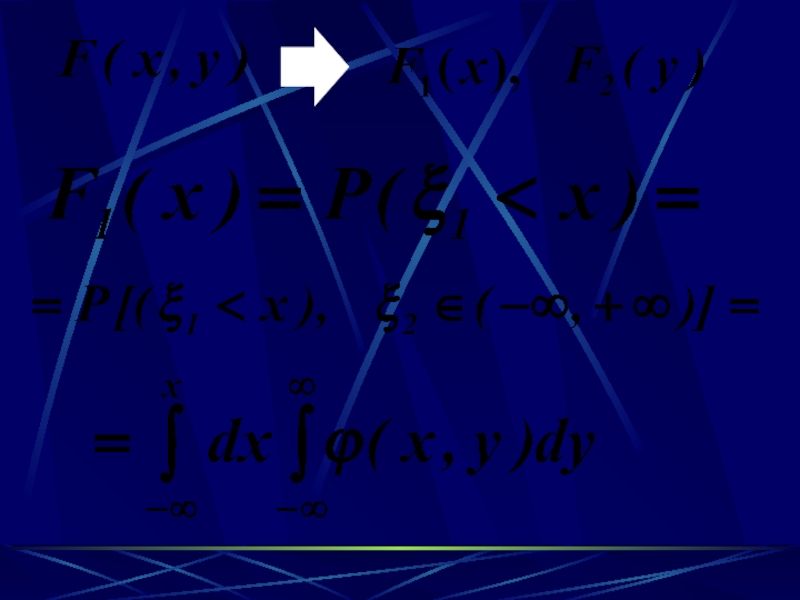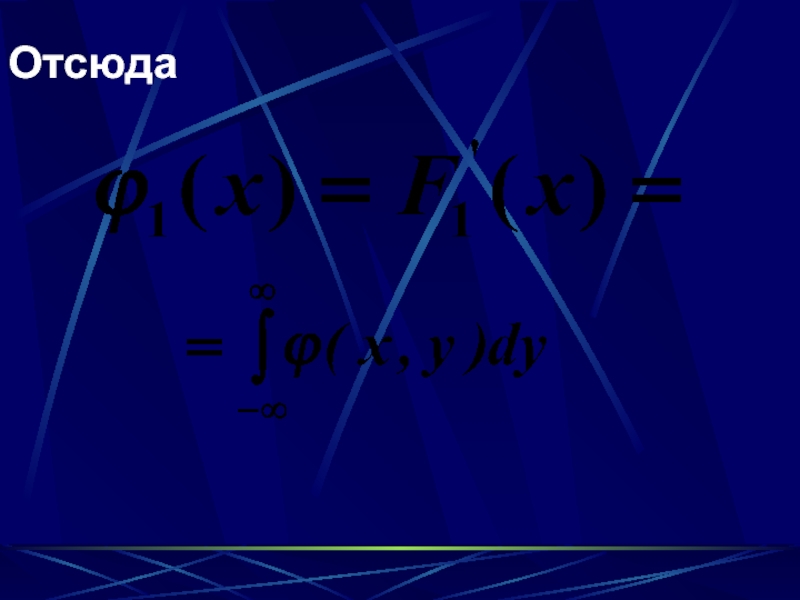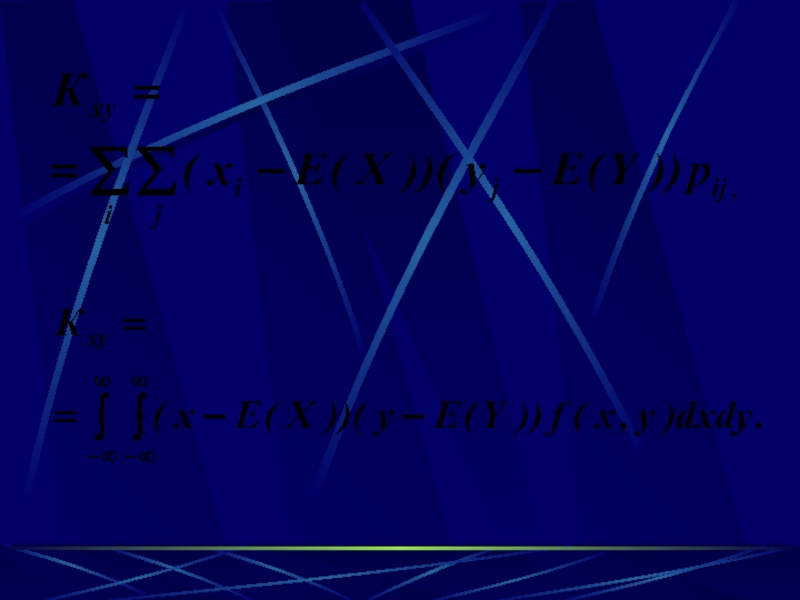Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая статистика
Содержание
- 1. Математическая статистика
- 2. Математическая статистика - наука, выявляющая закономерности повторяющихся
- 3. Основные задачи мат. статистики:1. Разработка методов анализа
- 4. Определения. Генеральная совокупность – все множество имеющихся наблюдений или объектов, относящихся к изучаемому явлению.
- 5. Выборка – набор наблюдений или объектов, случайно
- 6. Виды выборки Повторная – каждый отобранный объект
- 7. NB!Выборка должна быть репрезентативной (представительной).
- 8. Пусть с.в. Х принимает в выборке значение
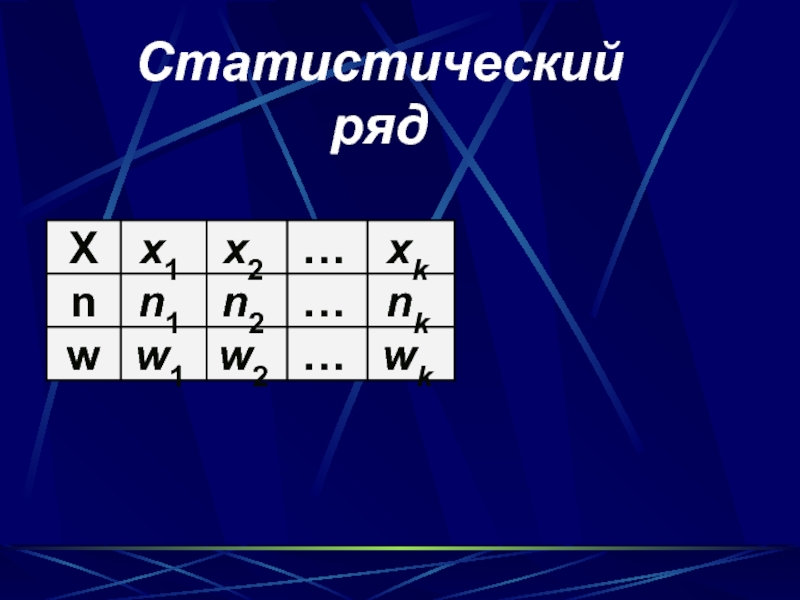
- 9. Статистический ряд
- 10. Пример.При проведении 20 бросков игральной кости число
- 11. Определение. Последовательность наблюдений, записанных в порядке возрастания или убываниях(1), х(2),…, х(к): х(1)= х(к)называют вариационным рядом.
- 12. Определение. Наблюдения, образующие вариационный ряд х(1), х(2),…,
- 13. ВОПРОС 30:Группированные данные
- 14. Статистический ряд для непрерывной с.в.
- 15. Полигон частот: ломаная, отрезки которой соединяют точки с координатами (x1, p1*), (x2, p2*),…, (xk, pk*) x
- 16. Выборочная функция распределения и гистограммаВОПРОС 31:
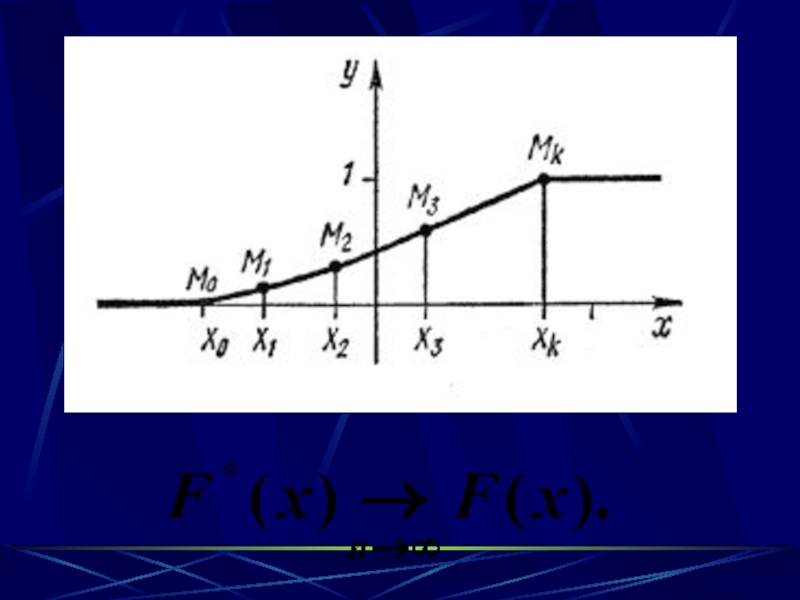
- 17. Определение. Выборочной (эмпирической) функцией распределения называют функцию
- 18. Слайд 18
- 19. Слайд 19
- 20. Свойства F*(x) (совпадают со свойствами F(x)):1.
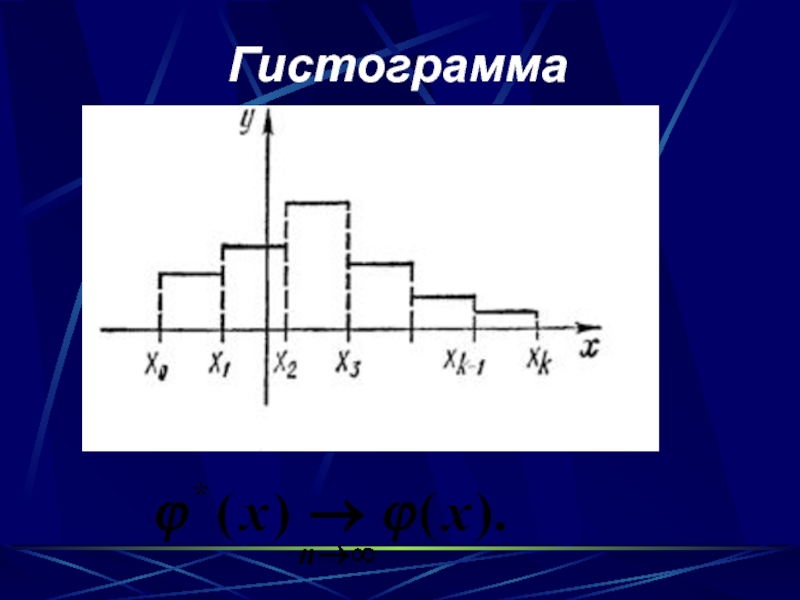
- 21. Эмпирическая плотность распределениякоторая в интервале ( Xi-1, Xi ] постоянна и равна
- 22. Гистограмма
- 23. ВОПРОС 32:Оценки параметра положения: выборочное среднее, оценки моды и медианы
- 24. ОПРЕДЕЛЕНИЯ. Выборочное среднее:
- 25. Мода:Медиана:
- 26. ВОПРОС 33:Оценки параметра масштаба: оценки дисперсии, начальных и центральных моментов
- 27. ОПРЕДЕЛЕНИЯ. Выборочной дисперсией называется
- 28. Центральный эмпирический момент:Начальный эмпирический момент:
- 29. Пример 1. Найти числовые характеристики выборки
- 30. Слайд 30
- 31. ВОПРОС 34:Свойства оценок
- 32. Схема: k выборок одного и того же
- 33. Слайд 33
- 34. Определение. Оценка некоторого признака называется АСИМПТОТИЧЕСКИ НЕСМЕЩЕННОЙ, если для выборки х1, х2, …, хп
- 35. Определение. Статистическая оценка называется ЭФФЕКТИВНОЙ, если она при заданном объеме выборки n имеет наименьшую возможную дисперсию
- 36. Определение. СОСТОЯТЕЛЬНОЙ называется статистическая оценка, которая при стремится по вероятности к оцениваемому параметру :
- 37. Теорема. Выборочное среднее представляет собой несмещенную оценку математического ожидания E(Х). Доказать самостоятельно!
- 38. Выборочное дисперсия представляет собой смещенную оценку дисперсии:
- 39. Исправленная выборочная дисперсия:
- 40. Исправленное среднее квадратическое отклонение
- 41. Определение. Оценка некоторого признака называется асимптотически несмещенной, если для выборки х1, х2, …, хn
- 42. СПОСОБЫ ПОСТРОЕНИЯ ОЦЕНОК
- 43. ВОПРОС 35:Метод максимального правдоподобия
- 44. Модель. ] Х – дискретная с.в., которая
- 45. Определение. Назовем функцией правдоподобия дискретной случайной величины
- 46. Определение. Оценкой наибольшего правдоподобия называется оценка при
- 47. Алгоритм поиска ММП-оценки: ММП-оценки состоятельны (хотя могут
- 48. ВОПРОС 36:Метод моментов
- 49. ] известный вид п.р. f(x, Θ1, Θ2
- 50. ВОПРОС 37:Метод наименьших квадратов
- 51. …)
- 52. Пример: y=ax+b
- 53. Слайд 53
- 54. ВОПРОС 38:Байесовский подход к получению оценок
- 55. ](Y, X) – случайный вектор, для которого
- 56. ДВУМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
- 57. ВОПРОС 39:Двумерные случайные величины
- 58. Определение. Двумерной случайной величиной называют систему из
- 59. Определение. Функция двух переменных определенная для любых
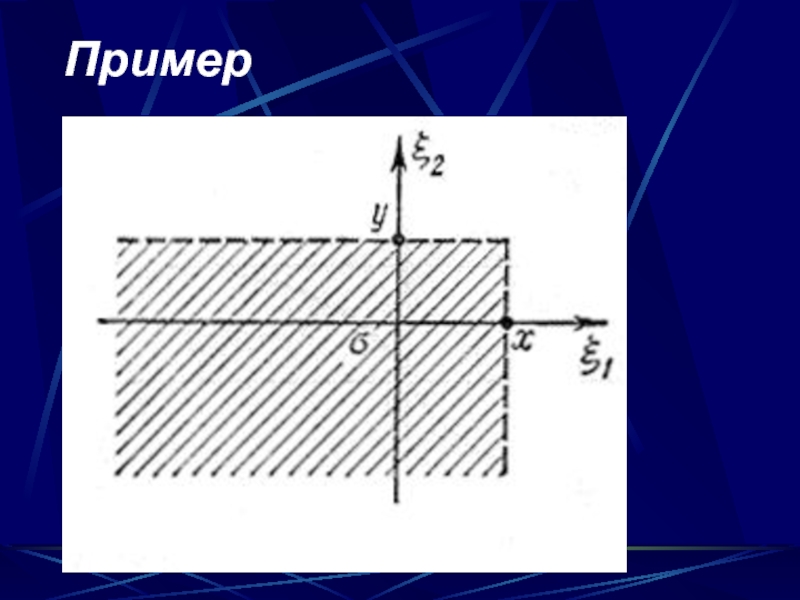
- 60. Пример
- 61. ДИСКРЕТНАЯ ДВУМЕРНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА Определение. Двумерная случайная
- 62. Слайд 62
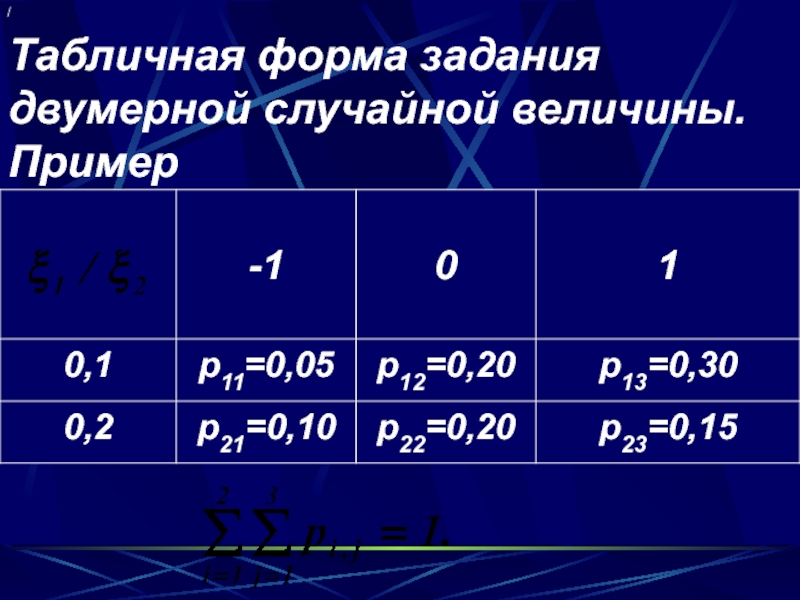
- 63. Табличная форма задания двумерной случайной величины. Пример /
- 64. Определение. Две дискретные случайные величины называются независимыми, если
- 65. Пример.
- 66. НЕПРЕРЫВНАЯ ДВУМЕРНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНАОпределение. Двумерная случайная величина называется непрерывной, если
- 67. Определение. Функция называется плотностью распределения вероятностей системы двух величин
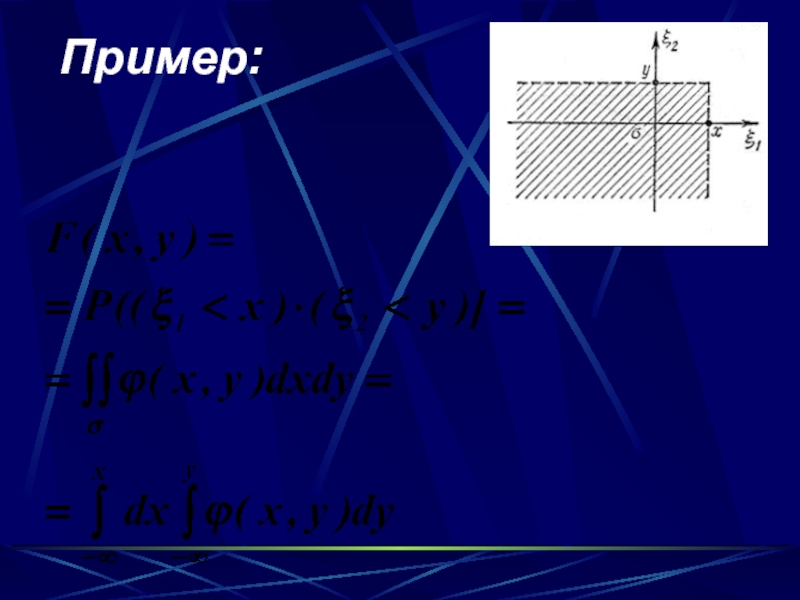
- 68. Пример:
- 69. Слайд 69
- 70. Для независимых с.в.
- 71. Слайд 71
- 72. Отсюда
- 73. Аналогично:
- 74. Пример
- 75. Определение. Двумерная случайная величина распределена нормально, если плотность распределения системы имеет вид:
- 76. Для независимых с.в.
- 77. ВОПРОС 40:Числовые характеристики двумерных случайных величин
- 78. Определение. Начальным моментом порядка (k, s) двумерной случайной величины (Х, Y) называется
- 79. Определение. Центральным моментом порядка (k, s) двумерной случайной величины (Х, Y) называется
- 80. При этом E(Х) = α1,0, E(Y) = α0,1, D(X) = μ2,0, D(Y) = μ0,2.
- 81. ВОПРОС 41:Корреляционный момент и коэффициент корреляции
- 82. Определение. Корреляционным моментом системы двух случайных величин
- 83. Слайд 83
- 84. Безразмерной характеристикой коррелированности двух случайных величин является коэффициент корреляцииОпределение.
- 85. Для независимых Х и Y f(x =f1(x)f2(y), тогда Теорема.
- 86. Доказательство
- 87. ВОПРОС 44:Статистическое описание и вычисление характеристик двумерного случайного вектора
- 88. Двумерная выборка представляет собой набор значений случайного
- 89. ВИДЫ ЗАВИСИМОСТЕЙ: : - функциональная зависимость, если
- 90. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Математическая статистика - наука, выявляющая закономерности повторяющихся случайных явлений на
основе обработки статистических данных, полученных в результате наблюдений.
Слайд 3Основные задачи мат. статистики:
1. Разработка методов анализа наблюдаемых случайных данных
( оценка неизвестной вероятности события, неизвестной функции распределения и ее
параметров, оценка зависимостей от случайных величин и т.д., проверка статистических гипотез);2. Синтез алгоритмов для решения задач выявления взаимосвязей, трендов, прогнозирования, поддержки принятия решений.
Слайд 4Определения.
Генеральная совокупность – все множество имеющихся наблюдений или объектов,
относящихся к изучаемому явлению.
Слайд 5Выборка – набор наблюдений или объектов, случайно отобранных из генеральной
совокупности.
Объем генеральной совокупности N и объем выборки n – число
наблюдений или объектов в рассматриваемых совокупностяхСлайд 6Виды выборки
Повторная – каждый отобранный объект перед выбором следующего
возвращается в генеральную совокупность;
Бесповторная – отобранный объект в генеральную совокупность
не возвращается.Слайд 8Пусть с.в. Х принимает в выборке значение х1 n1 раз,
х2 – n2 раз, …, хк – nк раз, причем
n – объем выборки.
Тогда наблюдаемые значения случайной величины х1,х2,…,хк называют наблюдениями, а n1, n2,…, nк – частотами.
Относительные частоты
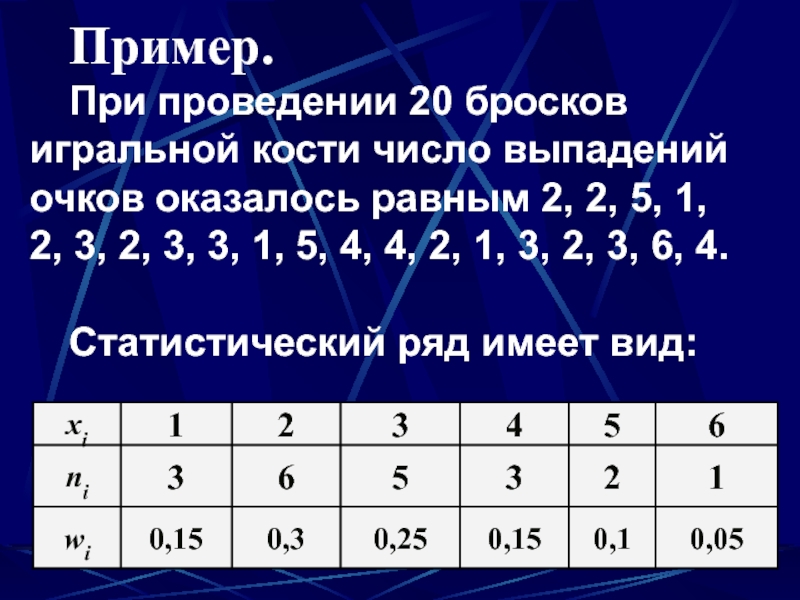
Слайд 10Пример.
При проведении 20 бросков игральной кости число выпадений очков оказалось
равным 2, 2, 5, 1, 2, 3, 2, 3, 3,
1, 5, 4, 4, 2, 1, 3, 2, 3, 6, 4.Статистический ряд имеет вид:
Слайд 11Определение.
Последовательность наблюдений, записанных в порядке возрастания или убывания
х(1), х(2),…,
х(к):
х(1)
или убываниях(1), х(2),…, х(к): х(1) >= х(2)>=… >= х(к)
называют вариационным рядом.
Слайд 12Определение.
Наблюдения, образующие вариационный ряд
х(1), х(2),…, х(к),
называются
порядковыми статистиками,
а
их номера в вариационном ряду – рангами.
Слайд 15Полигон частот:
ломаная, отрезки которой соединяют точки с координатами
(x1,
p1*), (x2, p2*),…, (xk, pk*)
x
Слайд 17Определение.
Выборочной (эмпирической) функцией распределения называют функцию F*(x), определяющую для
каждого значения х относительную
частоту события X < x:
Слайд 20Свойства F*(x)
(совпадают со свойствами F(x)):
1. 0 ≤ F*(x)
≤ 1.
2. F*(x) – неубывающая функция.
Если х1 – наименьшее наблюдение,
то F*(x) = 0 при х≤ х1;
если хк – наибольшее наблюдение,
то F*(x) = 1 при х > хк
Слайд 34Определение. Оценка некоторого признака называется АСИМПТОТИЧЕСКИ НЕСМЕЩЕННОЙ, если для выборки
х1, х2, …, хп
Слайд 35Определение. Статистическая оценка называется ЭФФЕКТИВНОЙ, если она при заданном объеме
выборки n имеет наименьшую возможную дисперсию
Слайд 36Определение. СОСТОЯТЕЛЬНОЙ называется статистическая оценка, которая при
стремится по
вероятности к оцениваемому параметру :
Слайд 37Теорема.
Выборочное среднее представляет собой несмещенную оценку математического ожидания E(Х).
Доказать самостоятельно!
Слайд 41Определение. Оценка некоторого признака называется асимптотически несмещенной, если для выборки
х1, х2, …, хn
Слайд 44Модель. ] Х – дискретная с.в., которая в результате п
испытаний приняла значения х1, х2, …, хп.
Предположим, что нам
известен закон распределения этой величины, определяемый параметром Θ, но неизвестно численное значение этого параметра. Найдем его точечную оценку.] р(хi, Θ) – вероятность того, что в результате i-го испытания величина Х примет значение хi.
Слайд 45Определение. Назовем функцией правдоподобия дискретной случайной величины Х функцию аргумента
Θ, определяемую по формуле:
L (х1, х2, …, хп; Θ)
= =p(x1,Θ)p(x2,Θ) … p(xn,Θ).L (х1, х2, …, хп; Θ) = f(x1,Θ)f(x2,Θ)…f(xn,Θ).
Слайд 46Определение. Оценкой наибольшего правдоподобия называется оценка
при котором функция
правдоподобия достигает максимума:
ln L – логарифмическая функция правдоподобия.
Слайд 47Алгоритм поиска ММП-оценки:
ММП-оценки состоятельны (хотя могут быть смещенными), распределены
асимптотически нормально и имеют наименьшую дисперсию по сравнению с другими
асимптотически нормальными оценками.Слайд 49] известный вид п.р. f(x, Θ1, Θ2 ) определяется двумя
неизвестными параметрами Θ1 и Θ2.
Требуется составить два уравнения, например
Θ1 = М1, Θ2 = т2. Отсюда
Решениями будут точечные оценки
Θ1 = ψ1 (х1, х2, …, хп),
Θ2 = ψ2(х1, х2, …, хп).
Слайд 55](Y, X) – случайный вектор,
для которого известна плотность р(Y|x)
.
Для оценки некоторой заданной функции φ(х) в качестве ее приближенного
значения предлагается искать условное математическое ожидание E( φ(х) |Y), вычисляемое по формуле где
Слайд 58Определение.
Двумерной случайной величиной называют систему из двух случайных величин
для которой определена вероятность
совместного выполнения неравенств
Слайд 59Определение.
Функция двух переменных
определенная для любых x и y,
называется функцией распределения системы двух случайных величин
Слайд 61ДИСКРЕТНАЯ ДВУМЕРНАЯ
СЛУЧАЙНАЯ ВЕЛИЧИНА
Определение.
Двумерная случайная величина
называется дискретной,
если
- дискретные величины.
Слайд 66НЕПРЕРЫВНАЯ ДВУМЕРНАЯ
СЛУЧАЙНАЯ ВЕЛИЧИНА
Определение.
Двумерная случайная величина
называется непрерывной, если
Слайд 75Определение.
Двумерная случайная величина распределена нормально, если плотность распределения системы
имеет вид:
Слайд 78Определение.
Начальным моментом порядка (k, s) двумерной случайной величины (Х,
Y) называется
Слайд 79Определение.
Центральным моментом порядка (k, s) двумерной случайной величины (Х,
Y) называется
Слайд 82Определение.
Корреляционным моментом системы двух случайных величин называется второй смешанный
центральный момент
Kxy = μ1,1 = E((X – EX)(Y –
EY)).Слайд 84Безразмерной характеристикой коррелированности двух случайных величин является коэффициент корреляции
Определение.
Слайд 88Двумерная выборка представляет собой набор значений случайного вектора:
(х1, у1),
(х2, у2), …, (хn, уn).
Дескриптивный статистический анализ:















![Математическая статистика Эмпирическая плотность распределениякоторая в интервале ( Xi-1, Xi ] постоянна и равна Эмпирическая плотность распределениякоторая в интервале ( Xi-1, Xi ] постоянна и равна](/img/thumbs/b87a4b01c53c9c5e9687287a7b40ad91-800x.jpg)





















![Математическая статистика Модель. ] Х – дискретная с.в., которая в результате п испытаний Модель. ] Х – дискретная с.в., которая в результате п испытаний приняла значения х1, х2, …, хп.](/img/thumbs/26c4e6e5a40434b7e3ade3539efd42e0-800x.jpg)




![Математическая статистика ] известный вид п.р. f(x, Θ1, Θ2 ) определяется двумя неизвестными ] известный вид п.р. f(x, Θ1, Θ2 ) определяется двумя неизвестными параметрами Θ1 и Θ2. Требуется составить](/img/thumbs/43bfe192c0c2ece55417dd98f5e576af-800x.jpg)





 – случайный вектор, для которого известна плотность р(Y|x) .Для ](Y, X) – случайный вектор, для которого известна плотность р(Y|x) .Для оценки некоторой заданной функции φ(х) в](/img/thumbs/54e3f4e4fe18cd066590c33ce4c5ee53-800x.jpg)