Слайд 2Лекция 12. ОСНОВНЫЕ ПОНЯТИЯ, ЕДИНИЦЫ И ПАРАМЕТРЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И
ТЕРМОДИНАМИКИ.
1. Основные понятия и определения молекулярной физики и термодинамики.
2. Давление.
Основное уравнение молекулярно-кинетической теории.
3. Температура. Единицы измерения температуры.
4. Изопроцессы идеальных газов.
5. Уравнение состояния газа (уравнение Менделеева-Клапейрона).
Слайд 31. Основные понятия
и определения молекулярной физики и термодинамики
Статистический и
термодинамический методы исследования. Молекулярная физика и термодинамика - разделы физики,
в которых изучаются макроскопические процессов телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики.
Слайд 4 Молекулярная физика – раздел физики, изучающий свойства тел в зависимости
от характера движения и взаимодействия частиц, образующих тело.
Идея об атомном
строении вещества высказана древнегреческим философом Демокритом (460 - 370 гг. до н. э.). Атомистика возрождается вновь лишь в XVII в. и развивается в работах М. В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относится к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса (1822 - 1888), английского физика Дж. Максвелла (1831-1879) и австрийского физика Л. Больцмана (1844-1906).
Слайд 5Процессы, изучаемые молекулярной физикой, являются результатом действия огромного числа молекул.
Свойства большого числа молекул отличны от свойств каждой отдельной молекулы
и подчиняются статистическим закономерностям. Они изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью беспорядочного движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул.
Слайд 6Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики
тел имеют физический смысл лишь в случае большого числа молекул.
Термодинамика
- раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах - фундаментальных законах, установленных в результате обобщения опытных данных.
Слайд 7Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет
таких областей физики и химии, в которых нельзя было бы
пользоваться термодинамическим методом. Однако, с другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между .макроскопическими свойствами вещества. Молеку-лярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, но отличаясь различными методами исследования.
Слайд 8Термодинамика анализирует условия и количественные соотношения превращения энергии.
Термодинамика имеет дело
с термодинамической системой - совокупностью макроскопических тел, которые взаимодействуют и
обмениваются энергией как между собой, так и с другими телами (внешней средой). Основа термодинамического метода — определение состояния термодинамической системы.
Слайд 9Состояние системы задается термодинамическими параметрами (параметрами состояния) — совокупностью физических
величин, характеризующих свойства термодинамической системы.
Обычно в качестве параметров состояния
выбирают температуру, давление и удельный объем.
Слайд 10Температура — одно из основных понятий, играющих важную роль не
только в термодинамике, но и в физике в целом.
Температура тела
- физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В соответствии с решением XI Генеральной конференции по мерам и весам (1960) в настоящее время можно применять только две температурные шкалы — термодинамическую и Международную практическую, - градуированные соответственно в Кельвинах (К) и в градусах Цельсия (°С).
Слайд 11В Международной практической шкале температура замерзания и кипения воды при
давлении 1,0135 Па принимается равной соответственно 0 и 100 °С
(так называемые реперные точки).
Термодинамическая температурная шкала используется в физике с 1954 г. Эта шкала определяется по одной реперной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщающий пар при давлении 609 Па находятся в термодинамическом равновесии). Температура этой точки по термодинамической шкале равна 273,16 К (точно). Градус Цельсия равен кельвину. В термодинамической шкале температура замерзания воды 273,15 К (при том же давлении, что и в Международной практической шкале),
Слайд 12Поэтому, по определению, термодинамическая температура и температура по Международной практической
шкале связаны соотношением Т = 273,15 + t. Температура Т
= 0 называется нулем кельвин. Анализ различных процессов показывает, что нуль кельвин недостижим, хотя приближение к нему сколь угодно близко возможно.
Удельный объем υ - величина, равная отношению объема V тела к его массе m. Когда тело однородно, т. е. его плотность ρ = const, то υ = V/m = 1/ρ. Так как при постоянной массе удельный объем пропорционален общему объему, то макроскопические свойства однородного тела можно характеризовать общим объёмом тела.
Слайд 13Параметры состояния системы могут изменяться. Любое изменение в термодинамической системе,
связанное с изменением хотя бы одного из ее термодинамических параметров,
называется термодинамическим процессом. Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не меняются).
Слайд 14 Термодинамическое равновесие существенно отличается от механического тем, что хотя параметры
системы остаются неизменными, частицы, из которых состоит система, находятся в
непрерывном движении.
Например, рассмотрим газ равномерно распределенный по всему объему. Но даже при большом числе молекул, некоторые области отклоняются от равномерного распределения.
Слайд 15 Исторически раньше сложилась термодинамика, или общая теория теплоты. Термодинамика является
феноменологической наукой. Она не вводит никаких конкретных представлений и специальных
гипотез о строении вещества и физической природы теплоты. Ее выводы основаны на общих принципах или началах, являющихся обобщением опытных фактов.
Термодинамика – термин, не соответствующий сути. Точнее было бы название термостатика, так как ни в одно уравнение термодинамически равновесных процессов не входит время.
Молекулярная физика, напротив, исходят из представления об атомно-молекулярном строении вещества, рассматривает теплоту как беспорядочное движение атомов и молекул.
Слайд 16 Молекулярная физика, называется молекулярно – кинетической теорией строения вещества. Эта
теория базируется на законах классической механики. Однако число молекул в
любом теле невероятно велико: в газах ~1025 шт/м3, в жидкостях и твердых телах ~1028 шт/м3.
Вот тут то на помощь приходит статистический метод. Он основан на законах вероятности и математической статистики. Дело в том, что в совокупном движении огромного числа частиц, координаты и скорости которых в любой момент случайны, появляются определенные (статистические) закономерности. Молекулярная физика рассматривает поведение частиц в совокупности (статистически).
Слайд 17 Термодинамика возникла в XIX веке как теоретическая основа начавшей развиваться
теплотехники.
Её первоначальная задача – изучение закономерностей превращения тепла в работу
(в тепловых машинах). Основным содержанием современной физической термодинамики является изучение закономерностей тепловой формы движущейся материи и связанных с ней физических явлений. Тепловая форма движения материи – это хаотическое движение атомов и молекул в макроскопических телах.
Слайд 18 О тепловом движении можно говорить только в тех случаях, когда
рассматриваемая система является макроскопической, то есть состоит из огромного числа
атомов и молекул. Не имеет смысла говорить о тепловом движении, когда система состоит из одного или нескольких атомов.
Особое положение термодинамики связано с тем, что любая форма энергии при ее превращениях в конце концов переходит в тепловую форму движения материи: электрическая, механическая, химическая энергии становятся в конце концов тепловыми энергиями.
Слайд 19 Время перехода – время релаксации. Если равновесие установилось, то система
самопроизвольно не сможет выйти из него. Горячий камень опустили в
воду. Наступит равновесное состояние: температуры одинаковы, и сколько не жди, температура не увеличится.
Атомная единица массы (а.е.м.) – mед – единица массы, равная 1/12 массы изотопа углерода С12.
1 а.е.м. = mед = 1,66·10−27 кг
Атомная масса химического элемента А – есть отношение массы атома этого элемента к 1/12 изотопа углерода С12 (Атомная масса – безразмерная величина).
m0 = Аmед (12.1)
Слайд 20 Количество вещества, в котором содержится число молекул, равное числу атомов
в 12 г 12С (изотопа углерода) называется молем (в 12
кг – киломолем).
Число молекул в одном моле называется числом Авогадро
NА = 6,02·1023 моль−1 = 6,02·1026 кмоль− 1.
Молярная масса – масса одного моля (µ)
µ = АmедNА (12.2)
Слайд 21 При одинаковых температурах и давлениях все газы содержат в единице
объёма одинаковое число молекул. Число молекул, содержащихся в 1 м3
при нормальных условиях, называется числом Лошмидта:
NL = р0/kT0 = 2,68·1025 м−3.
Нормальные условия: p0 = 105 Па; Т0 = 273 К; k – постоянная Больцмана равная 1,38·10−23Дж/К.
Слайд 222. Давление. Основное уравнение молекулярно-кинетической теории
Рассмотрим подробнее, что представляет собой
один из основных параметров состояния давление (p). Ещё в 18
веке Даниил Бернулли предположил, что давление газа – есть следствие столкновения газовых молекул со стенками сосуда. Именно давление чаще всего является единственным сигналом присутствия газа. Вообще давление определяется по формуле:
(12.3)
Слайд 23 Вычислим давление, оказываемое газом на одну из стенок сосуда (рис.
12.1). Рассуждения простейшие, но конечная формула верна. Обозначим n –
концентрация молекул в сосуде; m0 – масса одной молекулы.
Каждая молекула обладает импульсом m0υx, но стенка получает импульс 2m0υx (при абсолютно-упругом ударе m0υx – (−m0υx) = 2m0υx). За время dt о стенку, площадью S, успеет удариться число молекул, которое заключено в объёме V.
n = Sυxdt. (12.4)
Слайд 24 Общий импульс, который получит стенка S:
(12.5)
Разделим обе части равенства на
S и dt:
(12.6)
то есть определили давление, как силу, действующую в
единицу времени на единицу площади:
p = dF/dS.
Наивно полагать, что все молекулы подлетают к стенке S (Рис. 12.1) с одной и той же скоростью υx.
Слайд 25 На самом деле молекулы имеют разные скорости, направленные в разные
стороны, то есть скорости газовых молекул – случайная величина.
Более точно
случайную величину характеризует среднеквадратичная величина. Поэтому под скоростью υx2 понимаем среднеквадратичную скорость. Вектор скорости, направленный произвольно, можно разложить на три составляющие:
<υ2>=<υ2x>+<υ2y>+<υ2z> (12.7)
Ни одной из этих проекций нельзя отдать предпочтение из-за хаотичного теплового движения молекул, т.е. <υ2x>=<υ2y>=<υ2z>. Следовательно, на другие стенки будет точно такое же давление.
Слайд 26 Тогда можно записать в общем случае:
(12.8)
т.е.
(12.9)
где 〈Ek〉 – средняя энергия одной молекулы. Это и есть основное уравнение молекулярно-кинетической теории газов.
Итак, давление газов определяется средней кинетической энергией поступательного движения молекул.
Слайд 27 Почему называется основное уравнение? Давление p – макроскопический параметр, связанный
с макроскопическими параметрами: массой, скоростью молекул, – основные характеристики. Иногда
за основное уравнение принимают p = nkT.
Единицы измерения давления:
1 Па = 1 Н/м2; 1 ат. = 9,8 Н/см2 = 98066 Па ≈ 105 Па
1 мм.рт.ст. = 1 Тор = 1/760 ат. = 133,3 Па
1 бар = 105 Па; 1 ат. = 0,98 бар.
Содержание
Слайд 283. Температура. Единицы изменения
температуры
Приведём в соприкосновение два тела: горячее и
холодное, через некоторое время их температуры сравняются. Что перешло от
одного тела к другому. Раньше, во времена Ломоносова и Лавуазье считали, что носителем тепла является некоторая жидкость – теплород. На самом деле – ничего не происходит, только изменяется средняя кинетическая энергия – энергия движения молекул, из которых состоят эти тела. Именно средняя кинетическая энергия атомов и молекул есть температура! И следовало бы температуру измерять в джоулях. Но мы по привычке измеряем температуру в градусах.
Модель: Изменение температуры вещества
Слайд 29 Чтобы связать единицу энергии с градусом, Больцман ввел коэффициент пропорциональности
k который впоследствии был назван его именем: k – постоянная
Больцмана равная 1,38·10−23 Дж·К−1
(12.10)
Формула (12.10) – для расчета на одну молекулу идеального газа.
(12.11)
где R – универсальная газовая постоянная. Тогда
(12.12)
Слайд 30 Следовательно
(12.13)
это уже для молярной массы и газа.
Так как температура определяется
средней энергией движения молекул, то она, как и давление, является
статистической величиной, то есть параметром, проявляющимся в результате совокупного действия огромного числа молекул. Поэтому не говорят: «температура одной молекулы», лучше сказать: «энергия одной молекулы, но температура газа».
Слайд 31 С учетом сказанного о температуре, основное уравнение молекулярно кинетической теории
можно записать по другому:
(12.14)
где
Тогда
р = nkT (12.15)
в таком виде основное уравнение молекулярно – кинетической теории употребляется чаще.
Слайд 32Единицы измерения температуры
Так как всегда, то и
Т не может быть отрицательной величиной. Поэтому в физике была
введена абсолютная шкала температур. В настоящее время используются следующие шкалы:
1. Шкала Кельвина. 1К – одна из основных единиц системы СИ.
2. Шкала Фаренгейта (немецкий физик 1724 г.) – точка таянья льда 32°F, точка кипения 212°F.
3. Шкала Цельсия (шведский физик 1842г.) – точка таянья льда 0°С, точка кипения 100°С.
0°С = 273,15 К.
Своеобразие температуры заключается в том, что она не аддитивна (аддитивный – получаемый сложением).
Слайд 33 Несколько терминов и понятий, широко используемых в термодинамике и молекулярной
физике.
Параметры состояния не остаются строго постоянными, а испытывают небольшие колебания
внутри своих равновесных состояний. Такие колебания называются флуктуациями.
Процесс – переход из одного равновесного состояния в другое.
Релаксация – возвращение системы в равновесное состояние. Если система выведена из состояния равновесия и предоставлена самой себе, т. е. не подвержена внешним воздействиям, то самопроизвольно происходит процесс перехода к равновесному состоянию.
Слайд 34 Если мысленно разбить тело на части, то температура всего тела
не равна сумме температур его частей (длина, объём, масса, сопротивление,
и так далее – аддитивные величины). Поэтому температуру нельзя измерять, сравнивая её с эталоном. Для измерения температуры издавна пользуются тем, что при изменении температуры, тела изменяют свои свойства. Поэтому для измерения температуры выбирают какое-то термометрическое вещество (ртуть, спирт и так далее) и определяют величину, характеризующую свойство вещества – термометрическую величину (длина столба ртути).
Слайд 35 Интервал изменения длины столбика ртути от температуры таяния льда до
температуры кипения разбили на 100 частей и 1/100 назвали градусом.
Современная
термометрия основана на шкале идеального газа, где в качестве термометрической величины используют давление. Шкала газового термометра – является абсолютной (Т = 0; р = 0).
Содержание
Слайд 364. Изопроцессы идеальных газов
Изопроцессы идеального газа – процессы, при
которых один из параметров остаётся неизменным.
1. Изохорический процесс. Закон Шарля.
V=const. Изохорическим процессом называется процесс, протекающий при постоянном объёме. Поведение газа при изохорическом процессе подчиняется закону Шарля: P/Т = const, который формулируется так: При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным.
График изохорического процесса на рТ диаграмме называется изохорой (рис. 12.2). Полезно знать график изохорического процесса на рТ и VT диаграммах.
Слайд 38 Если температура газа выражена в градусах Цельсия, то уравнение изохорического
процесса записывается в виде
V = V0(1 + αt), (12.17)
где
V0 – давление при 0 °С по Цельсию; α − температурный коэффициент давления газа равен 1/273 град−1. График такой зависимости на pТ диаграмме имеет вид, указанный на рис. 12.3.
Рис. 12.3
Т,K
Слайд 39 2. Изобарический процесс. Закон Гей – Люссака. р=const. Изобарическим процессом
называется процесс, протекающий при постоянном давлении. Поведение газа при изобарическом
процессе подчиняется закону Гей – Люсака: V/T=const, который формулируется так: при постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным.
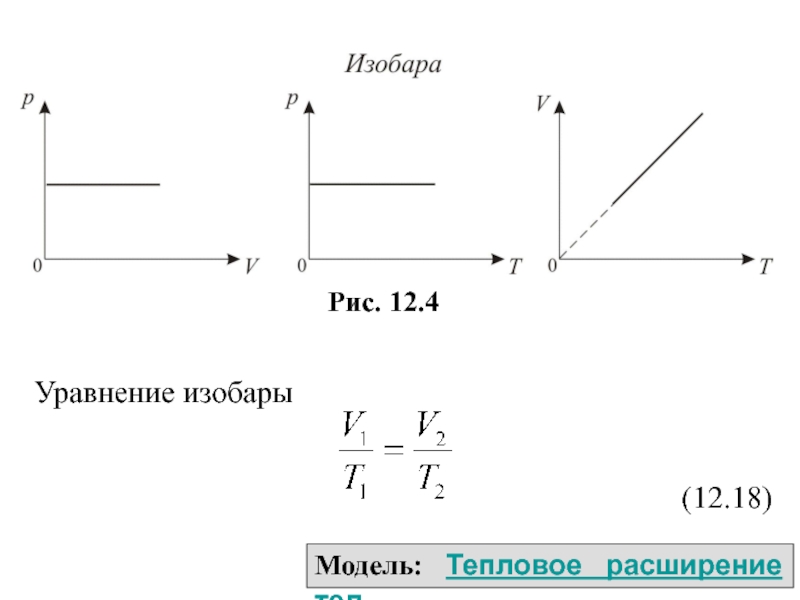
График изобарического процесса на VT диаграмме называется изобарой (рис. 12.4). Полезно знать графики изобарического процесса на рV и рT диаграммах.
Модель: Закон Гей-Люссака
Слайд 40Уравнение изобары
(12.18)
Модель: Тепловое расширение тел
Слайд 41 Если температура газа выражена в градусах Цель-сия, то уравнение изоба-рического
процесса записы-вается в виде
р=р0(1+αt), (12.19)
где р0 – давление
при 0 °С по Цельсию; α − температурный коэффициент давления газа равен 1/273 град−1. График такой зависимости на VТ диаграмме имеет вид, указан-ный на рисунке 12.5.
Рис. 12.5
V
Т,K
Слайд 42 3. Изотермический процесс. Закон Бойля-Мариотта. T=const.
Поведение идеального газа при изотермическом
процессе подчиняется закону Бойля – Мариотта: pV=const, который формулируется так:
при постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным. График изотермического процесса на pV–диаграмме называется изотермой (рис. 12.6).
Слайд 43 Полезно знать графики изотермического процесса на рV и рT диаграммах.
Уравнение изотермы
р1V1=р2V2.
(12.20)
Слайд 44 4. Адиабатический процесс (изоэнтропийный).
Адиабатический процесс – термодинамический процесс, происходящий без
теплообмена с окружающей средой.
5. Политропический процесс.
Политропический процесс – общий случай
всех перечисленных выше процессов. Процесс, при котором теплоёмкость газа остаётся постоянной.
Слайд 456. Закон Авогадро.
При одинаковых давлениях и одинаковых температурах, в равных
объёмах различных идеальных газов содержится одинаковое число молекул. В одном
моле различных веществ содержится
NA = 6,02·1023 молекул (число Авогадро).
Слайд 46 7. Закон Дальтона.
Давление смеси идеальных газов равно сумме парциальных давлений
р, входящих в неё газов
р = р1+ р2 +...+
рn (р1 – давление, которое оказывал бы определённый газ из смеси, если бы он занимал весь объём).
Слайд 47 8. Объединённый газовый закон (Закон Клапейрона).
В соответствии с законами Бойля
– Мариотта (12.20) и Гей – Люссака (12.18) можно сделать
заключение, что для данной массы газа
(12.22)
Содержание
Слайд 485. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
В молекулярно-кинетической теории пользуются
моделью идеального газа, удовлетворяющей следующим условиям:
1) собственный объём молекул газа
пренебрежимо мал по сравнению с объёмом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Слайд 49 Модель идеального газа можно использовать при изучении реальных газов, так
как они в условиях, близких к нормальным (например, кислород и
гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов.
Уравнение, связывающее основные параметры состояния идеального газа вывел великий русский ученый Д.И. Менделеев. Он объединил известные вам законы Бойля-Мариотта, Гей – Люсака и Шарля с законом Авогадро.
Слайд 50 Уравнение, связывающее все эти законы, называется уравнением Менделеева–Клапейрона и записывается
так:
(12.23)
где m – масса газа; μ – молярная масса газа;
R - универсальная газовая постоянная; V – объём газа; – число молей. Для одного моля можно записать рVμ = RT, или если обозначим – плотность газа, то
(12.24)
Слайд 51 Если рассматривать смесь газов, находящихся в объёме V при температуре
Т, то они имеют молярные массы и массы газов, заполняющие
объём (μ1, m1, μ2, m2). Мы вводим понятие – парциальное давление. Давление, которое оказывал бы данный газ, если бы он один занимал весь объём. Тогда:
(12.25)
и так далее.
Слайд 52 Согласно закону Дальтона: полное давление газа равно сумме парциальных давлений
всех газов, входящих в смесь р=р1+р2+...+рn. Отсюда, с учетом вышеизложенного,
можно записать
(12.26)
– это уравнение Менделеева–Клапейрона для смеси газов.