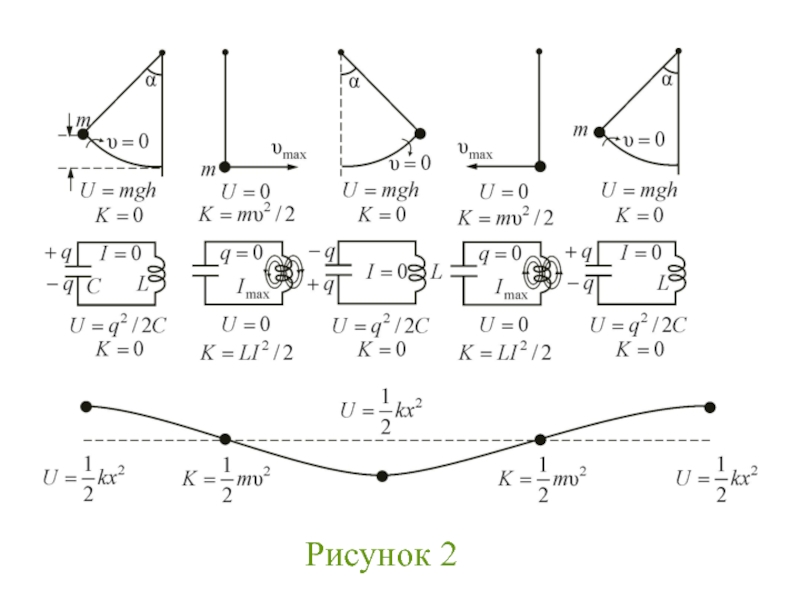
электрическом
контуре без активного сопротивления
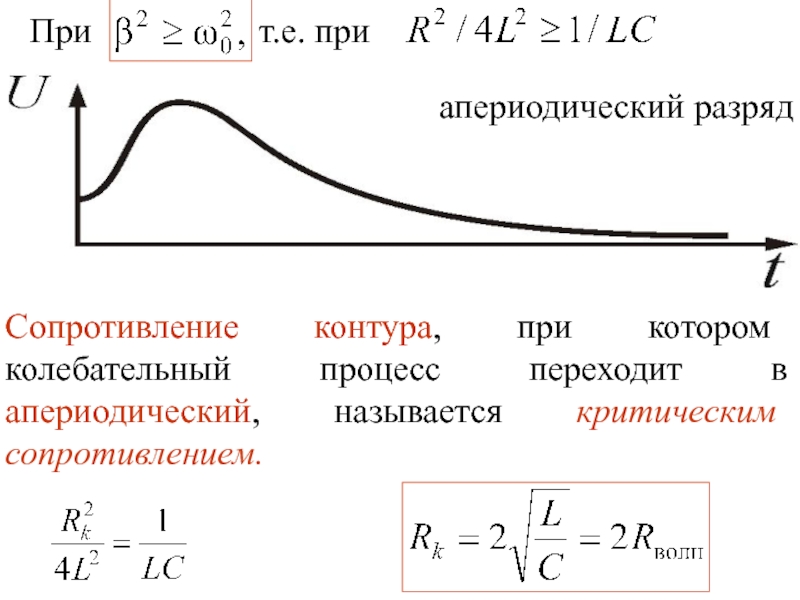
4.3 Свободные
затухающие электрическиеколебания
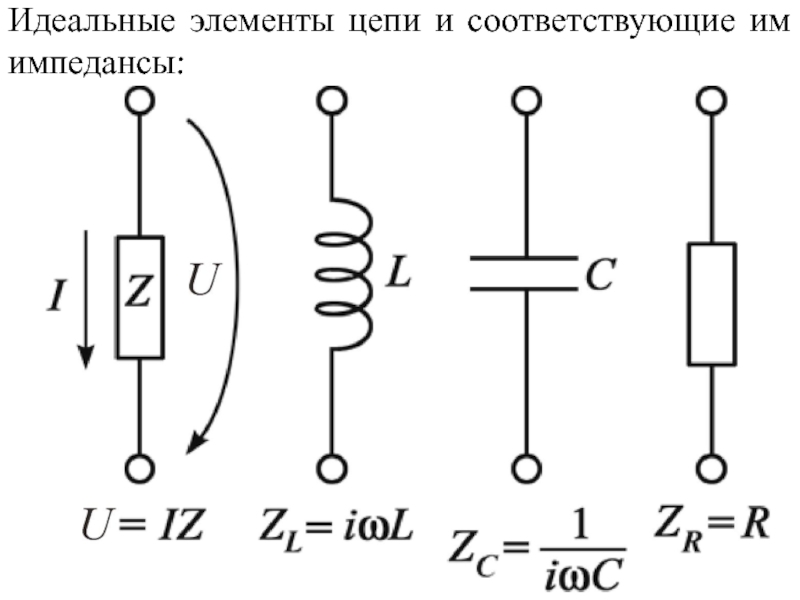
4.4 Вынужденные электрические колебания
Сегодня: *
4.5 Мощность, выделяемая в цепи
переменного тока