Слайд 1Самоподобие фракталов и степенные законы
Важным свойством фракталов
является их самоподобие.
Это означает, что структура фрактала
в одном масштабе подобна его структуре в другом, большем масштабе. Иными словами, увеличив в какое-то число раз любой элемент фрактальной структуры, мы получим элемент структуры того же фрактала.
Это свойство очевидно для точных, математических фракталов, с которыми мы познакомились выше.
Для случайных фракталов типа траектории броуновского движения, береговой линии или фрактальных кластеров, самоподобие нужно понимать статистически: увеличение случайного элемента фрактальной структуры дает случайный элемент структуры того же фрактала (см. увеличенный фрагмент траектории броуновской частицы)
Слайд 2Самоподобие означает, что в структуре фрактала отсутствуют какие-либо характерные размеры,
с которыми можно сравнить размеры ее элементов.
При
отсутствии характерных размеров система должна обладать одинаковыми свойствами во всех масштабах, так как ни одна область масштабов не выделена по сравнению с другими.
Поэтому часто самоподобие называют масштабной инвариантностью.
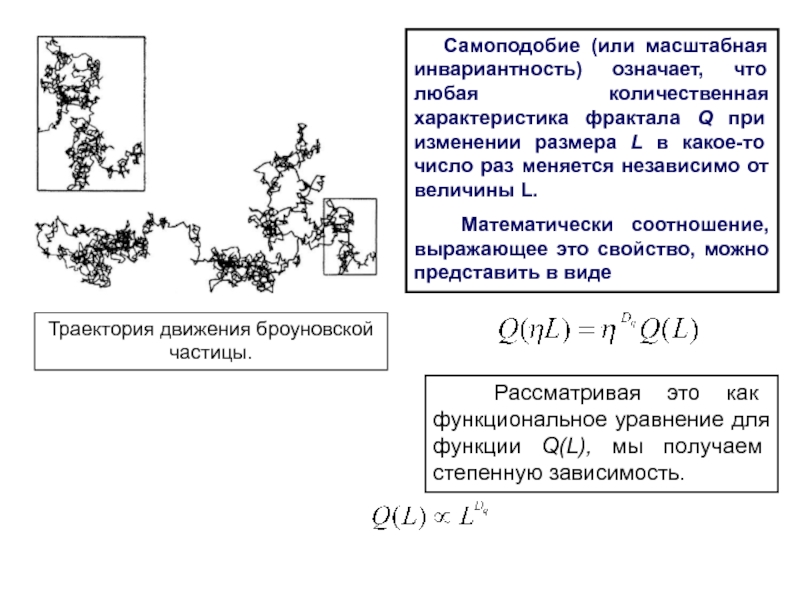
Слайд 3Траектория движения броуновской частицы.
Самоподобие (или масштабная инвариантность) означает,
что любая количественная характеристика фрактала Q при изменении размера L
в какое-то число раз меняется независимо от величины L.
Математически соотношение, выражающее это свойство, можно представить в виде
Рассматривая это как функциональное уравнение для функции Q(L), мы получаем степенную зависимость.
Слайд 4 Размерность Dq зависит, разумеется, от того, о какой
характеристике фрактала Q мы говорим.
Так, если Q
означает массу фрактала М с линейным размером L, то DM совпадает с хаусдорфовой размерностью D которую иногда по этой причине называют массовой размерностью.
Мы использовали уже это определение фрактальной размерности, когда говорили о распределении галактик во Вселенной.
Таким образом, самоподобие фракталов приводит к тому, что их свойства описываются степенными законами.
Слайд 5 Важным понятием фрактальной геометрии и фрактальной физики является
перколяция.
Бродбент и Хаммерсли рассмотрели общую ситуацию, возникающую
при случайном распространении жидкости через среду, когда абстрактные термины "жидкость" и "среда" могут быть интерпретированы в соответствии с физическим смыслом задачи.
В обычных процессах диффузии случайность есть не что иное, как случайные блуждания частиц жидкости.
Примером могут служить нерегулярное тепловое движение молекул в жидкости.
Другой пример случайности Хаммерсли назвал протеканием, или перколяционным процессом, поскольку жидкость в среде ведет себя, как вода в перколяторе (кофеварке).
Слайд 6 Диффундирующая частица в первом случае – обычной диффузии
- может достигать любой точки в среде.
Иначе
обстоит дело в случае перколяции.
Наиболее характерной особенностью перколяционных процессов является существование порога протекания, ниже которого процесс распространения жидкости ограничен конечной областью среды.
Жизненно важным примером является просачивание радиоактивных отходов в трещины и разломы горной породы.
Вопрос заключается в том, останется ли они локализованными в каком-то объеме или будут распространяться все дальше и дальше.
И в этой задаче можно ожидать, что существует критический порог концентрации трещин. Величину порога протекания можно определить с помощью численного моделирования.
Слайд 7 Для описания фрактальных структур, встречающихся на микро и
наномасштабах, широко используют понятие кластер.
Это - скопление близко расположенных,
тесно связанных друг с другом частиц любой природы (атомов, молекул, ионов, ультрадисперсных и наночастиц) общим количеством 2-100 частиц.
В последнее время термин кластер распространяется и на системы, состоящие из большого числа связанных макроскопических частиц.
Введено также понятие фрактального кластера, под которым понимают структуру, образующуюся в результате ассоциации частиц при условии диффузионного характера их движения.
Слайд 8 Основной чертой фрактального кластера является то, что средняя
плотность частиц в нем ρ(г) падает по мере удаления от
образующего центра по закону, где а - размер частицы, г- расстояние от центра.
ρ(r)= const / га
Связь между размером кластера и числом частиц N (или массой фрактала) можно представить в виде:
N ~ RD
где R - расстояние от центра кластера; D = d - а - фрактальная размерность кластера; d - размерность объемлющего пространства.
Слайд 9 Paзмерность кластерa D не зависит ни от его
формы, ни от типа упаковки в нем частиц.
Она лишь служит количественной характеристикой того, как кластер заполняет занимаемое им пространство.
Поскольку фрактальная система обладает свойством самоподобия, то его можно сформулировать следующим образом: если в окрестности точки, занятой кластером, выделить область относительно небольшого объема, то попадающие в него участки кластера будут подобны в физическом смысле.
Таким образом, фрактальный кластер, построенный по случайному закону, имеет внутренний порядок, а свойство самоподобия следует понимать статистически.
Слайд 10 Фрактальная размерность кластера служит количественной характеристикой того, как
кластер заполняет занимаемое им пространство.
Надо отчетливо понимать,
что если кластер пористый или случайный, то это отнюдь не означает, что он фрактальный.
Фрактальный кластер в большинстве случаев отличается тем свойством, что с ростом размером его плотность убывает по закону, описываемому показателем степени в соотношении число частиц - радиус.
Фрактальная размерность кластера в принципе не описывает его форму.
Слайд 11 Необходимо, однако, все время помнить, что фрактальные кластеры
одной размерности могут иметь несовпадающие другие характеристики, такие, как разветвленность.
В силу интерференционных явлений фрактальный кластер может быть эффективным поглотителем излучения для длин волн, сравнимых с его размерами.
Этот факт используется при нанесении покрытий на приемники инфракрасного излучения. Такие покрытия изготавливаются путем испарения металла и осаждения его на поверхность.
Слайд 12 С пористыми структурами также связано несколько странноватое для
нашего восприятия понятие вязких пальцев.
Проблема их образования
в пористых средах имеет первостепенное значение для добычи нефти.
Она представляет интерес и для гидродинамики, и для физики пористых сред.
Это явление связано с неустойчивостью фронта вытеснения в пористых средах, где сильно вязкая жидкость (например, нефть) вытесняется слабо вязкой жидкостью (водой).
Слайд 13 Граница раздела между двумя жидкостями в классическом случае
будет двигаться с постоянной скоростью вдоль нормали к границе раздела
сред.
Но если вязкость вытесняющей жидкости меньше вязкости вытесняемой жидкости, то граница раздела двух жидкостей оказывается неустойчивой.
Энгельбертс и Клинкенберг, описывая свои наблюдения такого рода неустойчивостей при вытеснении нефти водой в пористой среде, предложили термин "образование вязких пальцев".
Слайд 14 Физика процесса образования вязких пальцев определяется динамикой движения
границы.
Вследствие ее неустойчивости некоторые локальные области начнут
двигаться быстрее, образуя пальцы.
Предполагается также, что палец выступает в ту сторону, куда движется фронт вытеснения, опережая остальную его часть.
Следовательно, наибольший градиент давления в сильно вязкой жидкости образуется на конце пальца.
Этот большой градиент индуцирует максимальную скорость течения жидкости непосредственно перед самым длинным пальцем, который растет быстрее, чем фронт в среднем, а такая ситуация, как нетрудно видеть, неустойчива.
Как только этот самый большой палец достигнет определенных размеров, весь процесс повторяется на его границе, в результате чего образуется ветвистая структура.
Слайд 15 Саффмэн и Тейлор исследовали образование вязких пальцев на примерах
вытеснения глицерина воздухом. Начальная граница раздела имела мелкие нерегулярности, как
это показано на рисунке (а).
Поскольку давление воздуха одинаково, то эти нерегулярности начинают развиваться на средней стадии (б). На поздней стадии более длинные пальцы тормозят рост соседей (в).
К настоящему моменту теория развития вязких пальцев достаточно разработана и нашла применение для объяснения многих физических процессов, в частности пробоев диэлектриков, дендритному росту, процессам в пористых структурах и нефтяных скважинах.
Слайд 16 Слева в жидкий желатин впрыснуто через канюлю (черная
полоса на рисунке) некоторое количество подкрашенной воды (вода и желатин
хорошо смешиваются), а справа в желатин впрыснут раствор сахара (смешиваемость значительно хуже).
В случае несмешивающихся жидкостей языки гораздо шире, потому что поверхностное натяжение между этими двумя жидкостями препятствует образованию тонких дендритов, т.е. выступов с большой кривизной.
Когда в нефтяной пласт закачивают воду, до 60% нефти остается в закапсулированном виде в земле.
Форма языков зависит от степени взаимной смешиваемости жидкостей.
Слайд 18Реальные фракталы и методы определения фрактальной размерности.
Распространенность
фрактальных структур в природе, как было подмечено ранее, невообразима.
Фрактальны пористые минералы и горные породы; расположение ветвей, узоры листьев, капиллярная система растений; кровеносная, нервная, лимфатическая и др. системы в организмах животных и человека; реки, облака, линия морского побережья, горный рельеф и многое другое.
Мало того, фрактальны практически все поверхности твердых тел.
Слайд 19 В последнее время появляются теории фрактального строения и
принципов развития Вселенной, физического вакуума и много других разнообразных теорий.
Возникает естественный вопрос (не что делать или кто виноват) - как рассчитать фрактальную размерность реальных природных объектов или субъектов.
Фрактальная размерность математических фракталов вытекает автоматически из алгоритма их построения, а вот алгоритмы построения реальных физических структур нам пока, мягко говоря, недоступны.
Слайд 20 Тем не менее к настоящему времени уже разработано
довольно много методов измерения фрактальной размерности реальных объектов.
Их можно разделить на геометрические (метод островов среза, Фурье анализ профилей, метод вертикальных сечений, метод подсчета числа ячеек и пр.)
и физические, связанные с использованием на первой ступени сложной физической аппаратуры (ртутная порометрия, растровая электронная и просвечивающая электронная микроскопии, атомно-силовая микроскопия, вторичная электронная эмиссия, малоугловое рассеяние электронов и нейтронов и т.д.).
Слайд 21 Получаемая с помощью физических методов информация о характеристиках
объекта носит косвенный характер и требует дополнительной обработки и осмысления,
поэтому физические методы особой популярностью не пользуются.
Геометрические методы можно также условно разбить на два направления.
Первое направление занимается непосредственным измерением фрактальной размерности собственно самой фрактальной структуры.
Второе направление моделирует реальную фрактальную структуру с помощью известных математических структур или регулярных фракталов, фрактальная размерность которых уже известна и приписывает изучаемой фрактальной структуре характеристики структуры-модели.
Метод настолько же удобен, насколько неадекватен.
Слайд 22 Разработано множество модельных механизмов формирования фрактальных структур и
кластеров.
Это во многом связано с развитием и
все более широким внедрением вычислительной техники. Проведено огромное количество численных экспериментов, в которых выявлялись закономерности фрактальной природы реальных объектов на основе модельных механизмов.
Среди моделей агрегации следует выделить модель, ограниченной диффузией агрегации (ОДА или DLA), модель ограниченной диффузией кластерной агрегации (ОДКА - DLCA) и модель кластер-кластерной агрегации (ККА - ССА).
Слайд 23 Многие реальные физические процессы хорошо описываются ОДА -
моделью. Это прежде всего электролиз, кристаллизация жидкости на подложке, осаждение
частиц при напылении твердых аэрозолей.
В компьютерном моделировании ОДА- процесса на начальном этапе в центре области устанавливается затравочное зерно, затем из удаленного источника на границе области поочередно выпускаются частицы, которые совершают броуновское движение и в конечном итоге прилипают к неподвижному зерну. Таким образом происходит рост ОДА - кластера.
Фрактальный кластер, смоделированный по ОДА алгоритму
Хаотичная структура высушенного геля, полученного щелочным гидролизом кремнезема.
Слайд 24 При помощи ККА - процесса моделируются гелеобразование и
формирование связанно-дисперсных систем. В этом процессе нет затравочного зерна. Все
частицы совершают случайные блуждания и образуют кластеры, которые продолжают диффундировать, формируя кластеры больших размеров. В пределе система может превратиться в один гигантский кластер.
В развитых фрактальных структурах, образовавшихся в условиях самоорганизации и действия различных физических процессов возникает конкуренция нескольких центров за доминирование на плоскости или в объеме.
В результате такого соперничества редко возникают простые границы между территориями. Чаще происходит взаимопроникновение структур и их конкуренция за самые незначительные участки территории, что приводит к деформации и искажению нормальной структуры границы.
Пограничные области в большей или меньшей мере неоднородно и непредсказуемо зависят от условий, характеризующих изучаемый процесс.
Слайд 25 Может возникнуть и большее число конкурентов, что особенно
характерно для неоднородных фракталов и их структур.
Может
случиться, что один центр захватит всю локальную область и полностью на ней доминирует, но и в этом случае его доминирующее положение ограничено.
Подобного рода границы могут быть описаны исключительно фрактальной геометрией. Инструментом для описания подобных объектов служат фрактальные множества.
Расчет фрактальной размерности и других характеристик реальных объектов немыслим без применения современной компьютерной техники и компьютерных технологий.
Слайд 26 В зависимости от размера объекта (фрактального агрегата) его
изображение можно получить фотографированием в обычном оптическом, электронном растровом или
электронном просвечивающем микроскопе, сканирующем туннельно-зондовом или атомно-силовом микроскопе (три основные ступени увеличения исследуемого объекта).
Дальнейший анализ изображения для получения фрактальных характеристик сводится к тому, что поле изображения фотографии разбивается на конечное число элементов, в простейшем случае квадратиков или пикселей.
Слайд 27 Яркость изображения в пределах каждого элемента должна быть
одинаковой или хотя бы таковой считаться.
Минимальный размер
изображения определяется разрешающей способностью аппаратуры, что, в свою очередь, определяет качество фрактального анализа.
Оптимальным является случай, когда размер элемента изображения соответствует размеру частицы ρ, из которых затем образуется фрактальный агрегат.
Размер кадра или области сканирования должен приблизительно соответствовать размеру фрактального агрегата.
Число дискретных элементов изображения должно быть достаточно большим, чтобы масштабную инвариантность можно было проверить в достаточно широком диапазоне размеров. Поэтому желательно производить анализ структуры на всех трех уровнях, от оптической микроскопии по всем ступеням ее возможностей - и до атомно-силовой микроскопии.
Слайд 28 В тех случаях, когда фрактальные свойства проявляются
на масштабах, не превышающих 1 мкм, для измерений можно использовать
излучение с короткими длинами волн - рентгеновское или глубокий (вакуумный) ультрафиолет.
Геометрический метод весьма эффективно используется для природных ломаных форм типа описания броуновского движения.
Его использовали, чтобы вычислить размерности побережий, границ и облаков, микропористых структур и наноразмерных частиц.
Слайд 29 Метод подобия и геометрический метод для вычисления фрактальной
размерности требуют измерения размера.
Самым простым способом является
разбиение изображения объекта (микрофотографии или схемы границ) посредством координатной сетки на квадраты или пиксели, с размером стороны h.
Современная компьютерная техника позволяет это делать практически с любой точностью. Вместо нахождения точного размера фрактала, производится подсчет числа клеток, которые не пусты.
Приравняем к этому числу переменную N. Уменьшение клеток делает подсчет более точным, что равносильно увеличению изображения. Фактически увеличение е является равным 1/h. Тогда формулу для фрактальной размерности можно записать в виде:
D = log N / log e
Заменяем с учетом произведенного разбиения на:
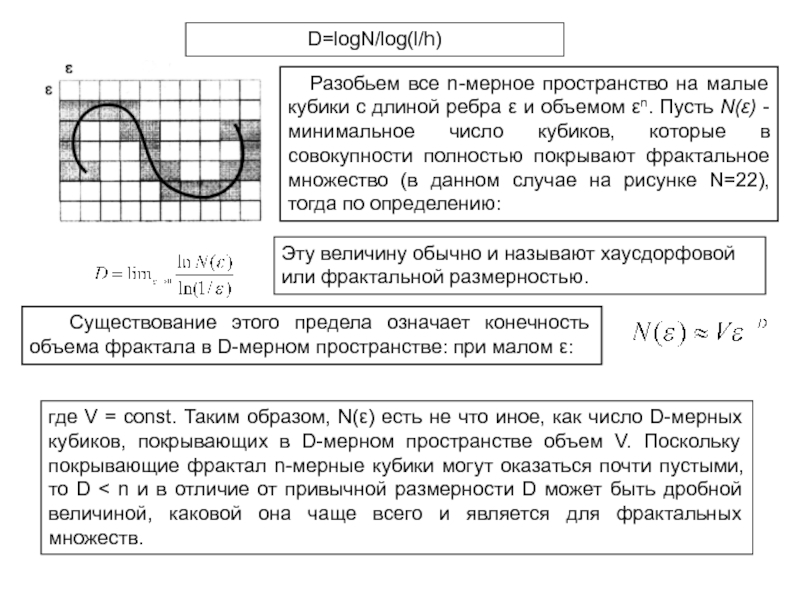
Слайд 30D=logN/log(l/h)
Разобьем все n-мерное пространство на малые кубики
с длиной ребра ε и объемом εn. Пусть N(ε) -
минимальное число кубиков, которые в совокупности полностью покрывают фрактальное множество (в данном случае на рисунке N=22), тогда по определению:
Эту величину обычно и называют хаусдорфовой или фрактальной размерностью.
Существование этого предела означает конечность объема фрактала в D-мерном пространстве: при малом ε:
где V = const. Таким образом, N(ε) есть не что иное, как число D-мерных кубиков, покрывающих в D-мерном пространстве объем V. Поскольку покрывающие фрактал n-мерные кубики могут оказаться почти пустыми, то D < n и в отличие от привычной размерности D может быть дробной величиной, каковой она чаще всего и является для фрактальных множеств.
Слайд 31 Уменьшение h будет делать величину получаемой размерности более
точной.
Для 3-х размерных фракталов аналогичную операцию можно
производить с кубами вместо квадратов, а для фракталов в одном измерении можно использовать отрезки.
Метод счета клеток применим для природных форм, которые с трудом поддаются измерению, от фрактальных наноразмерных пленок до культуры бактерий.
Слайд 32 К непрямым геометрическим методам относится метод вертикальных сечений, состоящий
в исследовании зависимости длины профиля поверхности разрушения от масштаба разрушения.
Максимальная достоверность достигается при анализе нескольких ориентаций профилей на обрабатываемой поверхности.
Профили получаются при шлифовании вертикальных сечений поверхности разрушения, покрытой твердым компаундом. Зависимость длины профилей L от масштаба измерения ε описывается уравнением:
где d=1 - целая размерность линии, D' - размерность профиля. В методе вертикальных сечений непосредственно измеряется наклон зависимости lnL(ε) от ln(ε), а размерность самой поверхности разрушения определяется по формуле:
Слайд 33
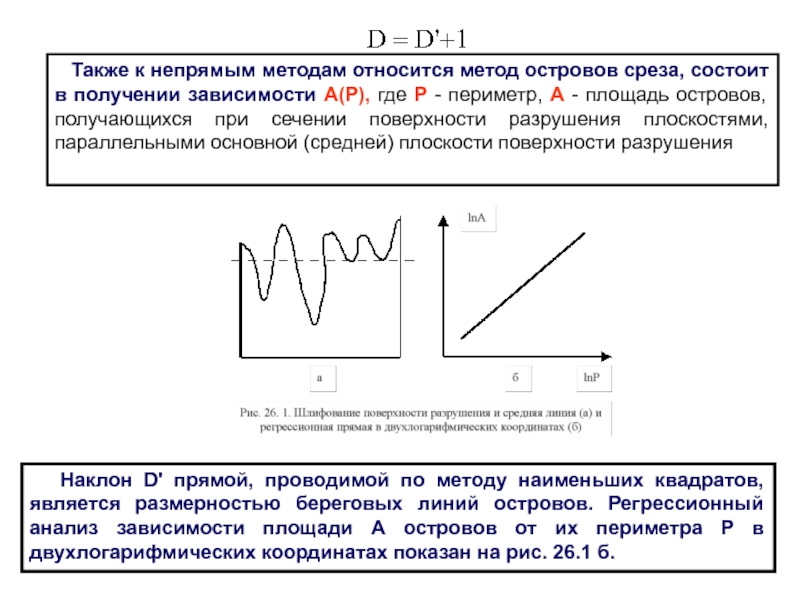
Также к непрямым методам относится метод островов среза,
состоит в получении зависимости А(Р), где Р - периметр, А
- площадь островов, получающихся при сечении поверхности разрушения плоскостями, параллельными основной (средней) плоскости поверхности разрушения
Наклон D' прямой, проводимой по методу наименьших квадратов, является размерностью береговых линий островов. Регрессионный анализ зависимости площади А островов от их периметра Р в двухлогарифмических координатах показан на рис. 26.1 б.
Слайд 34 Для получения таких срезов обычно применяется специальная технология,
достаточно варварская.
Поверхность разрушения сначала покрывают тонким слоем
электролитически выращенного никеля, образец заливается компаундом и после затвердения компаунда подвергается ступенчатой полировке.
Получаемые при этом последовательные шлифы обрабатываются тем или иным способом, чаще всего с помощью анализатора изображения, который выделяет границы островов срезанной верхушки поверхности разрушения, что дает статистику точек на плоскости lnP - lnA.
Образец, естественно, при этом безвозвратно уничтожается.
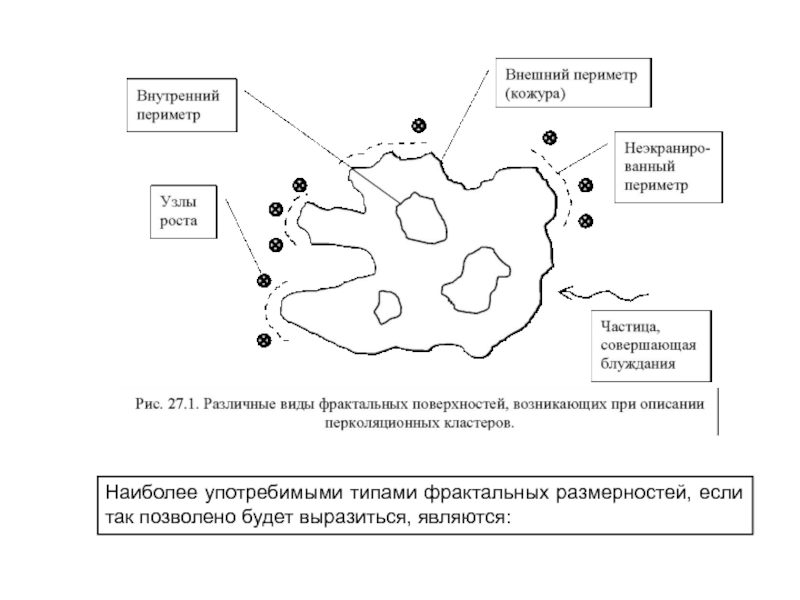
Слайд 35 Как показано на рис. 27.1, это может быть
внешний периметр Dh (иногда не совсем корректно с высоконаучной точки
зрения, зато понятно и доходчиво, его называют кожурой или скорлупой), полный периметр Df, и неэкранированный периметр Du.
Неэкранированный периметр (показан штриховой линией) сопоставляется с размерностью Du, - это области, где велика вероятность столкновения блуждающей частицы с границей кластера. Узлы роста образуют границу кластера, фрактальная размерность их множества Dg, а конкретный вид фрактала, образованного этими узлами, зависит от механизма роста кластера.
Для описания реальных объектов существует довольно большое множество различных типов фрактальных размерностей.
Если использовать модельную систему фрактального пористого (перколяционного) кластера то возникает вопрос, а что, собственно, понимать тогда под поверхностью, поскольку для нее возможно уже несколько определений, а не одно, как в случае классической физики.
Слайд 36Наиболее употребимыми типами фрактальных размерностей, если так позволено будет выразиться,
являются:
Слайд 37 1. Химическая фрактальная размерность Dхим, которая учитывает расположение
и величину всех химических связей, которые существуют между частицами кластера,
и определяется через соотношение:
2. Статистическая (массовая) фрактальная размерность объекта Dстат, характеризующая распределение всех узлов кластера в пространстве и является фрактальной размерностью в обычном понимании.
3. Фрактальная размерность узлов роста Dg, характеризующая пространственное распределение узлов, к которым далее могут присоединяться частицы в процессе роста кластера. Иногда ее называют фрактальной размерностью периметра роста.
4. Фрактальная размерность неэкранированной части поверхности Du
5. Фрактальная размерность минимального пути для блуждающей частицы, помещенной на кластер Dмин .
где N - число узлов (частиц) в кластере, а L - длина химических связей между узлами.
Слайд 38 Физические методы измерения размерности менее популярны вследствие их
технической сложности и необходимости иметь высококвалифицированный персонал и современное оборудование.
И ФИНАНСИРОВАНИЕ.
Часто встречаются случаи, когда изучаемый материал имеет исключительно развитую внешнюю поверхность или сложную трехмерную структуру взаимосвязанных пор различного размера и формы. К ним относится значительное количество наноматериалов, включая нанопорошки, аэрогели, адсорбенты и пр.
Для них специально были введены новые структурно-чувствительные параметры: поверхностная фрактальная размерность Dfs (наружная поверхность или поверхность пор) и фрактальная размерность порового объемного пространства Dfv. Методы их определения являются отчасти калькой метода подсчета клеток (считаются либо молекулы и атомы адсорбата, либо используется связанное с ними какое-либо физическое свойство).
Слайд 39 Одним из старых методов, обретшим новую фрактальную жизнь,
является метод ртутной порометрии.
В этом методе в исследуемый пористый
образец нагнетается или вдавливается жидкость с углом смачивания более 90° (ртуть, расплавленный сплав Вуда, глицерин) и измеряется зависимость объема вдавленной жидкости от внешнего давления.
Ртуть привлекательна тем, что изменение объема вдавленной жидкости определяется по изменению электрического сопротивления проволоки, погруженной в жидкость на достаточном удалении от образца (экологические и медицинские аспекты, связанные с таким приятным и полезным веществом, как ртуть, во внимание как-то не принимаются).
Слайд 40 Для фрактальной параметризации пористых структур вводится понятие эффективного
геометрического объекта - скейла, с помощью которого можно моделировать структуру
материала с любой пористостью mε.
В этом случае под пористостью m понимают относительный объем порового пространства так, что m~0 для сред с малой пористостью (в пределе весь объем твердого тела - скелет материала), а m ~ 1 для сред с большой пористостью (в пределе - поровое пространство).
Скейл, сохраняя свойство самоподобия, не имеет фрактальной размерности, но характеризуется заданной пористостью m и степенным распределением числа пор по размерам.
Структуры реальных материалов являются исключительно сложными стохастическими образованиями (стохастическим фракталами), самоподобными только в определенных рамках масштаба. Поэтому однозначная корреляция между фрактальной размерностью структуры и ее механическими, электрофизическими и прочими свойствами пока не найдено.
Слайд 41 Надо признать, что наше мировосприятие пока не способно
осознавать как фрактальность структуры, так и оперировать с фрактальной размерностью.
Если мы легко отличаем, скажем толстого низенького лысого человека пожилого возраста (препода) от стройного высокого молодого лохматого балбеса (студента), то набор цифр соответствующих фрактальных размерностей, характеризующих фрактальный объект ничего не говорит ни уму, ни сердцу. Пока.