Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сложность задач
Содержание
- 1. Сложность задач
- 2. Чем определяется сложность задачи?Предметом вычислительной техники являются
- 3. Измерение сложности задачи
- 4. Способы определения сложности задачиПусть временная сложность задачи
- 5. Алгоритма сортировки слиянием и его сложностьЭтот алгоритм
- 6. Сложность алгоритма сортировки слияниемОбщее количество сравнений, которые
- 7. Полиномиальные и не полиномиальные задачи Задача называется полиномиальной
- 8. NP-задачиЕсли набор команд не является алгоритмом в
- 9. Задача, которая может быть решена за полиномиальное
- 10. ЗаключениеТаким образом, задачи могут быть разрешимыми (имеющими
- 11. Графическое представление классификации задач
- 12. Скачать презентанцию
Чем определяется сложность задачи?Предметом вычислительной техники являются задачи, которые умеют решать машины. Решения этих задач формулируются в виде алгоритмов. Таким образом, сложность задачи определяется свойствами алгоритмов, решающих ее. Точнее, сложность простейшего
Слайды и текст этой презентации
Слайд 2Чем определяется сложность задачи?
Предметом вычислительной техники являются задачи, которые умеют
Слайд 4Способы определения сложности задачи
Пусть временная сложность задачи равна Θ(f(n)), где
f(n) — это некоторая математическая функция от n. То есть
временная сложность задачи определяется как временная сложность ее наилучшего решения. В ситуациях, когда невозможно определить лучшее решение, для обозначения того, что нам известно о сложности задачи, применяется О-представление. Говоря, что задача принадлежит О(f(n)), мы имеем в виду, что для нее есть решение со сложностью Θ(f(n)), но, возможно, существуют и более хорошие решения.Слайд 5Алгоритма сортировки слиянием и его сложность
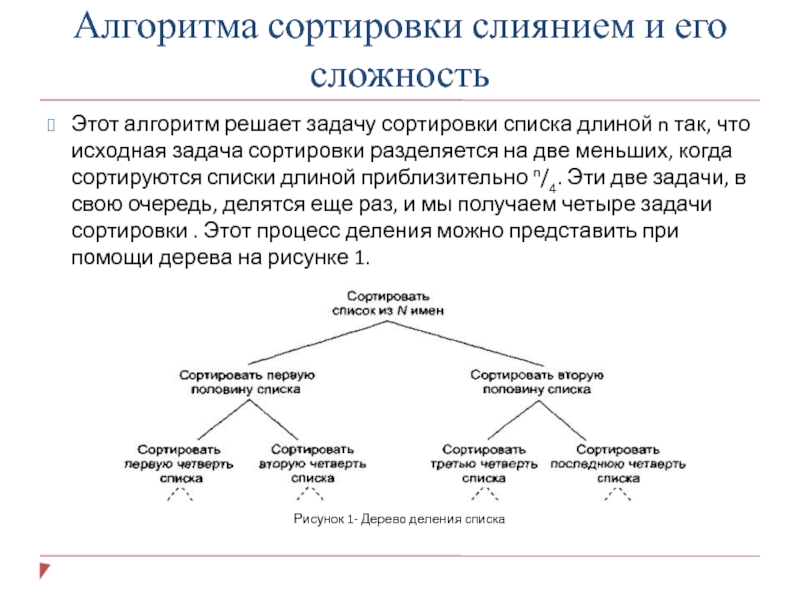
Этот алгоритм решает задачу сортировки
списка длиной n так, что исходная задача сортировки разделяется на
две меньших, когда сортируются списки длиной приблизительно n/4. Эти две задачи, в свою очередь, делятся еще раз, и мы получаем четыре задачи сортировки . Этот процесс деления можно представить при помощи дерева на рисунке 1.Рисунок 1- Дерево деления списка
Слайд 6Сложность алгоритма сортировки слиянием
Общее количество сравнений, которые выполняет алгоритм сортировки
слиянием при сортировке списка длиной n, получается умножением количества сравнений
на каждом уровне на количество уровней, на которых требуются сравнения. Мы делаем вывод, что оно не превышает n [lg n]. Т.е. алгоритм сортировки слиянием принадлежит О(n lg n). Учитывая тот факт, что сложность задачи сортировки равна Θ(n lg n), можно утверждать, что алгоритм сортировки слиянием является оптимальным решением задачи сортировки в отличии, например, от алгоритма сортировки вставкой, который принадлежит О(n2).Слайд 7Полиномиальные и не полиномиальные задачи
Задача называется полиномиальной (polynomial problem), если
она принадлежит О(f(n)), где f(n) - это полином (многочлен), или
это выражение ограничено полиномом. Набор всех полиномиальных задач обозначается Р.Поиск задач, принадлежащих Р, является одной из главных проблем вычислительной техники, так как он тесно связан с вопросами о том, существует ли для задач практическое решение. То, что теоретически разрешаемые проблемы, не принадлежащие Р, имеют огромную временную сложность, заставляет признать, что их невозможно решить с практической точки зрения. Ученые, занимающиеся вычислительной техникой, называют такие задачи трудно разрешимыми. В свою очередь, задачи, для которых существуют практические решения, содержатся в Р. Поэтому понимание границ класса Р стало важной областью исследований вычислительной техники.